2 Introduction to Pyomo

2.1 What is Pyomo?

Pyomo, or the Python Optimization Modelling Objects software, is an open-source package built for the Python scripting language. With Pyomo, the user can define abstract and concrete optimization problems to be solved by standard open-source and commercial solvers, such as Gurobi, IBM’s CPLEX and GLPK.

Pyomo shares its capabilities with other algebraic modelling languages, such as AMPL, GAMS and AIMMS, while taking advantage of Python’s powerful libraries (Pandas, Numpy, Matplotlib, etc) and the language’s object-oriented nature. Together with the Coopr software library, Pyomo also integrates IBM’s COIN-OR open-source initiative for operations research software [1].

2.2 What is a Linear Program?

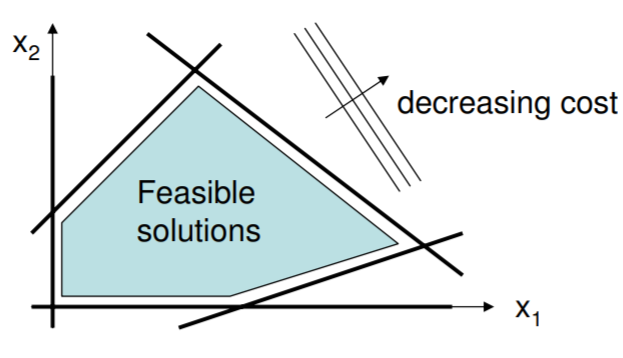
Linear programs are computer programs that employ optimization techniques to maximize, or to minimize a linear function. Typically, a linear optimization of an objective function is subject to one or more constraining functions. These constraints together bound the solution space of the problem, which is the graphical space that contains all feasible variable solutions to the problem

Linear programming theory is part of the operations research academic field and is extensively used in different industries and applications to solve different kinds of problems, such as profit maximization in businesses, shadow-price calculations in economics and the limit analysis of planar trusses in civil engineering [2]. In the case of this project, linear programming is extremely useful for finding the minimum cost of the implementation of renewable energy technologies in contrast with the currently available energy system in place in British Columbia.

2.3 Motivation: why choose Pyomo?

The MathProg modelling language is simple and objective for writing linear programs, which typically consist of a few component declarations:

Decision variables
Target (objective) function
Constraints
Data (model parameters)

The drawback for MathProg as a programming language, however, is its learning curve is attached directly to the understanding of linear optimization and the crude mathematics that describes linear problems in operations research. Pyomo allows us to achieve the same results from a linear problem by using a scripting language that does not require a deep understanding of operations research.

Pyomo diverges from MathProg by keeping a language that likens spoken English, while still meeting the goals of any modelling language (separation of model declarations from model data and keeping a concise problem definition). By taking advantage of Python’s readily available and powerful libraries for mathematical operations [3], such as Numpy, Pandas, Matplotlib and many others, Pyomo may also host a complex workflow that is otherwise hard to construct using MathProg. Furthermore, the use o Python as a modelling language can encourage a larger community of engineers and researchers to engage with the model development process, as Pyomo is open-source and Python is ranked as StackOverflow’s fourth most commonly used language for data analysis.

2.4 How to use Pyomo?

2.4.1 Installation

In order to use Pyomo for modelling energy systems, one will need to install the following programs and libraries into their machine:

Anaconda Python: latest Python version should work for Pyomo models, but you can change the distribution version after installation. Download your individual toolkit here
Create an Anaconda environment: after downloading Anaconda, open the Anaconda Prompt and create an environment to run your model.

To create an environment run the following command: conda create --name myenv python=3.6 (this will tell Anaconda to install Python v3.6 into the environment)
To install Python packages into your newly created environment, use the pip command: pip install pyomo (this installs Pyomo into the environment) after you activate it

To run your newly created environment, use the command conda activate myenv
The Python installation comes with some basic preinstalled libraries, but you may also wish to install other packages, such as Pandas (pip install pandas), or Numpy (pip install numpy)
Install the solvers to solve the linear problems.

To install GLPK on Windows, you can follow this tutorial by OSeMOSYS creators at the KTH Royal Institute of Technology
If you wish to install IBM’s CPLEX, you can follow their tutorial installation
Other commercial and open-source solvers are available as well, such as Gurobi, CBC and IPOPT

2.4.2 Modelling components

Pyomo models take advantage of Python’s object-oriented nature to assist the programmer when creating optimization models. Model objects are Python classes and as such contain many internal functions that can take arguments to construct the component [4]. The main components of any Pyomo model are:

Parameters
Sets
Variables
Objective functions
Constraints

The model components in Pyomo are supported by most Algebraic Modeling Languages (AMLs) [5], this way a Pyomo model can take in data from files in AML / AMPL data formats as input to construct the model instances. To illustrate the behavior of components inside a model, we can use a simple illustration: an optimization model is comprised of different equations, where at least one is the objective function and the remaining (non-objective functions) are constraints to our problem of study. Inside each equation we will have the decision variables, called Variables in the Pyomo script, each of which is accompanied by a corresponding term, called a Parameter inside Pyomo.

In the example below, function f(x,y) is a two-dimensional multi-variable equation with variables x and y and parameters a, b and c. Each variable, in this case x and y are also indexed by indices i and j, respectively; inside the Pyomo model these indices would be called Sets.

2.4.3 Modelling examples: concrete X abstract

As it was previously mentioned, optimization models in Pyomo are implemented as Python objects (classes), which will contain the model’s components inside them. A Pyomo model can either be Concrete, or Abstract and the main difference between these two implementations is the construction process of the model when the Python script is run.

Pyomo Concrete Models are used to build models which receive input data to their Sets and Parameters as these components are declared, then Python will immediately create an instance of the model to be given to the solver. An Abstract Model, however, can assume a less strict form, where the engineer may declare model components without necessarily assigning their corresponding data values immediately, this way, the model can serve as a more generic version of the problem and can receive data from different sources after the model instance is created [5]. “Abstract models include additional components for managing the declaration of model data, as well as logic for data initialization and validation” [5].

To illustrate the difference between the Concrete and Abstract model options in Pyomo, let us look into the same example problem being implemented using these two different model types. The problem in question is taken from Operations Research: Models and Methods by Jensen & Bard and has been implemented as a Pyomo Concrete Model by professor Brent Austgen of the University of Texas Austin as part of a workshop on optimization tools in Python. You can watch his full lecture for a deeper dive into Pyomo and optimization tools. The Abstract Model implementation of the problem has been carried out by Cristiano Fernandes of IESVic and is available inside this GitHub repository.

The main difference between Concrete and Abstract models that is noticible between the given examples is what is called model instantiation, which is the procedure of creating a model instance that is passed to the solver in order to get a solution. An instance of a model component is the creation of that component in memory by Pyomo and its initialization to the appropriate value; this process occurs in unique ways between Concrete and Abstract models.

Concrete model components are created and initialized as they are added to the model object, but Abstract model components are treated as "empty boxes" by Pyomo until an instance of the problem is created by the user, that is, in Abstract models, equations and components take prescedence over data, allowing the programmer to test the model for different datasets without the need for multiple model instances to be created. To create an Abstractmodel instance, we can simply use the create_instance() method from Pyomo and pass the instance of the model to the solver

instance = model.create_instance() # create the abstract model instance
opt = SolverFactory('glpk') # choose solver to be used
final_result = opt.solve(instance, tee=True) # pass instance to solver and display results on screen

2.4.4 Data usage inside Pyomo models

2.4.4.1 AMPL data files and the `pyomo` command

As shown by the Abstract Model example, a Pyomo abstract model can accept data input from sources other than the script itself, which allows for a model design and development that is independent of having available data for testing. This data can be imported into the model through data commands in a data file, or through ModelData objects and even by using data manipulation libraries, such as Pandas for extracting information from spreadsheets.

Pyomo's data command files closely resemble AMPL's data commands, but are not identical to one another. The main commands in a data file are set, parameter and import, when data is not present in the data file, but rather contained in a separate CSV, or other types of files. Additionally, Pyomo provides the data and end commands, which do not serve a major role inside the data file, but allow for compatibility between Pyomo data files and AMPL scripts that define data commands.

More about using data files is available in chapter 6 of the Pyomo Optimization textbook [5]. An example of a typical Pyomo data file is found here. It is also interesting to note that AMPL-like data files are also sometimes used by MathProg models, although with some minor syntax differences to the data files used by Pyomo models, meaning one could safely translate data files from a MathProg model to be used by a Pyomo model.

The pyomo command is used to run the model from the command line and is able to accpet data files, then read their information and pass to the solver to apply to the model. Here is an example to illustrate its use: pyomo solve --solver=glpk my_model.py my_data.dat --summary. In this example, the following steps will take place after the command is executed:

pyomo solve: evoke pyomo from the command line and inform of a problem to be solved
--solver=glpk: pass the problem information to the chosen solver (model definitions and model data)
my_model.py: give the Pyomo model file with model definitions
my_data.dat: give the Pyomo data file with model data information

2.4.4.2 Using Pandas for data manipulation

One of the ways to initialize model parameters and sets in Pyomo is through the data processing library, Pandas. Pandas' data frames allow us to retrieve data from spreadsheets and treat them as a SQL table, or a Python dictionary. The correct manipulation of these data frames can facilitate the initialization process by parsing individual parts of a large spreadsheet one step at a time.

In our OSeMOSYS model, Pandas was employed to allow us to bypass data imports through other means, such as the ModelData functionality of Pyomo and to allow the model to run entirely from the IDE. Our function for data processing is shown below.

def Process_Data(data, component="set"): # Where data is a Pandas Data Frame
    data = data.to_dict('list') # Transform dataframe into dictionary of lists
    #print(data)
    included = data.pop('Included') # Get the 'Included' column as a separate list (alternative way of achieving this: list(data.values())[0] )
    value = list(data.values())[-1] # Get parameter values as a separate list
    if component == "set": # Initialize sets
        initializer = []
        for k in range(len(value)):
            if included[k] == "Yes":
                initializer.append(value[k])
    elif component == "parameter": # Initialize parameters
        initializer = {}
        sets = list(data.values())[0:-1]
        set_tuples = [tuple([i[j] for i in sets]) for j in range(len(sets[0]))] # Get sets indexing the parameter as tuples
        for k, i, j in zip(included, set_tuples, value):
            if(k == 'No'):
                continue
            if not math.isnan(j):
                initializer[i] = j
    return initializer

It is important to note that our data parsing function is application specific, that is, it serves the purpose of parsing the data in the format we are feeding into the model. If you have data provided from an outside source, then the data frames need to be carefully constructed to fit in the appropriate sets and parameters for your model.