1. 单调栈简介

单调栈（Monotone Stack）：一种特殊的栈。在栈的「先进后出」规则基础上，要求「从栈顶到栈底的元素是单调递增（或者单调递减）」。其中满足从栈顶到栈底的元素是单调递增的栈，叫做「单调递增栈」。满足从栈顶到栈底的元素是单调递减的栈，叫做「单调递减栈」。

注意：这里定义的顺序是从「栈顶」到「栈底」。有的文章里是反过来的。本文全文以「栈顶」到「栈底」的顺序为基准来描述单调栈。

1.1 单调递增栈

单调递增栈：只有比栈顶元素小的元素才能直接进栈，否则需要先将栈中比当前元素小的元素出栈，再将当前元素入栈。

这样就保证了：栈中保留的都是比当前入栈元素大的值，并且从栈顶到栈底的元素值是单调递增的。

单调递增栈的入栈、出栈过程如下：

假设当前进栈元素为 $x$，如果 $x$ 比栈顶元素小，则直接入栈。
否则从栈顶开始遍历栈中元素，把小于 $x$ 或者等于 $x$ 的元素弹出栈，直到遇到一个大于 $x$ 的元素为止，然后再把 $x$ 压入栈中。

下面我们以数组 $[2, 7, 5, 4, 6, 3, 4, 2]$ 为例，模拟一下「单调递增栈」的进栈、出栈过程。具体过程如下：

数组元素：$[2, 7, 5, 4, 6, 3, 4, 2]$，遍历顺序为从左到右。

第 i 步	待插入元素	操作	结果（左侧为栈底）	作用
1	2	2 入栈	[2]	元素 2 的左侧无比 2 大的元素
2	7	2 出栈，7 入栈	[7]	元素 7 的左侧无比 7 大的元素
3	5	5 入栈	[7, 5]	元素 5 的左侧第一个比 5 大的元素为：7
4	4	4 入栈	[7, 5, 4]	元素 4 的左侧第一个比 4 大的元素为：5
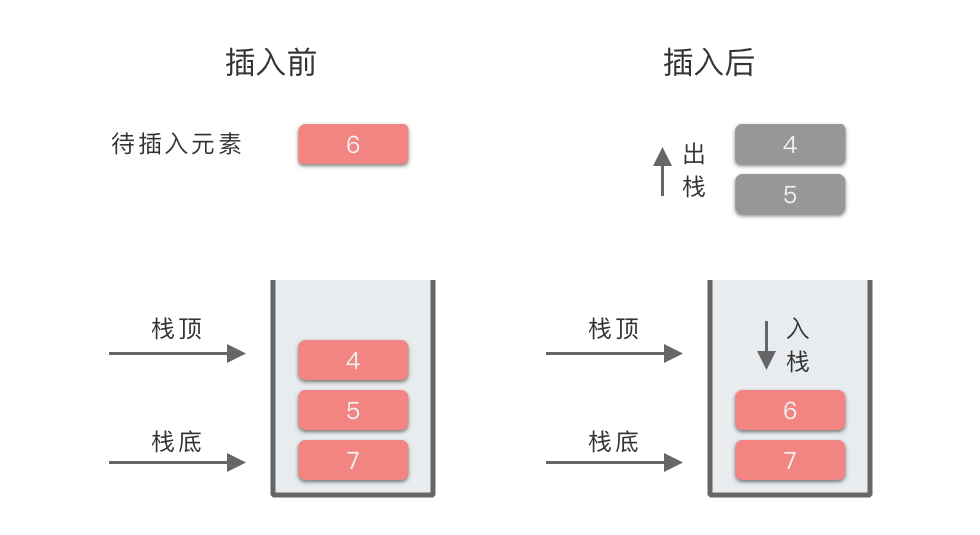
5	6	4 出栈，5 出栈，6 入栈	[7, 6]	元素 6 的左侧第一个比 6 大的元素为：7
6	3	3 入栈	[7, 6, 3]	元素 3 的左侧第一个比 3 大的元素为：6
7	4	3 出栈，4 入栈	[7, 6, 4]	元素 4 的左侧第一个比 4 大的元素为：6
8	2	2 入栈	[7, 6, 4, 2]	元素 2 的左侧第一个比 2 大的元素为：4

最终栈中元素为 $[7, 6, 4, 2]$。因为从栈顶（右端）到栈底（左侧）元素的顺序为 $2, 4, 6, 7$，满足递增关系，所以这是一个单调递增栈。

我们以上述过程第 5 步为例，所对应的图示过程为：

1.2 单调递减栈

单调递减栈：只有比栈顶元素大的元素才能直接进栈，否则需要先将栈中比当前元素大的元素出栈，再将当前元素入栈。

这样就保证了：栈中保留的都是比当前入栈元素小的值，并且从栈顶到栈底的元素值是单调递减的。

单调递减栈的入栈、出栈过程如下：

假设当前进栈元素为 $x$，如果 $x$ 比栈顶元素大，则直接入栈。
否则从栈顶开始遍历栈中元素，把大于 $x$ 或者等于 $x$ 的元素弹出栈，直到遇到一个小于 $x$ 的元素为止，然后再把 $x$ 压入栈中。

下面我们以数组 $[4, 3, 2, 5, 7, 4, 6, 8]$ 为例，模拟一下「单调递减栈」的进栈、出栈过程。具体过程如下：

数组元素：$[4, 3, 2, 5, 7, 4, 6, 8]$，遍历顺序为从左到右。

第 i 步	待插入元素	操作	结果（左侧为栈底）	作用
1	4	4 入栈	[4]	元素 4 的左侧无比 4 小的元素
2	3	4 出栈，3 入栈	[3]	元素 3 的左侧无比 3 小的元素
3	2	3 出栈，2 入栈	[2]	元素 2 的左侧无比 2 小的元素
4	5	5 入栈	[2, 5]	元素 5 的左侧第一个比 5 小的元素是：2
5	7	7 入栈	[2, 5, 7]	元素 7 的左侧第一个比 7 小的元素是：5
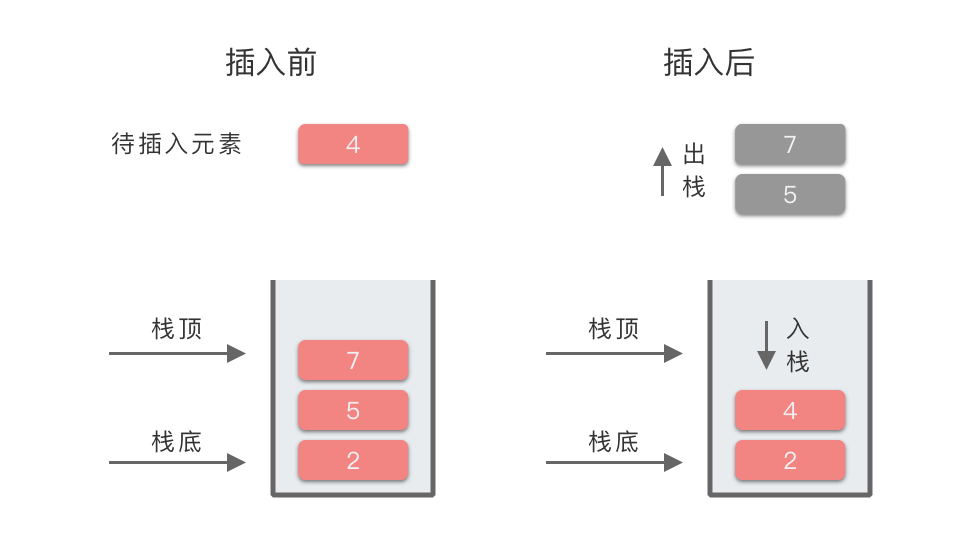
6	4	7 出栈，5 出栈，4 入栈	[2, 4]	元素 4 的左侧第一个比 4 小的元素是：2
7	6	6 入栈	[2, 4, 6]	元素 6 的左侧第一个比 6 小的元素是：4
8	8	8 入栈	[2, 4, 6, 8]	元素 8 的左侧第一个比 8 小的元素是：6

最终栈中元素为 $[2, 4, 6, 8]$。因为从栈顶（右端）到栈底（左侧）元素的顺序为 $8, 6, 4, 2$，满足递减关系，所以这是一个单调递减栈。

我们以上述过程第 6 步为例，所对应的图示过程为：

2. 单调栈适用场景

单调栈可以在时间复杂度为 $O(n)$ 的情况下，求解出某个元素左边或者右边第一个比它大或者小的元素。

所以单调栈一般用于解决一下几种问题：

寻找左侧第一个比当前元素大的元素。
寻找左侧第一个比当前元素小的元素。
寻找右侧第一个比当前元素大的元素。
寻找右侧第一个比当前元素小的元素。

下面分别说一下这几种问题的求解方法。

2.1 寻找左侧第一个比当前元素大的元素

从左到右遍历元素，构造单调递增栈（从栈顶到栈底递增）：
- 一个元素左侧第一个比它大的元素就是将其「插入单调递增栈」时的栈顶元素。
- 如果插入时的栈为空，则说明左侧不存在比当前元素大的元素。

2.2 寻找左侧第一个比当前元素小的元素

从左到右遍历元素，构造单调递减栈（从栈顶到栈底递减）：
- 一个元素左侧第一个比它小的元素就是将其「插入单调递减栈」时的栈顶元素。
- 如果插入时的栈为空，则说明左侧不存在比当前元素小的元素。

2.3 寻找右侧第一个比当前元素大的元素

从左到右遍历元素，构造单调递增栈（从栈顶到栈底递增）：
- 一个元素右侧第一个比它大的元素就是将其「弹出单调递增栈」时即将插入的元素。
- 如果该元素没有被弹出栈，则说明右侧不存在比当前元素大的元素。
从右到左遍历元素，构造单调递增栈（从栈顶到栈底递增）：
- 一个元素右侧第一个比它大的元素就是将其「插入单调递增栈」时的栈顶元素。
- 如果插入时的栈为空，则说明右侧不存在比当前元素大的元素。

2.4 寻找右侧第一个比当前元素小的元素

从左到右遍历元素，构造单调递减栈（从栈顶到栈底递减）：
- 一个元素右侧第一个比它小的元素就是将其「弹出单调递减栈」时即将插入的元素。
- 如果该元素没有被弹出栈，则说明右侧不存在比当前元素小的元素。
从右到左遍历元素，构造单调递减栈（从栈顶到栈底递减）：
- 一个元素右侧第一个比它小的元素就是将其「插入单调递减栈」时的栈顶元素。
- 如果插入时的栈为空，则说明右侧不存在比当前元素小的元素。

上边的分类解法有点绕口，可以简单记为以下条规则：

无论哪种题型，都建议从左到右遍历元素。
查找 「比当前元素大的元素」 就用 单调递增栈，查找 「比当前元素小的元素」 就用 单调递减栈。
从 「左侧」 查找就看 「插入栈」 时的栈顶元素，从 「右侧」 查找就看 「弹出栈」 时即将插入的元素。

3. 单调栈模板

以从左到右遍历元素为例，介绍一下构造单调递增栈和单调递减栈的模板。

3.1 单调递增栈模板

def monotoneIncreasingStack(nums):
    stack = []
    for num in nums:
        while stack and num >= stack[-1]:
            stack.pop()
        stack.append(num)

3.2 单调递减栈模板

def monotoneDecreasingStack(nums):
    stack = []
    for num in nums:
        while stack and num <= stack[-1]:
            stack.pop()
        stack.append(num)

4. 单调栈的应用

4.1 下一个更大元素 I

4.1.1 题目链接

0496. 下一个更大元素 I

4.1.2 题目大意

给定两个没有重复元素的数组 $nums1$ 和 $nums2$ ，其中 $nums1$ 是 $nums2$ 的子集。

要求：找出 $nums1$ 中每个元素在 $nums2$ 中的下一个比其大的值。

$nums1$ 中数字 $x$ 的下一个更大元素是指：$x$ 在 $nums2$ 中对应位置的右边的第一个比 $x$ 大的元素。如果不存在，对应位置输出 $-1$。

4.1.3 解题思路

第一种思路是根据题意直接暴力求解。遍历 $nums1$ 中的每一个元素。对于 $nums1$ 的每一个元素 $nums1[i]$，再遍历一遍 $nums2$，查找 $nums2$ 中对应位置右边第一个比 $nums1[i]$ 大的元素。这种解法的时间复杂度是 $O(n^2)$。

第二种思路是使用单调递增栈。因为 $nums1$ 是 $nums2$ 的子集，所以我们可以先遍历一遍 $nums2$，并构造单调递增栈，求出 $nums2$ 中每个元素右侧下一个更大的元素。然后将其存储到哈希表中。然后再遍历一遍 $nums1$，从哈希表中取出对应结果，存放到答案数组中。这种解法的时间复杂度是 $O(n)$。具体做法如下：

使用数组 $res$ 存放答案。使用 $stack$ 表示单调递增栈。使用哈希表 $num\underline{\hspace{0.5em}}map$ 用于存储 $nums2$ 中下一个比当前元素大的数值，映射关系为 当前元素值：下一个比当前元素大的数值。
遍历数组 $nums2$，对于当前元素：
- 如果当前元素值较小，则直接让当前元素值入栈。
- 如果当前元素值较大，则一直出栈，直到当前元素值小于栈顶元素。
  - 出栈时，出栈元素是第一个大于当前元素值的元素。则将其映射到 $num\underline{\hspace{0.5em}}map$ 中。
遍历完数组 $nums2$，建立好所有元素下一个更大元素的映射关系之后，再遍历数组 $nums1$。
从 $num\underline{\hspace{0.5em}}map$ 中取出对应的值，将其加入到答案数组中。
最终输出答案数组 $res$。

4.1.4 代码

class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        res = []
        stack = []
        num_map = dict()
        for num in nums2:
            while stack and num > stack[-1]:
                num_map[stack[-1]] = num
                stack.pop()
            stack.append(num)

        for num in nums1:
            res.append(num_map.get(num, -1))
        return res

4.2 每日温度

4.2.1 题目链接

739. 每日温度 - 力扣（LeetCode）

4.2.2 题目大意

描述：给定一个列表 $temperatures$，$temperatures[i]$ 表示第 $i$ 天的气温。

要求：输出一个列表，列表上每个位置代表「如果要观测到更高的气温，至少需要等待的天数」。如果之后的气温不再升高，则用 $0$ 来代替。

说明：

$1 \le temperatures.length \le 10^5$。
$30 \le temperatures[i] \le 100$。

示例：

输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]


输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]

4.2.3 解题思路

题目的意思实际上就是给定一个数组，每个位置上有整数值。对于每个位置，在该位置右侧找到第一个比当前元素更大的元素。求「该元素」与「右侧第一个比当前元素更大的元素」之间的距离，将所有距离保存为数组返回结果。

最简单的思路是对于每个温度值，向后依次进行搜索，找到比当前温度更高的值。

更好的方式使用「单调递增栈」，栈中保存元素的下标。

思路 1：单调栈

首先，将答案数组 $ans$ 全部赋值为 0。然后遍历数组每个位置元素。
如果栈为空，则将当前元素的下标入栈。
如果栈不为空，且当前数字大于栈顶元素对应数字，则栈顶元素出栈，并计算下标差。
此时当前元素就是栈顶元素的下一个更高值，将其下标差存入答案数组 $ans$ 中保存起来，判断栈顶元素。
直到当前数字小于或等于栈顶元素，则停止出栈，将当前元素下标入栈。
最后输出答案数组 $ans$。

思路 1：代码

class Solution:
    def dailyTemperatures(self, T: List[int]) -> List[int]:
        n = len(T)
        stack = []
        ans = [0 for _ in range(n)]
        for i in range(n):
            while stack and T[i] > T[stack[-1]]:
                index = stack.pop()
                ans[index] = (i-index)
            stack.append(i)
        return ans

思路 1：复杂度分析

时间复杂度：$O(n)$。
空间复杂度：$O(n)$。

参考资料

【博文】动画：什么是单调栈？_- 吴师兄学编程
【博文】单调栈 - OI Wiki
【博文】单调栈解题模板秒杀八道题 - lucifer 的网络博客
【博文】理解单调栈与单调队列 - Hopefully Sky 的博客

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

01.Monotone-Stack.md

01.Monotone-Stack.md

1. 单调栈简介

1.1 单调递增栈

1.2 单调递减栈

2. 单调栈适用场景

2.1 寻找左侧第一个比当前元素大的元素

2.2 寻找左侧第一个比当前元素小的元素

2.3 寻找右侧第一个比当前元素大的元素

2.4 寻找右侧第一个比当前元素小的元素

3. 单调栈模板

3.1 单调递增栈模板

3.2 单调递减栈模板

4. 单调栈的应用

4.1 下一个更大元素 I

4.1.1 题目链接

4.1.2 题目大意

4.1.3 解题思路

4.1.4 代码

4.2 每日温度

4.2.1 题目链接

4.2.2 题目大意

4.2.3 解题思路

思路 1：单调栈

思路 1：代码

思路 1：复杂度分析

参考资料

Files

01.Monotone-Stack.md

Latest commit

History

01.Monotone-Stack.md

File metadata and controls

1. 单调栈简介

1.1 单调递增栈

1.2 单调递减栈

2. 单调栈适用场景

2.1 寻找左侧第一个比当前元素大的元素

2.2 寻找左侧第一个比当前元素小的元素

2.3 寻找右侧第一个比当前元素大的元素

2.4 寻找右侧第一个比当前元素小的元素

3. 单调栈模板

3.1 单调递增栈模板

3.2 单调递减栈模板

4. 单调栈的应用

4.1 下一个更大元素 I

4.1.1 题目链接

4.1.2 题目大意

4.1.3 解题思路

4.1.4 代码

4.2 每日温度

4.2.1 题目链接

4.2.2 题目大意

4.2.3 解题思路

思路 1：单调栈

思路 1：代码

思路 1：复杂度分析

参考资料