Skip to content

Latest commit

 

History

History
197 lines (148 loc) · 8.69 KB

01.Binary-Search-Tree.md

File metadata and controls

197 lines (148 loc) · 8.69 KB
Raw

1. 二叉搜索树简介

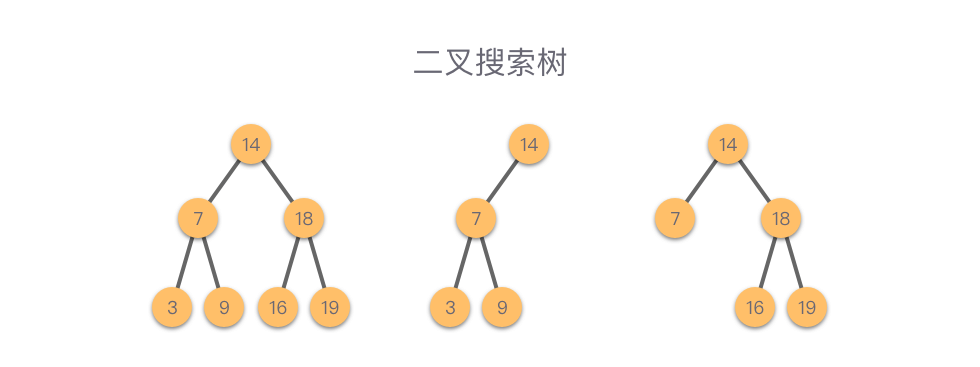
二叉搜索树（Binary Search Tree）：也叫做二叉查找树、有序二叉树或者排序二叉树。是指一棵空树或者具有下列性质的二叉树：

  • 如果任意节点的左子树不为空，则左子树上所有节点的值均小于它的根节点的值。
  • 如果任意节点的右子树不为空，则右子树上所有节点的值均大于它的根节点的值。
  • 任意节点的左子树、右子树均为二叉搜索树。

如图所示，这 $3$ 棵树都是二叉搜索树。

img

二叉树具有一个特性，即：左子树的节点值 < 根节点值 < 右子树的节点值。

根据这个特性，如果我们以中序遍历的方式遍历整个二叉搜索树时，会得到一个递增序列。例如，一棵二叉搜索树的中序遍历序列如下图所示。

2. 二叉搜索树的查找

二叉搜索树的查找：在二叉搜索树中查找值为 $val$ 的节点。

2.1 二叉搜索树的查找算法步骤

按照二叉搜索树的定义，在进行元素查找时，我们只需要根据情况判断需要往左还是往右走。这样，每次根据情况判断都会缩小查找范围，从而提高查找效率。二叉树的查找步骤如下：

  1. 如果二叉搜索树为空，则查找失败，结束查找，并返回空指针节点 $None$。
  2. 如果二叉搜索树不为空，则将要查找的值 $val$ 与二叉搜索树根节点的值 $root.val$ 进行比较：
    1. 如果 $val == root.val$，则查找成功，结束查找，返回被查找到的节点。
    2. 如果 $val &lt; root.val$，则递归查找左子树。
    3. 如果 $val &gt; root.val$，则递归查找右子树。

2.2 二叉搜索树的查找代码实现

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        if not root:
            return None
        
        if val == root.val:
            return root
        elif val < root.val:
            return self.searchBST(root.left, val)
        else:
            return self.searchBST(root.right, val)

2.3 二叉搜索树的查找算法分析

  • 二叉搜索树的查找时间复杂度和树的形态有关。
  • 在最好情况下，二叉搜索树的形态与二分查找的判定树相似。每次查找都可以所辖一半搜索范围。查找路径最多从根节点到叶子节点，比较次数最多为树的高度 $\log_2 n$。在最好情况下查找的时间复杂度为 $O(\log_2 n)$。
  • 在最坏情况下，二叉搜索树的形态为单支树，即只有左子树或者只有右子树。每次查找的搜索范围都缩小为 $n - 1$，退化为顺序查找，在最坏情况下时间复杂度为 $O(n)$。
  • 在平均情况下，二叉搜索树的平均查找长度为 $ASL = [(n + 1) / n] * /log_2(n+1) - 1$。所以二分搜索树的查找平均时间复杂度为 $O(log_2 n)$。

3. 二叉搜索树的插入

二叉搜索树的插入：在二叉搜索树中插入一个值为 $val$ 的节点（假设当前二叉搜索树中不存在值为 $val$ 的节点）。

3.1 二叉搜索树的插入算法步骤

二叉搜索树的插入操作与二叉树的查找操作过程类似，具体步骤如下：

  1. 如果二叉搜索树为空，则创建一个值为 $val$ 的节点，并将其作为二叉搜索树的根节点。
  2. 如果二叉搜索树不为空，则将待插入的值 $val$ 与二叉搜索树根节点的值 $root.val$ 进行比较：
    1. 如果 $val &lt; root.val$，则递归将值为 $val$ 的节点插入到左子树中。
    2. 如果 $val &gt; root.val$，则递归将值为 $val$ 的节点插入到右子树中。

注意：二叉搜索树不允许存在重复节点，否则将违反其定义。因此，如果带插入节点在树中已存在，则不执行插入操作，直接返回。

3.2 二叉搜索树的插入代码实现

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
        if root == None:
            return TreeNode(val)

        if val < root.val:
            root.left = self.insertIntoBST(root.left, val)
        if val > root.val:
            root.right = self.insertIntoBST(root.right, val)
        return root

4. 二叉搜索树的创建

二叉搜索树的创建：根据数组序列中的元素值，建立一棵二叉搜索树。

4.1 二叉搜索树的创建算法步骤

二叉搜索树的创建操作是从空树开始，按照给定数组元素的值，依次进行二叉搜索树的插入操作，最终得到一棵二叉搜索树。具体算法步骤如下：

  1. 初始化二叉搜索树为空树。
  2. 遍历数组元素，将数组元素值 $nums[i]$ 依次插入到二叉搜索树中。
  3. 将数组中全部元素值插入到二叉搜索树中之后，返回二叉搜索树的根节点。

4.2 二叉搜索树的创建代码实现

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
        if root == None:
            return TreeNode(val)

        if val < root.val:
            root.left = self.insertIntoBST(root.left, val)
        if val > root.val:
            root.right = self.insertIntoBST(root.right, val)
        return root
    def buildBST(self, nums) -> TreeNode:
        root = TreeNode(val)
        for num in nums:
            self.insertIntoBST(root, num)
        return root

5. 二叉搜索树的删除

二叉搜索树的删除：在二叉搜索树中删除值为 $val$ 的节点。

5.1 二叉搜索树的删除算法步骤

在二叉搜索树中删除元素，首先要找到待删除节点，然后执行删除操作。根据待删除节点所在位置的不同，可以分为 $3$ 种情况：

  1. 被删除节点的左子树为空。则令其右子树代替被删除节点的位置。
  2. 被删除节点的右子树为空。则令其左子树代替被删除节点的位置。
  3. 被删除节点的左右子树均不为空，则根据二叉搜索树的中序遍历有序性，删除该节点时，可以使用其直接前驱（或直接后继）代替被删除节点的位置。
  • 直接前驱：在中序遍历中，节点 $p$ 的直接前驱为其左子树的最右侧的叶子节点。
  • 直接后继：在中序遍历中，节点 $p$ 的直接后继为其右子树的最左侧的叶子节点。

二叉搜索树的删除算法步骤如下：

  1. 如果当前节点为空，则返回当前节点。
  2. 如果当前节点值大于 $val$，则递归去左子树中搜索并删除，此时 $root.left$ 也要跟着递归更新。
  3. 如果当前节点值小于 $val$，则递归去右子树中搜索并删除，此时 $root.right$ 也要跟着递归更新。
  4. 如果当前节点值等于 $val$，则该节点就是待删除节点。
    1. 如果当前节点的左子树为空，则删除该节点之后，则右子树代替当前节点位置，返回右子树。
    2. 如果当前节点的右子树为空，则删除该节点之后，则左子树代替当前节点位置，返回左子树。
    3. 如果当前节点的左右子树都有，则将左子树转移到右子树最左侧的叶子节点位置上，然后右子树代替当前节点位置。

5.2 二叉搜索树的删除代码实现

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def deleteNode(self, root: TreeNode, val: int) -> TreeNode:
        if not root:
            return root

        if root.val > val:
            root.left = self.deleteNode(root.left, val)
            return root
        elif root.val < val:
            root.right = self.deleteNode(root.right, val)
            return root
        else:
            if not root.left:
                return root.right
            elif not root.right:
                return root.left
            else:
                curr = root.right
                while curr.left:
                    curr = curr.left
                curr.left = root.left
                return root.right

参考资料

  • 【书籍】算法训练营 陈小玉 著
  • 【书籍】算法竞赛入门经典：训练指南 - 刘汝佳，陈锋 著
  • 【书籍】算法竞赛进阶指南 - 李煜东 著
  • 【博文】7.4 二叉搜索树 - Hello 算法