Skip to content

Latest commit

 

History

History
186 lines (104 loc) · 5.63 KB

Discrete_Mathematics.md

File metadata and controls

186 lines (104 loc) · 5.63 KB

Discrete Mathematics

컴퓨터를 위한 수학


Discrete Mathematics provides a common forum for significant research in many areas of discrete mathematics and combinatorics.



이산수학 개요

참과 거짓으로 살펴보는 컴퓨터 수학


왜 배워야 하는가?

  • 이산수학이란 불연속적인 숫자를 다루는 수학

  • 컴퓨터에서는 내부적으로 0과 1만을 다루는데 그러한 불연속적인 데이터의 흐름을 다루기에 적합한 수학적 사고를 배양하는데 필수적인 강의다

  • 이산수학에서 다루는 내용이 자료구조, 알고리즘 등의 베이스가 되어 전체적인 Computational Thinking을 길러준다


이산수학은 컴퓨터 과학의 베이스 학문이다!



명제와 연산자


명제 (proposition)

진실 혹은 거짓

  • 참(True)이나 거짓(False)으로 진리를 구분할 수 있는 문장
  • 명제는 0 또는 1만을 가지는 컴퓨터 메모리처럼 항상 참과 거짓 둘 중 하나의 값만을 가진다
  • 여러개의 명제를 조합할 수도 있다
    • 합성 명제 (Compound Proposition)

논리 연산자 (logical operator)

연산자는 명제를 연산하기 위한 도구이며, 이산수학의 기본 연산자로는 6가지가 있다


image-20200423194638742



  1. Not

    • 뒤에 오는 명제에 대해 참 <-> 거짓을 바꾸어줌

  2. And

    • 논리곱

    • 두 개의 명제를 묶을 때 사용

    • 둘 다 참일때만 참

      • 한 개라도 거짓이면 거짓

  3. Or

    • 논리합

    • 둘 중 하나라도 참이면 참

  4. Exclusive or

    • 배타적 논리합
      • 서로를 배제한다
    • 둘 중 단 한 개만 참인 경우 참

  5. Implication (함축)

    • 조건 명제 (Conditional Proposition)
      • 어떠한 조건일때, 이런 결과가 나온다
        • 조건과 결과에 따른 흐름을 표현할 때 사용
      • 원인이 되는 명제와 결과가 되는 명제가 존재하는 명제
    • p -> q
      • p가 True, q가 False일 때에만 조건 명제는 False 값을 반환

  6. Biconditional

    • 쌍방 조건 명제
    • 두 값이 서로 일치할 때에만 쌍방 조건 명제는 True 값을 반환함


역, 이 , 대우 (converse, inverse, contrapositive)


진리표 (Truth-Table)

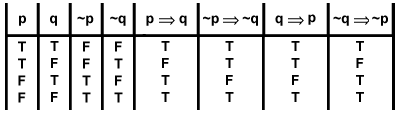
  • 각 명제 사이의 관계식의 진릿값을 보여주는 표
  • 아무리 복잡한 합성 명제 라도 진리표를 통해 풀어낼 수 있다!

img



역, 이, 대우


image-20200424040719609


  • 조건 명제 (Conditional Proposition)에서 사용함
  • 하나의 명제를 변형해 표헌함
  • 증명에 도움을 준다
  • 증명하기 어려운 명제는 대우를 이용해 증명할 수 있음
    • 어떤 명제의 대우가 참인 경우, 본 명제 또한 참이기 때문!



동치 (equivalent)

두 개의 명제가 서로 같은 진리값을 갖고 있을 때


동치의 의미

  • 동치란 '논리적으로 일치한다' 는 의미
  • 같은 의미를 가진 더 쉬운 명제를 발견하는 데 사용
  • 동치 법칙에는 다양한 종류가 있음

동치 법칙을 이용해 증명하기

복잡해 보이는 합셩 명제 (compositional proposition)도 동치 법칙을 이용해 간단한 명제로 바꿀 수 있다!


\begin{tabular}{ ||c||c|| } \hline Equivalence & Name of Identity\\ \hline \hline p\wedge T \equiv p & Identity Laws\\ p\vee F \equiv p & \\ \hline p\wedge F \equiv F & Domination Laws\\ p\vee T \equiv T & \\ \hline p\wedge p \equiv p & Idempotent Laws\\ p\vee p \equiv p & \\ \hline \neg(\neg p) \equiv p & Double Negation Law\\ \hline p\wedge q \equiv q\wedge p & Commutative Laws\\ p\vee q \equiv q\vee p & \\ \hline (p\wedge q) \wedge r\equiv p\wedge (q \wedge r) & Associative Laws\\ (p\vee q) \vee r\equiv p\vee (q \vee r) & \\ \hline p\wedge (q \vee r)\equiv (p\wedge q)\vee (p\wedge r) & Ditributive Laws\\ p\vee (q \wedge r)\equiv (p\vee q)\wedge (p\vee r) & \\ \hline \hline \neg(p\wedge q) \equiv \neg p \vee \neg q & De Morgan's Laws\\ \neg(p\vee q) \equiv \neg p \wedge \neg q & \\ \hline p\wedge (p \vee q)\equiv p & Absorption Laws\\ p\vee (p \wedge q)\equiv p & \\ \hline p\wedge \neg p \equiv F & Negation Laws\\ p\vee \neg p \equiv T & \\ \hline \end{tabular}


  • 항등 법칙

    • 비교 대상의 True/False 여부에 관계 없이 p 값을 가진다

  • 지배 법칙

    • 비교 대상에 따라 결과가 지배적으로 결정된다

  • 드 모르간의 법칙

    • p and q 일 때, not을 붙이면 각각 ~p or ~q 가 된다
    • 반대로 p or q에 not을 붙이면 각각 ~p and ~q가 된다

  • 흡수 법칙

    • 바깥에 있는 값이 강력해서 괄호 () 안의 여부에 상관 없이 바깥의 결과에 흡수된다

  • 부정 법칙

    • 둘 중 하나가 not 일 때 and 연산이면 True, or 연산이면 False 반환

  • 함축 법칙

    • p -> q <-> ~q or q