breadth-first-search.md

Breadth-first Search

Breadth-first search (or BFS) is a form of graph traversal that starts at some vertex i and visits all of i's neighbors. It then visits all of the neighbors of i's neighbors. This process keeps going until there are no more vertices left to visit.

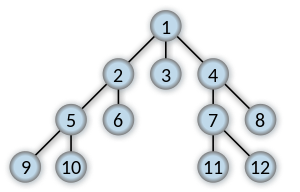
Imagine a "family tree", like one shown in the picture above. BFS will visit all vertices of the same level before moving on to the next level.

We start by visiting vertex 1.

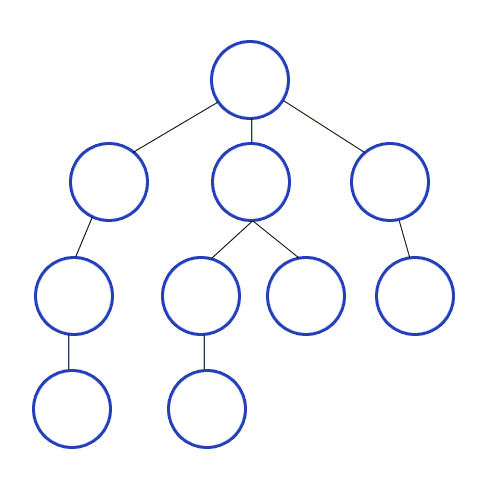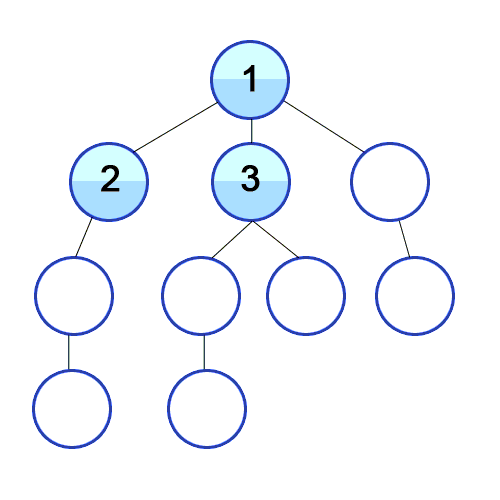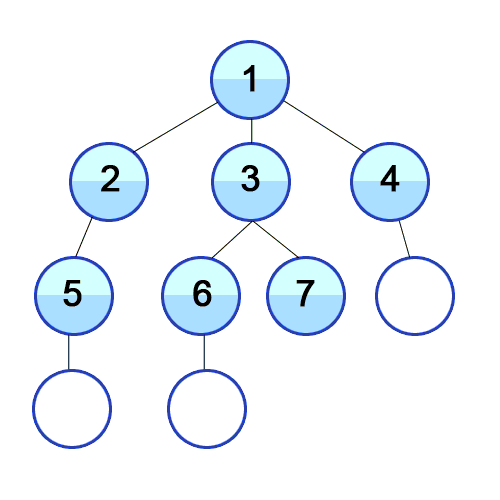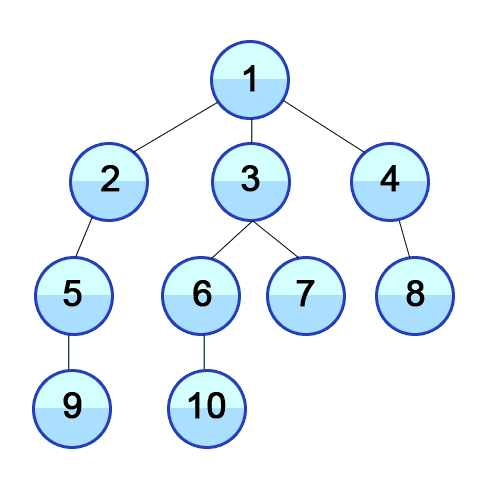
Then, we visit all of 1's neighbors: 2, 3, 4

Then, we visit all of 1's neighbors' neighbors: 5, 6, 7, 8

Finally, we visit all of their neighbors: 9, 10, 11, 12

Above is another visual representation of the BFS process starting from the top vertex.

Coding BFS

We need to use some data structure that will allow us to visit vertices "level-by-level", that is, visit every vertex at level j before we visit any vertex at level j+1.

In order to do this, we will be using a Queue since it follows the "first in, first out" ordering; this means if we put all the vertices at level j into the queue before the vertices at level j+1, we are guaranteed to visit the lower level vertices first.

Below are the steps to follow for BFS:

1. Push the root vertex onto the queue
2. Pop the queue to get the current vertex
3. For each unvisited neighbor of the current vertex, mark them as visited and push them onto the queue
4. Go back to step 2 until the queue is empty

// Initialize the queue
Queue<Integer> queue = new LinkedList<Integer>(); 

// This array will tell us if we have visited a vertex
boolean[] visited = new boolean[ N ];               

// Push the root vertex onto the queue
queue.add( rootVertex );

// While there is a vertex still in the queue...
while ( !queue.isEmpty() )
{
    // Get the current vertex
    Integer current = queue.remove();     
    // Get the current vertex's neighbors
    ArrayList<Integer> neighbors = graph[ current ];
    
    // For each of the current vertex's neighbors...
    foreach ( Integer neighbor : neighbors )
    {
        // If we haven't visited the neighbor...
        if ( !visited[ neighbor ] )
        {
            // Add the neighbor to the queue
            queue.add( neighbor );
            // Mark the neighbor as visited
            visited[ neighbor ] = true;
        }
    }
}