| marp | paginate | backgroundColor | title | description | author | keywords | style |
|---|---|---|---|---|---|---|---|
true |
true |
Neutronics Workshop |
Presentation slides for the fusion energy neutronics workshop |
Jonathan Shimwell |
fusion,neutronics,neutron,photon,radiation,simulation,openmc,dagmc |
.columns {
display: grid;
grid-template-columns: repeat(2, minmax(0, 1fr));
gap: 1rem;
},
.columns3 {
display: grid;
grid-template-columns: repeat(3, minmax(0, 1fr));
gap: 1rem;
},
h1 {
text-align: center
}
|
- Radioactivity - Neutrons activate material, making it radioactive leading to handling and waste storage requirements.
- Hazardous - Neutrons are Hazardous to health and shielded will be needed to protect the workforce.
- Produce fuel - Neutrons will be needed to convert lithium into tritium to fuel the reactor.
- Electricity - 80% of the energy release by each DT reaction is transferred to the neutron.
- Structural integrity - Neutrons cause damage to materials such as embrittlement, swelling, change conductivity …
- Diagnose - Neutrons are an important method of measuring a variety of plasma parameters (e.g. Q value).
-
Neutron and Photon interaction cross sections
-
Material creation
-
Particle sources
-
Constructive Solid Geometry (CSG)
-
Tallies (heat, tritium breeding ratio, damage, flux)
-
Neutron activation
-
🐋 Install Docker
-
🔽 Download the docker image
-
🏃Run the docker image
-
🔗 Navigate to the URL in the terminal
Detailed instructions are on GitHub
Install single package (Docker) and avoid installing a few hundred packages.
- Portable
- Reproducible
- Security
- Isolation
- Deployable
-
Collection of Jupyter notebooks
-
Separate task folder for each topic
-
Learning outcomes for each task
-
Simulation outputs include:
- numbers
- graphs
- images
- 3D visualization.
- Increasing adoption in fusion
- Supportive community
- GitHub repository
- Permissive license (MIT)
- Python API, C++ backend
- Scales to 100,000+ cores
- CPU and GPU version
- Online documentation
- Excellent fusion specific workshops
-
Run the docker image
docker run -p 8888:8888 ghcr.io/fusion-energy/neutronics-workshop -
Double click on the
half-day-workshopfolder circled in red.
- 9.00 Introduction presentation
- 9.10 Plotting cross sections
- task_01_isotope_xs_plot
- task_02_element_xs_plot
- task_03_material_xs_plot
- 9.40 Making materials
- task_04_example_materials_from_isotopes
- task_05_example_materials_from_elements
- 9.55 Geometry
- task_06_simple_csg_geometry
- 10.15 Break ☕
- 10.30 Plotting particles
- task_07_point_source_plots
- task_08_ring_source
- task_09_plasma_source_plots
- 11.05 Tritium Breeding Ratio (TBR)
- task_10_example_tritium_production
- 11.15 Damage (DPA)
- task_11_find_dpa
- 11:30 Break ☕
- 11:45 neutron photon spectra
- task_12_example_neutron_spectra_on_cell
- task_13_example_photon_spectra
- 12.15 mesh tallies
- task_14_example_2d_regular_mesh_tallies
- 12.30 activation
- task_15_full_pulse_schedule
- 12.45 Putting it all together
- task_16_optimal_design
-
Probability of interaction is characterised by the microscopic cross-section (σ). It is the effective size of the nucleus.
-
Cross section data is key to the neutronics workflow and provide us with the likelihood of a particular interaction.
-
Cross sections can be measured experimentally with monoenergetic neutrons.
Availability of experimental data varies for different reactions and different isotopes.
Typically the experimental data is then interpreted to create evaluation libraries, such as ENDF, JEFF, JENDL, CENDL.
Source IAEA nuclear data services
Cross section evaluations exist for:
- different nuclides
- different interactions.
A list of reactions available in OpenMC is here
For example:
- Be9(n,2n)2He would be a neutron interaction with beryllium 9 which results in 2 neutrons and 2 helium nuclei.
- Li6(n,Xt) would be a neutron interaction with lithium 6 nuclei which results in a tritium and X is a wildcard.
- The reaction rate (
$RR$ ) can be found by knowing the number of neutrons per unit volume ($n$ ), the velocity of neutrons ($v$ ), the material density ($p$ ), Avogadro's number ($N_{a}$ ), the microscopic cross section at the neutron energy ($\sigma_{e}$ ) and the atomic weight of the material ($M$ ). - This reduces down to the neutron flux (
$\phi$ ), nuclide number density ($N_{d}$ ) and microscopic cross section$\sigma_{e}$ . - This can be reduced one more stage by making use of the Macroscopic cross section (
$\Sigma_{e}$ ).
Neutronics codes require the isotopes and the number density.
This can be provided with different combinations of density units, isotope/element concentration and weight or atom fractions.
Simple material construction from nuclides.
mat2 = openmc.Material()
mat2.add_nuclide('Li6', 0.0759*2)
mat2.add_nuclide('Li7', 0.9241*2)
mat2.add_nuclide('O16', 0.9976206)
mat2.add_nuclide('O17', 0.000379)
mat2.add_nuclide('O18', 0.0020004)
mat2.set_density('g/cm3', 2.01)Simpler material construction from elements.
import openmc
mat1 = openmc.Material()
mat1.add_element('H', 2)
mat1.add_element('O', 1)
mat1.set_density('g/cm3', 2.01)Simple enriched material construction from elements.
import openmc
mat1 = openmc.Material()
mat1.add_element('Li', 4, enrichment_target='Li6', enrichment=60)
mat1.add_element('Si', 1)
mat1.add_element('O', 4)
mat1.set_density('g/cm3', 2.01)The simplest geometry is a single surface and a cell defined as below (-) that surface.
import openmc
surface_sphere = openmc.Sphere(r=10.0)
region_inside_sphere = -surface_sphere
cell_sphere = openmc.Cell(region=region_inside_sphere)
cell_sphere.fill = steelCells can also be constrained by multiple surfaces. This example is above (+) one surface and (&) below (-) another
import openmc
surf_sphere1 = openmc.Sphere(r=10.0)
surf_sphere2 = openmc.Sphere(r=20.0)
between_spheres = +surf_sphere1 & -surf_sphere2
cell_between = openmc.Cell(region= between_spheres)
cell_sphere.fill = steelThe outer most surface of the model should have a boundary_type set to "vacuum" to indicate that neutrons should not be tracked beyond this surface.
import openmc
surf_sphere = openmc.Sphere(r=10.0, boundary_type="vacuum")
between_spheres = -surf_sphere
cell_between = openmc.Cell(region= between_spheres) Constructive Solid Geometry (CSG) implementation in OpenMC has the following surface types.
- XPlane, YPlane, ZPlane, Plane
- XCylinder, YCylinder, ZCylinder
- Sphere
- XCone, YCone, ZCone,
- Quadric
- XTorus, YTorus, ZTorus
 Image source Paramak
Image source Paramak
OpenMC also supports:
- boolean operations like union, intersection and complement.
- rotations and translations
- nested geometry with universes
- different surface types (e.g reflective for sector model)
For more complex 3D geometry DAGMC can be used which makes use of a meshed geometry to transport particles.
Neutron and photon sources have distributions for:
- space
- energy
- direction
Visualization of the source term helps check the simulation is correct
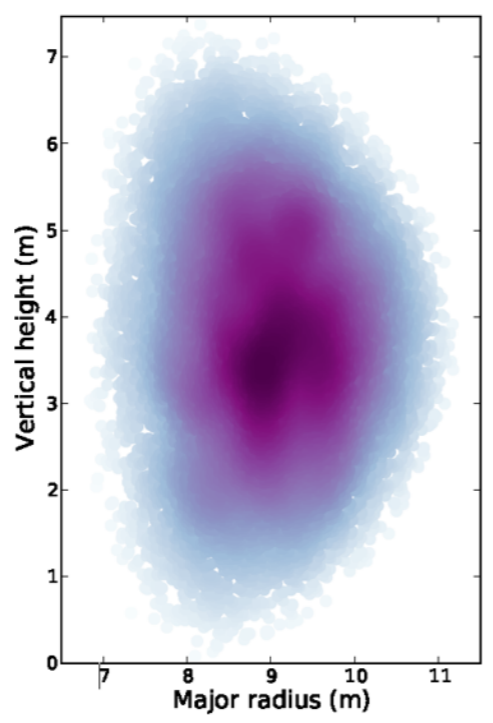
The spatial distribution of MCF plasma covers a larger area compared to ICF'
.
The energy distribution of MCF has less neutron scattering compared to ICF. Neutrons are:
- up scattered through collisions with alpha particles
- down scattered through collisions with DT nuclides
- plot shows initial neutron energy from a 50:50 DT plasma
<iframe src="https://prezi.com/embed/rnzt6pjj-xfu/?bgcolor=ffffff&lock_to_path=0&autoplay=1&autohide_ctrls=1&landing_data=bHVZZmNaNDBIWnNjdEVENDRhZDFNZGNIUE43MHdLNWpsdFJLb2ZHanI0eWk1QlBaUER3dVArS1hRQTAxNXdDZWNRPT0&landing_sign=ABm-Z3JCWCuKHnLF1Q-0yjuTsqyWAQdv3CEpUjcYcXk" title="W3Schools Free Online Web Tutorials" width="100%" height="100%"></iframe>
- (n,n)
- Neutron collides with the nucleus
- Neutron scatters of the nucleus losing energy
- Energy gained by the nucleus which recoils
- (n,n'g)
- Neutron capture by the nucleus
- Instantaneously re-emitted with less energy
- Nucleus in excited state
- Relaxes to ground state by emitting gamma rays
- At low energies the angular distribution is often isotropic
- As the neutron energy increases the scattering typically becomes more forward peaked
- Resonances in the cross section can impact the angular distribution probabilities
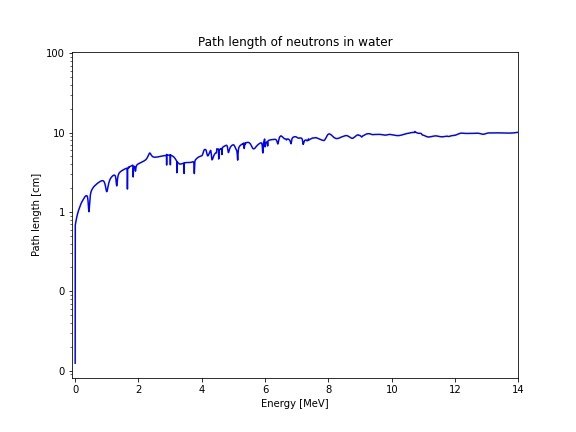
- Path length = 1 /
$\Sigma_{T}$ - A 14MeV neutron will lose energy via scattering interactions
- As the neutron energy decreases the path length also decreases
- Path length at thermal energy is more constant
The average logarithmic energy decrement (or loss) per collision (
| Hydrogen | Deuterium | Beryllium | Carbon | Uranium | |
|---|---|---|---|---|---|
| Mass of nucleus | 1 | 2 | 9 | 12 | 238 |
| Energy decrement | 1 | 0.7261 | 0.2078 | 0.1589 | 0.0084 |
The average number of collisions required to reduce the energy of the neutron from
If
| Hydrogen | Deuterium | Beryllium | Carbon | Uranium | |
|---|---|---|---|---|---|
| Number of collisions to thermalize | 20 | 25 | 85 | 115 | 2172 |
We should account for the likelihood of scattering.
The number density of the nucleus (ND) and the microscopic cross section (σ) combine to produce the macroscopic scattering cross section (Σ)
| Hydrogen | Deuterium | Beryllium | Carbon | Polyethylene | |
|---|---|---|---|---|---|
| Moderating power | 1.28 | 0.18 | 0.16 | 0.064 | 3.26 |
-
A grid of voxels / mesh elements can be overlaid on a geometry and the neutron response can be tallied in each voxel.
-
The mesh is typically 3D and defined with a top right and lower left coordinate.
- For our example we have a grid of voxels with only 1 voxel in one direction.
- This allows a pixel image of the tally result to be easily plotted.
- The geometry makes use of a two spheres and a plane surface type.
- The materials in each region respond very differently to neutrons
- The task has mesh tallies with different scores and plotting to visualize the result
- Fission of large atoms (e.g. U235)
- Results in two fission products far from stability
- New isotopes created during irradiation
- Radioactive isotopes decay and will eventually reach a point where decay rate is equal to activation rate.
- Decay is more noticeable once the plasma is shutdown.
- The activity is related to the irradiation time and the nuclide half life.
Replace the "your code here" sections to make the best reactor.
Chose the best options from a selection of materials.
Refine the design to:
- maximize Tritium Breeding Ratio (TBR)
- maximize blanket heating
- minimize damage to the conductor