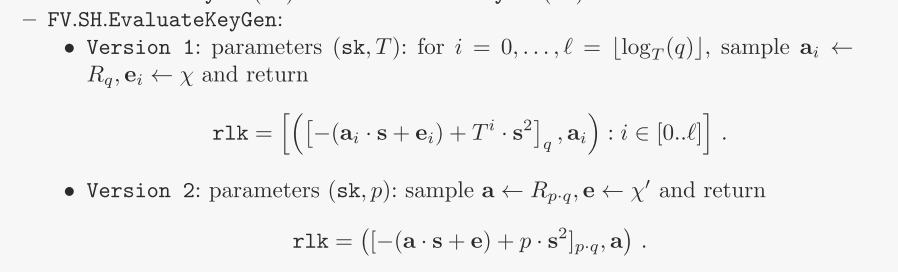Skip to content

CcoWzh/BFV

BranchesTags

Folders and files

NameName
Last commit message
Last commit date

Latest commit

 

History

2 Commits
3rdparty
3rdparty
 
 
src
src
 
 
.gitmodules
.gitmodules
 
 
CMakeLists.txt
CMakeLists.txt
 
 
README.md
README.md
 
 

Repository files navigation

本代码实现参考的是：

环境设置

实现BFV算法，先要用到FLINT这个快速数论库中的函数。 编译FLINT库，前提需要GMP、MPFR：

apt install libgmp-dev libmpfr-dev make autoconf libtool-bin

注意，这有个坑，安装的libgmp-dev、libmpfr-dev，版本号一般不是最新的，在编译时有问题

之后，执行：

git clone https://github.com/flintlib/flint.git && cd flint
./bootstrap.sh
./configure                        # ./configure --help for more options
make                               # make -j N，加速编译
make check                         # optional
make install                       # optional
make examples                      # optional
cd doc && make html && cd ..       # optional: documentation

这里要注意，在执行./configure命令时，是会检察GMP、MPFR版本的，需要满足：

建议手动安装，安装参考：

运行

编译flint库：

cd ./3rdparty/flint
参考上述步骤编译

运行：

mkdir build
cd build
cmake ..
make
./bfv_test

运行示例： image.png

算法实现

image.png

参数设置

参数设置如下：

double PI = 3.1415926;
int bit_num;
int sigma;       // 离散高斯分布标准差
int B;           //[-B, B] 近似离散高斯分布
int d;           // 同态加密f=x^d + 1
int lamda;       // 系统安全参数
int Max = 10000; // 以概率ro 输出x的方法：随机生成 【0， 10000】 之间的数z，如果z小于（小于等于）ro*10000则输出x，否则不输出
int delta;       // 系统安全参数

int l;
fmpz_t q;        // 大质数。n一般是2的次幂，q比t大很多，因此密文空间比明文空间大得多
fmpz_t neg_Delta;
fmpz_t t;        // 明文空间，P=Rt=Zt[x]/(xn+1)
fmpz_t Delta_2;
fmpz_t Delta;    // 缩放系数Δ=⌊q/t⌋
fmpz_t T;

// 可达到128bit安全
void System_Param()
{

   sigma = 8;
   B = 10 * sigma;
   d = 8192;           // 2^13 = 8192
   bit_num = 128;
   char *str1 = "100000000000000000000000000000000";
   char *str2 = "8000";
   // 密文空间
   fmpz_set_str(q, str1, 16);   // q = 34028236692093846346337460743176821145665536 = pow(2, 128)
   // 明文空间
   fmpz_set_str(t, str2, 16);   // t = pow(2, 15)=32768
   fmpz_cdiv_q(Delta, q, t);    // 缩放系数Δ=⌊q/t⌋
   fmpz_neg(neg_Delta, Delta);  // neg_Delta = -1*Delta
   fmpz_cdiv_q_ui(Delta_2, Delta, 2); // Delta_2 = Delta/2的商
   // q平方根的整数部分
   fmpz_sqrt(T, q);             // pow(2, 64) = 18446744073709551616
   l = fmpz_flog(q, T);         // log_T(q),向下取整

}

BFV用到的随机分布

BFV用到的随机分布主要有：

  • $R_2$：密钥的采样分布，对整数系数为{-1,0,1}的多项式进行采样（系数是对模3环上的均匀采样：$Z_3$）。
  • $\chi$：随机错误分布，定义为R上参数为μ和σ的离散高斯分布，以某个整数β为界。 根据当前版本的同态加密标准, $(\mu,\sigma,\beta)$被设定为$(0,\frac{8}{\sqrt{2\pi}} \approx 3.2,\lfloor 6\sigma\rceil =19)$。
  • $R_q$：$R_q$上的均匀随机分布。

我们注意到，参数$(t,q,n)$的选择是针对具体应用的，也是由所需的安全级别驱动的。关于一组可接受的参数，参考同态加密标准ACC+18中的表1和表2。作为一个经验法则，只要感兴趣的目标应用仍然可以在FHE中实现，就应该选择最小化这些参数。

高斯分布

// D_{Z, \sigma}
long SampleZ(int seed)
{
   long xx;
   long z;
   double ro;
   long zz;
   int b;
   srand(time(NULL) + seed);
   do
   {
      xx = rand() % B;
      z = rand() % Max;
      ro = exp(-(PI * xx * xx) / (sigma * sigma));
   } while (!(z < ro * Max));
   b = rand() % 2;
   if (b == 0)
      b = -1;
   xx = xx * b;
   return xx;
}

// 生成（近似）离散高斯分布
void SampleD(fmpz_poly_t v, int seed)
{
   int i;
   long x;
   for (i = d - 1; i >= 0; i--)
   {
      x = SampleZ(i + seed);
      fmpz_poly_set_coeff_si(v, i, x);
   }
}

密钥的采样分布

void Gen_R2(fmpz_poly_t v, int seed)
{
   int i;      
   srand(time(NULL)+seed);
   int b;
   //d是f(x)=2^d+1的多项式最高次数，d=8192
   for(i = d-1; i >= 0; i--)
   {
      b = rand()%2;
      // 设置多项式v的第i个系数为b
      fmpz_poly_set_coeff_ui(v, i, b);
   }
}

这其实就生成了一个向量，这个向量的元素全是mod2的元素（即，0、1），向量元素的数量为d个：

8192  0 0 1 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 1 1 0 1 1 0 0 1 1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 1 0 1 1 0 1 0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 1 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 0 0 0 1 1 0 1 0 0 0 0 0 1 1 0 1 0 0 0 0 .....（未复制完整）

环q上的均匀随机分布

//这个的问题是好像没有小一点的数。。计算上应该效率要差一些，但是这个正常的吗？不是很清楚
void Gen_Rq(fmpz_poly_t v)
{
    int i;
    fmpz_t t;
    fmpz_init(t);
    for(i = d-1; i >= 0; i--)
       {
          Gen_Rq_div_2(t, i);
          fmpz_poly_set_coeff_fmpz(v, i, t);

       }

    fmpz_clear(t);
}

生成公私钥

私钥SK是 random ternary polynomial ，也就是系数取自$R_2=-1,0,1$的多项式 公钥PK是$R_q$上的多项式，由一对多项式构成：$(pk_1,pk_2)$，定义如下: $pk_1 = [-1(ask+e)]_q \pk_2=a$ 其中$a$是采样自$R_q$上的随机多项式，$e$是采样自$\chi$的随机多项式。符号$[]_q$表示多项式的系数运算以$q$为模数进行。总之，$a$定义$R_q$上，所有运算都定义在$Z_q$上面模$x^{n}+1$的多项式环。

生成私钥

$s \in R_2$

void secret_key_Gen(fmpz_poly_t sk)
{
  // 是环R2上的随机采样
   Gen_R2(sk, 1);
}

示例：

8192  0 0 1 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 1 1 0 1 1 0 0 1 1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 1 0 1 1 0 1 0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 0 1 0 1 1 0 0 1 1 0 1 1 0 1 1 1 1 0 1 1 1 1 1 1 0 1 1 1 0 0 0 1 1 0 1 0 0 0 0 0 1 1 0 1 0 0 0 0 .....（未复制完整）

生成公钥

$pk = ([-1(a*s+e)]q ,a) \ a \in R_q \ s \in R_2, \ e \in D{Z, sigma}^d$

void public_key_Gen(fmpz_poly_t sk, fmpz_poly_t pk_p0, fmpz_poly_t pk_p1)
{  
    //pk = ( [-(as+e)]_q, a ), a \in R_q, s \in R_2,  e \in D_{Z, sigma}^d
    fmpz_poly_t e;    
    fmpz_poly_t temp;
    fmpz_poly_init(e);
    fmpz_poly_init(temp);

    SampleD(e, 1);
    Gen_Rq(pk_p1);
    // 组装pk_0
    fmpz_poly_mul(temp, pk_p1, sk);   
    fmpz_poly_add(temp, temp, e); 
    fmpz_poly_neg(temp, temp);
    fmpz_poly_scalar_smod_fmpz(temp, temp, q);
    fmpz_poly_set(pk_p0, temp);
    // 释放内存
    fmpz_poly_clear(e);
    fmpz_poly_clear(temp);

}

示例： $e$是采样自$\chi$的随机多项式，是一组相对来说很小的数，示例为：

8190  0 -2 -3 -3 -3 0 -3 4 -6 -3 -2 -3 2 0 -2 4 -1 0 -5 -4 8 4 3 -3 4 0 4 -4 -55 2 -1 -1 -2 2 -1 0 3 2 1 4 0 1 0 3 4 -3 -3 1 -1 -1 -2 4 0 -1 3 2 3 -1 6 3 3 5 0 3 0 0 3 -9 5 -6 0 2 -4 -6 -3 6 1 -7 1 8 1 -2 3 4 -3 -4 -9 7 -4 -3 2 0 3 0 -1 -3 -1 1 -8 0 2 0 1 0 -1 -1 3 0 -2 0 0 .....（未复制完整）

$pk_2$，即，$a$是采样自$R_q$上的随机多项式，示例为：

8192  331905331559733804788244285082160240614100570385 140726478588109206723772005670782302828333052780 116663651631441389138552166755723762482 557223223557859865266956471441997142347961049645 408941017818115482178463533869370999477989941820 692360840059540263887314725256864820967851430645 678825885773799997450126381292932404035605420125 16061572095990657007193197201424984870 150554311454088984370955373134374760244 411225095710460614734641857633717172445930322830 ......（未复制完整）

$pk_1$，示例为：

16381  122275889201066093381561088779706035951 -162855716776770439475870868991654966122 -116663651631441389138552166755723762479 136751941251596197146633621250051956182 -102915467278864585329392502653362910026 112068363621243104302107430545745422478 129638428626974672224960143523720730888 4026717524164151000888257292903208823 101288640238514997528099264114376461417 -55755616027844001104061583667385352653 -147562599255700303064831326736931931392 -45997335501148544878337680634815429276 123526117531181688713023245517536035053 -44168451372754308119595817539390145500 125391326064984976877394473246691694475 124034159554476870194663062681714806148 3867239891109191601365773419 161666692549471964981334013151454485893 107501733670582311828028052710938080802 -118326415704824479831479160758222979438 108514839532980705334575306007683531981 -8129619004875019130244412094779815932 ......（未复制完整）

这里需要弄清楚一个问题： 为什么pk_1的长度是16381？是因为 8192+8190-1 吗？这样是不是说明那个加号是拼接的意思？

明文编码

image.png 将明文表示为二进制：

void Encode(int m, fmpz_poly_t pm)
{ 
   int sgn;
   if(m < 0) sgn = -1;
   else sgn = 1;
   int num;
   m = abs(m);
   double bitnum = log2(m);
   int i; 
   int bit; 
   if(bitnum == (int)bitnum) num  = (int)bitnum + 1;
      else num = (int)bitnum + 1; 

   for(i = 0; i < num; i++) 
     {
        bit = m % 2;
        fmpz_poly_set_coeff_ui(pm, i, bit);
        m = m/2;
     }
   fmpz_poly_scalar_mul_si(pm, pm, sgn);
    
}

加密和解密

image.png

加密

void SH_Encrypt(fmpz_poly_t m, fmpz_poly_t pk_p0, fmpz_poly_t pk_p1, fmpz_poly_t c0, fmpz_poly_t c1)
{
   fmpz_poly_t u;
   fmpz_poly_t e1;
   fmpz_poly_t e2;
   fmpz_poly_t temp;
   fmpz_poly_t temp1;
   fmpz_poly_init(u);
   fmpz_poly_init(e1);
   fmpz_poly_init(e2);
   fmpz_poly_init(temp);
   fmpz_poly_init(temp1);
   // u是环R2上的采样
   Gen_R2(u, 2);
   // e1、e2是高斯分布采样
   SampleD(e1, 2);
   SampleD(e2, 3);

   fmpz_poly_mul(temp, pk_p0, u); 
   fmpz_poly_add(temp, temp, e1);
   fmpz_poly_scalar_mul_fmpz(temp1, m, Delta);  
   fmpz_poly_add(temp, temp, temp1);
   fmpz_poly_scalar_smod_fmpz(temp, temp, q);
   fmpz_poly_set(c0, temp);
   fmpz_poly_mul(temp, pk_p1, u);
   fmpz_poly_add(temp, temp, e2);
   fmpz_poly_scalar_smod_fmpz(c1, temp, q);
   
   fmpz_poly_clear(u);
   fmpz_poly_clear(e1);
   fmpz_poly_clear(e2);
   fmpz_poly_clear(temp);
   fmpz_poly_clear(temp1);

}

解密

void SH_Decrypt(fmpz_poly_t sk, fmpz_poly_t c0, fmpz_poly_t c1)
{
   fmpz_poly_t temp;
   fmpz_poly_init(temp);  
   fmpz_poly_mul(temp, c1, sk);
   fmpz_poly_add(temp, temp, c0);
   fmpz_poly_scalar_smod_fmpz(temp, temp, q);   
   fmpz_poly_nearest_fmpz(temp);
   fmpz_poly_scalar_smod_fmpz(temp, temp, t);

   printf("\ntemp*t/q is \n");
   fmpz_poly_print(temp);
 
   fmpz_poly_clear(temp);

}

同态计算

同态加法

//c0 = (c_00, c_01), c1 = (c_10, c_11), c = c0+c1
void SH_Add(fmpz_poly_t c_00, fmpz_poly_t c_01, fmpz_poly_t c_10, fmpz_poly_t c_11, fmpz_poly_t c0, fmpz_poly_t c1)
{
    fmpz_poly_t temp;
    fmpz_poly_init(temp);
    fmpz_poly_add(temp, c_00, c_10);
    fmpz_poly_scalar_smod_fmpz(c0, temp, q);   
    
    fmpz_poly_add(temp, c_01, c_11);
    fmpz_poly_scalar_smod_fmpz(c1, temp, q);
    fmpz_poly_clear(temp);

}

同态乘法

同态乘法的算法如下： image.png

同态乘法进行多次后会使得计算复杂度、密文冗余快速增大，也就是有限次数的同态加密。为了做到全同态加密，BFV方案给出了一个安全并且有效的解决方案：利用额外的评估密钥rlk进行Relinearization，既可以降维度，又可以减少误差的累积，从而达到全同态加密的效果。

发现有一个共同的计算：$[\lfloor\frac{t(*)}{q}\rceil]_q$，因此，将这个计算剥离出来：

void fmpz_poly_nearest_fmpz(fmpz_poly_t v)
{
   long deg = fmpz_poly_degree(v);  // 多项式v的度，即，最高次项的次数
   int i;   
   fmpz_t temp;
   fmpz_t temp1;
   fmpz_init(temp);
   fmpz_init(temp1);

   for(i = 0; i <= deg; i++)
      {
         //设置temp等于v的第i个系数
         fmpz_poly_get_coeff_fmpz(temp, v, i);
         // 绝对值
         fmpz_abs(temp1, temp);
         // temp1=temp1/Delta,四舍五入方法为fdiv
         fmpz_fdiv_r(temp1, temp1, Delta);

         if(fmpz_equal(temp, Delta) == 1) {fmpz_set_ui(temp, 1);}
         else if(fmpz_equal(temp, neg_Delta) == 1) {fmpz_set_si(temp, -1);}
         else if(fmpz_is_zero(temp) == 1) {fmpz_set_ui(temp, 0);}
         // 对元素取模q，即，mod q
         else if(fmpz_sgn(temp) == -1 && fmpz_cmp(temp1, Delta_2) > 0)  {fmpz_fdiv_q(temp, temp, Delta);}
         else if(fmpz_sgn(temp) == -1 && fmpz_cmp(temp1, Delta_2) <= 0)  {fmpz_cdiv_q(temp, temp, Delta);}
         else if(fmpz_sgn(temp) == 1 && fmpz_cmp(temp1, Delta_2) >= 0)  {fmpz_cdiv_q(temp, temp, Delta);}
         else{fmpz_fdiv_q(temp, temp, Delta);}

         fmpz_poly_set_coeff_fmpz(v, i, temp);           
      }

   fmpz_clear(temp);
   fmpz_clear(temp1); 
}

之后，两数相乘，会从二维变成三维：

void SH_Mul(fmpz_poly_t c_00, fmpz_poly_t c_01, fmpz_poly_t c_10, fmpz_poly_t c_11, fmpz_poly_t c0, fmpz_poly_t c1, fmpz_poly_t c2)
{
   fmpz_poly_t temp1;
   fmpz_poly_t temp2;

   fmpz_poly_init(temp1);
   fmpz_poly_init(temp2);

   fmpz_poly_mul(c0, c_00, c_10);   
   fmpz_poly_nearest_fmpz(c0);

   fmpz_poly_mul(temp1, c_00, c_11);
   fmpz_poly_mul(temp2, c_01, c_10);
   fmpz_poly_add(c1, temp1, temp2);
   fmpz_poly_nearest_fmpz(c1);

   fmpz_poly_mul(c2, c_01, c_11);
   fmpz_poly_nearest_fmpz(c2);

   fmpz_poly_clear(temp1);
   fmpz_poly_clear(temp2);
   
}

对乘法后的结果进行解密，获得解密后的数据：

void SH_DecMul(fmpz_poly_t sk, fmpz_poly_t c0, fmpz_poly_t c1, fmpz_poly_t c2)
{
  fmpz_poly_t temp;
  fmpz_poly_t temp2;
  fmpz_poly_init(temp);
  fmpz_poly_init(temp2);

  fmpz_poly_mul(temp, c1, sk);

  fmpz_poly_mul(temp2, c2, sk);
  fmpz_poly_mul(temp2, temp2, sk);

  fmpz_poly_add(temp,c0, temp);
  fmpz_poly_add(temp, temp, temp2);

  fmpz_poly_scalar_smod_fmpz(temp, temp, q);   

  fmpz_poly_nearest_fmpz(temp);

  fmpz_poly_scalar_smod_fmpz(temp, temp, t);
   
  fmpz_poly_clear(temp);
  fmpz_poly_clear(temp2);
}

重线性化

image.png 首先，生成重线性化密钥：

void ReKey_Gen(fmpz_poly_t sk, fmpz_poly_t* rlk_r0, fmpz_poly_t* rlk_r1)
{
   fmpz_poly_t e;
   int i;
   fmpz_poly_t temp1;
   fmpz_t temp2;
   fmpz_poly_t temp3;
   fmpz_poly_init(e);
   fmpz_poly_init(temp1);
   fmpz_init(temp2);
   fmpz_poly_init(temp3);
   
  
   for(i = 0; i < l; i++)
      {
         Gen_Rq(rlk_r1[i]);
         SampleD(e, i+9);
         fmpz_poly_mul(temp1, rlk_r1[i], sk);
         fmpz_poly_add(temp1, temp1, e);
         fmpz_poly_neg(temp1, temp1);
         fmpz_pow_ui(temp2, T, i);
         fmpz_poly_mul(temp3, sk, sk);     
         fmpz_poly_scalar_mul_fmpz(temp3, temp3, temp2);
         fmpz_poly_add(temp1, temp1, temp3);
         fmpz_poly_scalar_smod_fmpz(rlk_r0[i], temp1, q);  
         
      }
   
   fmpz_poly_clear(temp1);
   fmpz_clear(temp2);
   fmpz_poly_clear(temp3);
   fmpz_poly_clear(e);

}

随后，对乘法后的“三维”数据进行重线性化，变成“两维” image.png

void  Relinear(fmpz_poly_t* rlk_r0, fmpz_poly_t* rlk_r1, fmpz_poly_t c0, fmpz_poly_t c1, fmpz_poly_t c2, fmpz_poly_t _c0, fmpz_poly_t _c1)
{
   int i; 
   int deg = fmpz_poly_degree(c2);

   fmpz_poly_t *c2_i;
   c2_i = (fmpz_poly_t *)malloc(sizeof(fmpz_poly_t)*l);

   fmpz_t temp;  
   fmpz_t temp1;
   fmpz_poly_t temp2;
   fmpz_poly_t temp3;
 
   for(i = 0; i < l; i++)
      fmpz_poly_init(c2_i[i]);

   fmpz_init(temp);
   fmpz_init(temp1);
   fmpz_poly_init(temp2);
   fmpz_poly_init(temp3);

   for(i = 0; i <= deg; i++)
      {
         fmpz_poly_get_coeff_fmpz(temp, c2, i);
         
         fmpz_abs(temp1, temp);
         if(fmpz_cmp(temp1, T) < 0)
            fmpz_poly_set_coeff_fmpz(c2_i[0], i, temp); 
         else 
            {
               fmpz_fdiv_qr(temp, temp1, temp, T);
               fmpz_poly_set_coeff_fmpz(c2_i[0], i, temp1);
               fmpz_poly_set_coeff_fmpz(c2_i[1], i, temp);
            }

      }

   fmpz_poly_mul(temp2, rlk_r0[0], c2_i[0]);
   fmpz_poly_mul(temp3, rlk_r0[1], c2_i[1]);
  
   fmpz_poly_add(temp2, temp2, temp3);
   fmpz_poly_add(temp2, temp2, c0);
   fmpz_poly_scalar_smod_fmpz(_c0, temp2, q); 

   fmpz_poly_mul(temp2, rlk_r1[0], c2_i[0]);
   fmpz_poly_mul(temp3, rlk_r1[1], c2_i[1]);
  
   fmpz_poly_add(temp2, temp2, temp3);
   fmpz_poly_add(temp2, temp2, c1);
   fmpz_poly_scalar_smod_fmpz(_c1, temp2, q); 

   for(i = 0; i < l; i++)
      fmpz_poly_clear(c2_i[i]);
 
   fmpz_clear(temp);
   fmpz_clear(temp1);
   fmpz_poly_clear(temp2);
   fmpz_poly_clear(temp3);

}

About

使用C/C++实现bfv同态算法

Resources

Readme
Activity

Stars

0 stars

Watchers

1 watching

Forks

0 forks
Report repository

Releases

No releases published

Packages

No packages published

Languages