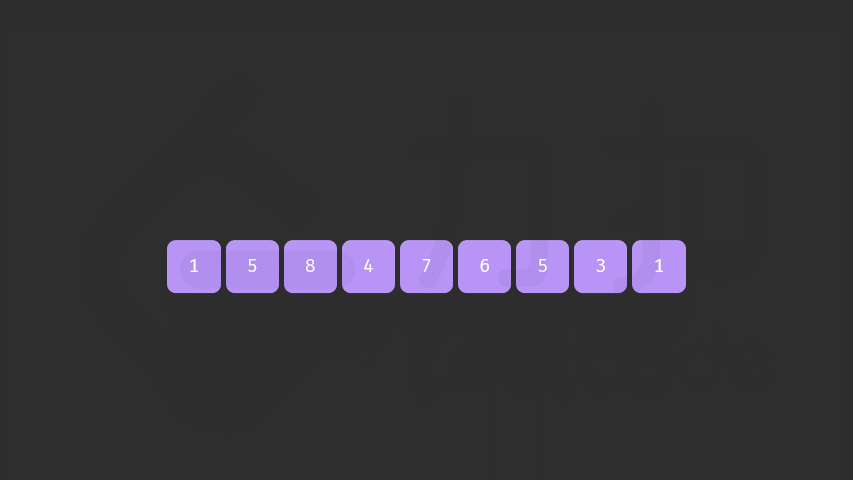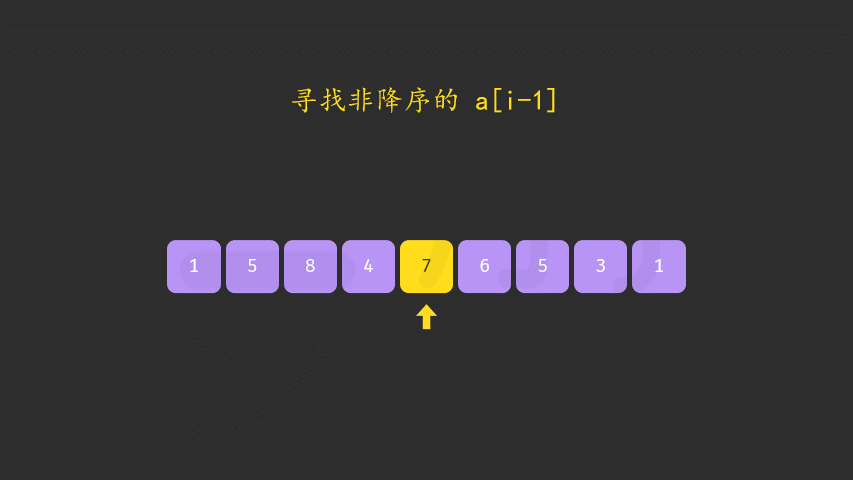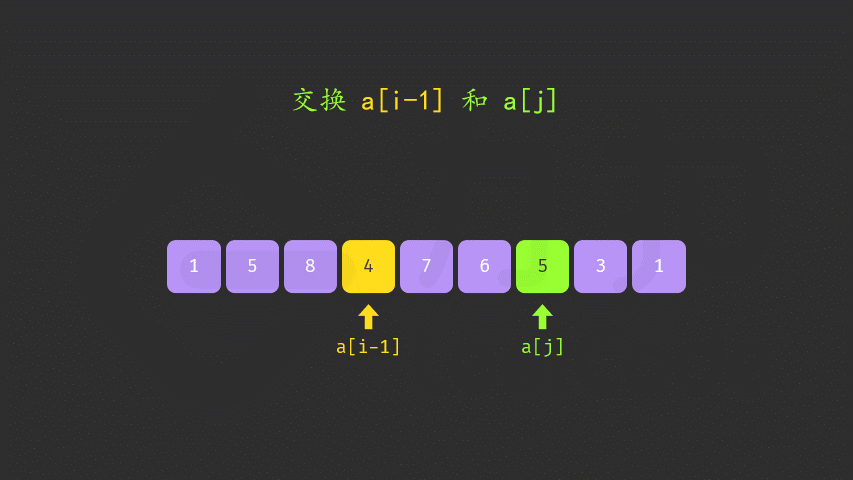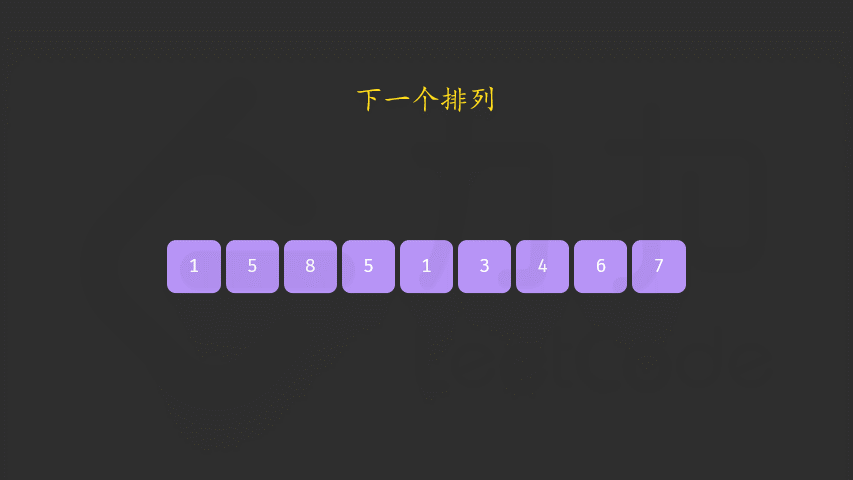这个仓库用来记录自己的力扣刷题以及进行总结,总结类似的题型,避免无效刷题
“在一维数组中找第一个满足某种条件的数”的场景就是典型的单调栈应用场景
从名字也可以看出, 它最大的特点就是单调, 也就是栈中的元素要么递增, 要么递减, 如果有新的元素不满足这个特点, 就不断的将栈顶元素出栈, 直到满足为止, 这就是它最重要的思想.
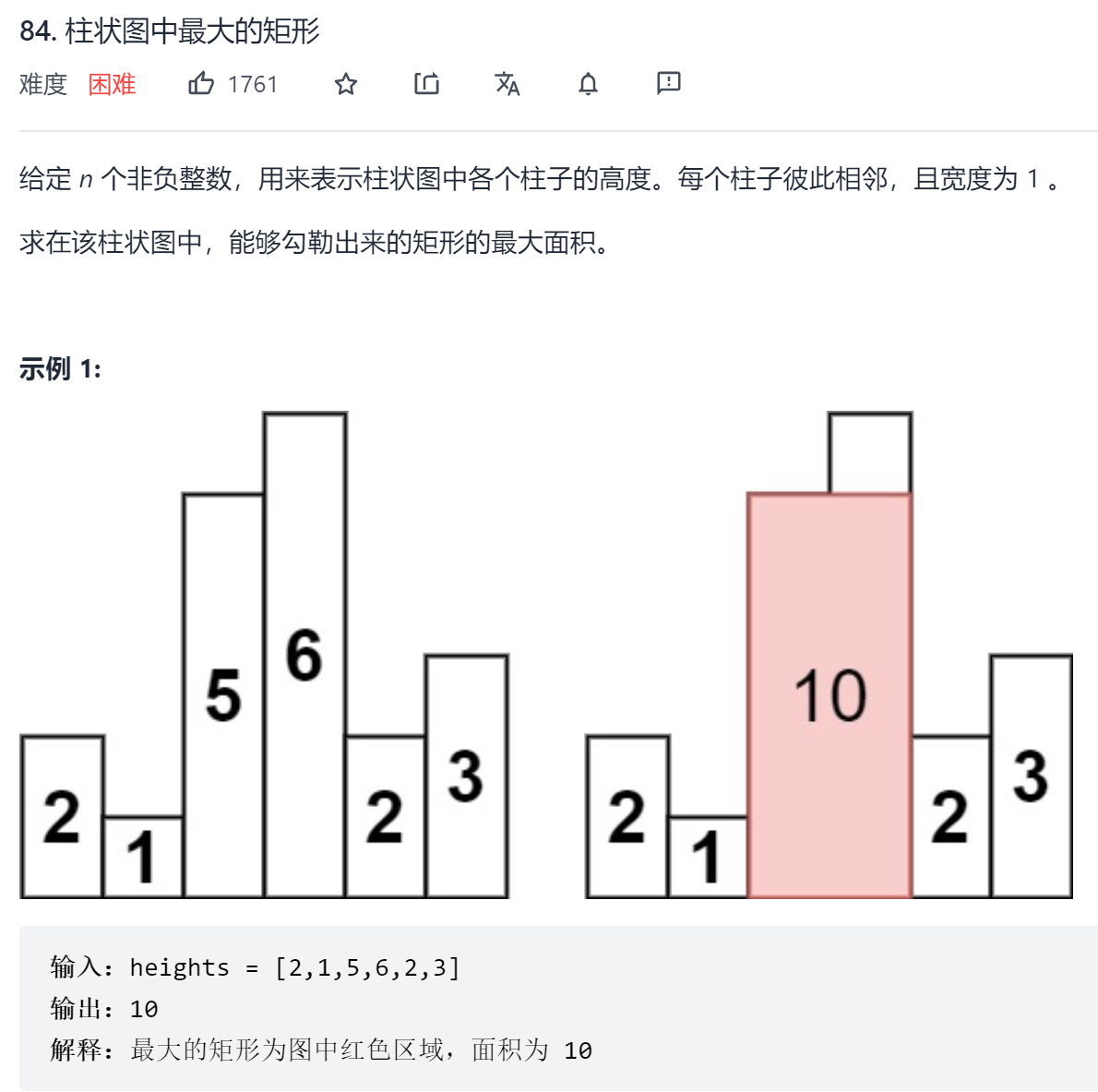
这一题考察的就是单调栈的运用,求柱状图中的最大矩形,要考虑的是如何找到一根柱子的左右两边第一个小于自己高度的柱子,然后即可得到面积
class Solution {
public:
int largestRectangleArea(vector<int>& heights) {
// 重要,要在最右边加个高度为0的柱子
heights.push_back(0);
int n = heights.size();
// s相当于存左边界
stack<int> s;
int res = INT_MIN;
for (int i = 0; i < n; i++) {
// 右边沿:正好是i(由于单调栈的性质,第i个柱子就是右边第一个矮于A的柱子)
// 左边沿:单调栈中紧邻A的柱子。(如果A已经出栈,那么左边沿就是A出栈后的栈顶)
// 当A出栈后,单调栈为空时,那就是说明,A的左边没有比它矮的。左边沿就可以到0.
while (!s.empty() && heights[i] <= heights[s.top()]) {
int h = heights[s.top()];
s.pop();
int left = s.empty()? -1: s.top();
res = max(res, h * (i - left - 1));
}
s.push(i);
}
return res;
}
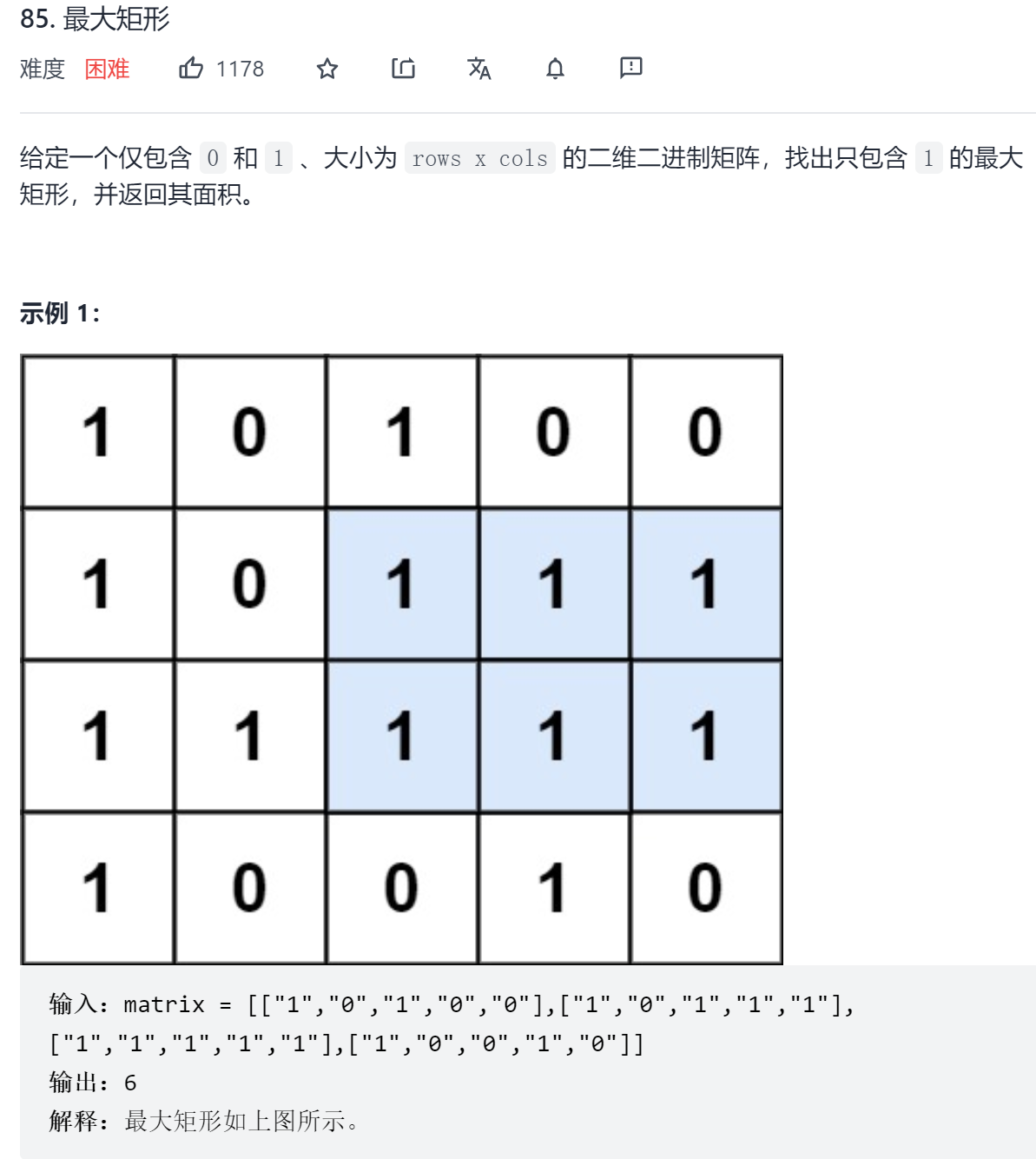
};同样,这一题可以看做是多个柱状图中找最大面积,做法与上一题基本一致,区别在于要逐步从第一行到最后一行将矩阵看做柱状图,再重复调用上一题的解题方法即可
class Solution {
private:
int res;
public:
int maximalRectangle(vector<vector<char>>& matrix) {
int n = matrix.size();
int m = matrix[0].size();
for (int i = 0; i < n; i++) {
vector<int> tmp(m);
for (int k = 0; k < m; k++) {
int j = i;
while (j < n && matrix[j][k] == '1') {
j++;
}
tmp[k] = j - i;
}
solve(tmp);
}
return res;
}
void solve(vector<int> heights) {
heights.push_back(0);
int n = heights.size();
stack<int> s;
for (int i = 0; i < n; i++) {
while (!s.empty() && heights[i] < heights[s.top()]) {
int h = heights[s.top()];
s.pop();
int left = s.empty()? -1: s.top();
res = max(res, h * (i - left - 1));
}
s.push(i);
}
}
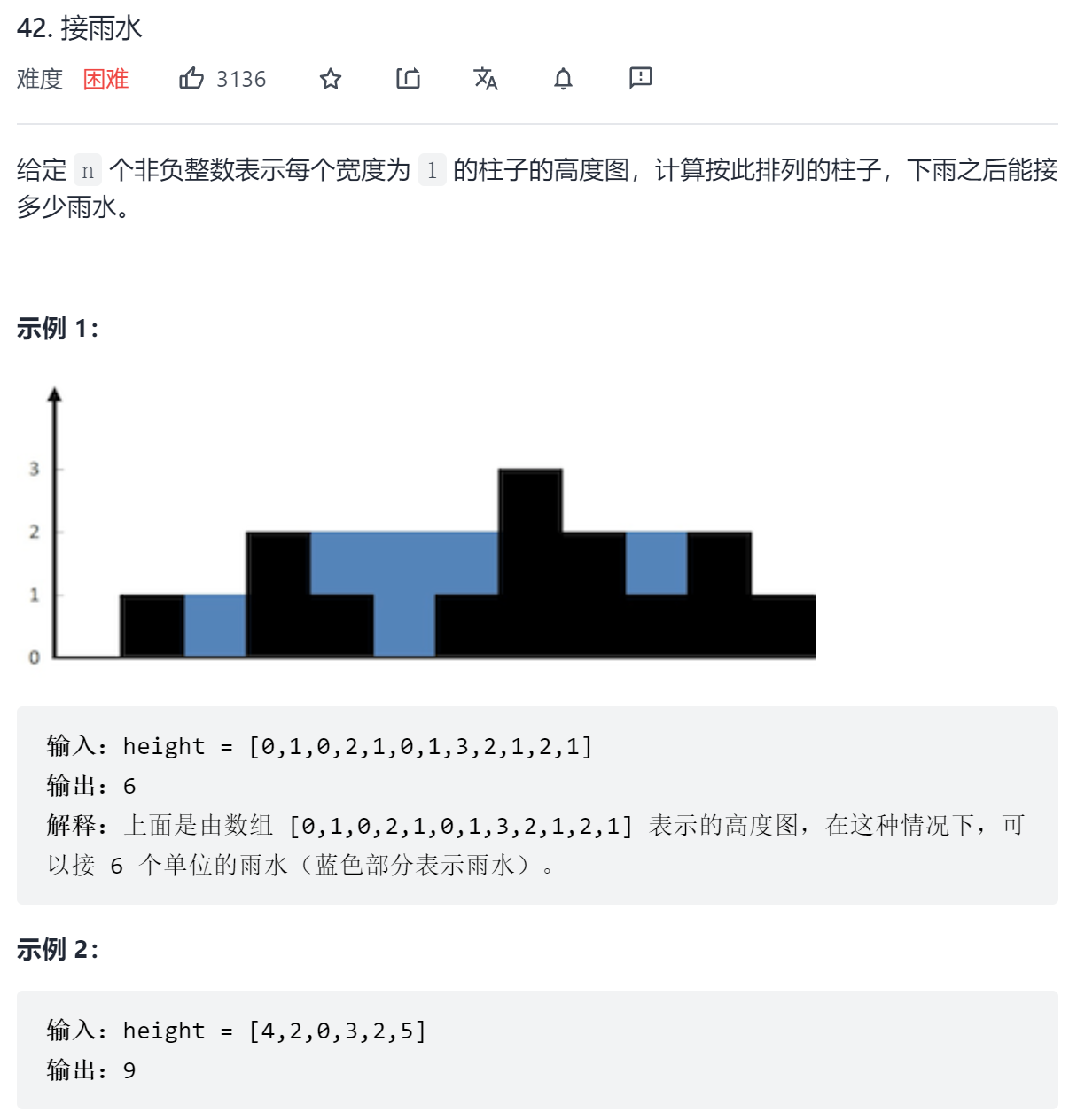
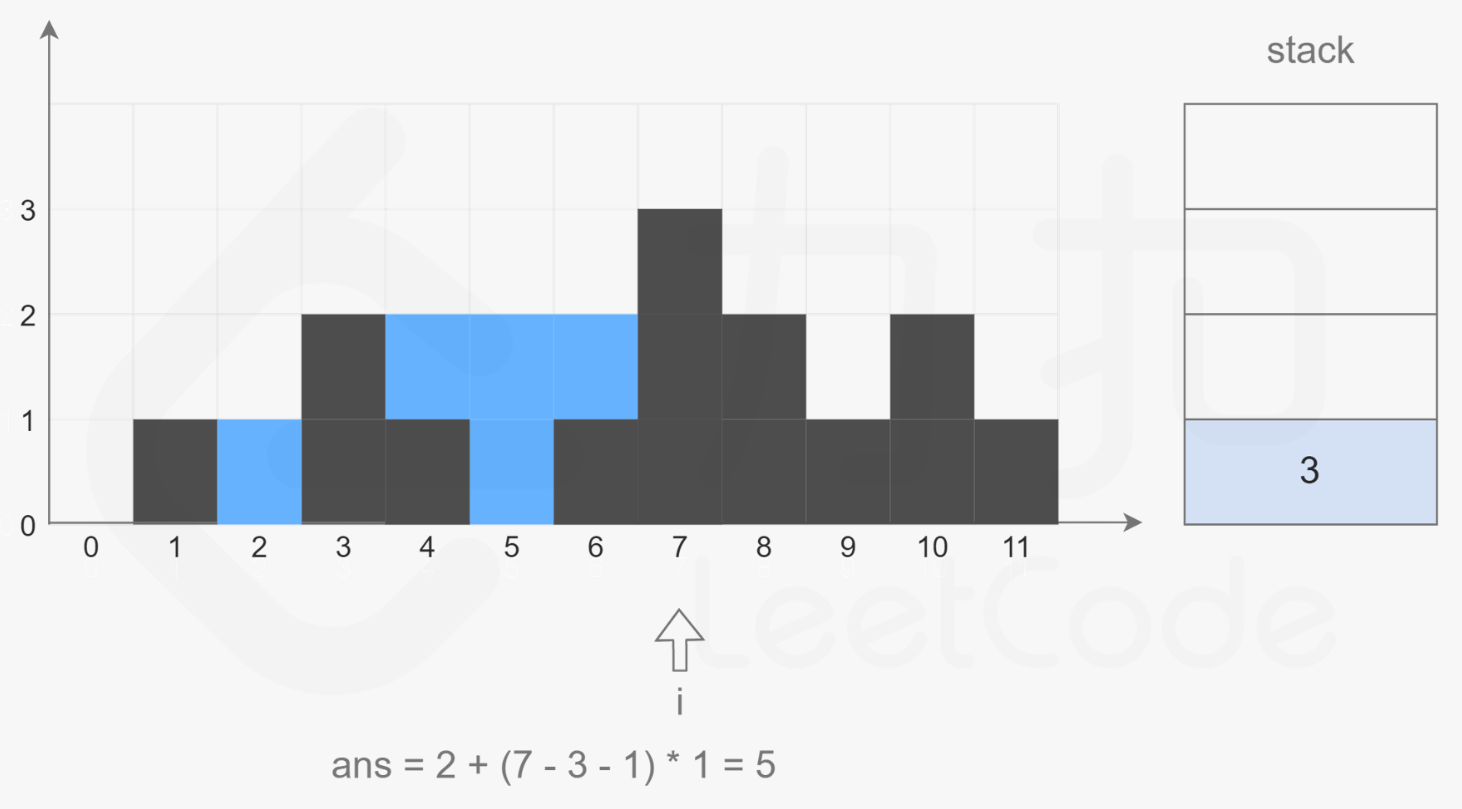
};对于下标 i,下雨后水能到达的最大高度等于下标 i 两边的最大高度的最小值,下标 i 处能接的雨水量等于下标 i 处的水能到达的最大高度减去 height[i]。
朴素的做法是对于数组 height 中的每个元素,分别向左和向右扫描并记录左边和右边的最大高度,然后计算每个下标位置能接的雨水量。假设数组 height 的长度为 n,该做法需要对每个下标位置使用 O(n) 的时间向两边扫描并得到最大高度,因此总时间复杂度是 O(n^2),但是向左和向右扫描并记录左边和右边的最大高度这一点很明显满足单调栈的特性,因此我们可以用单调栈来做。
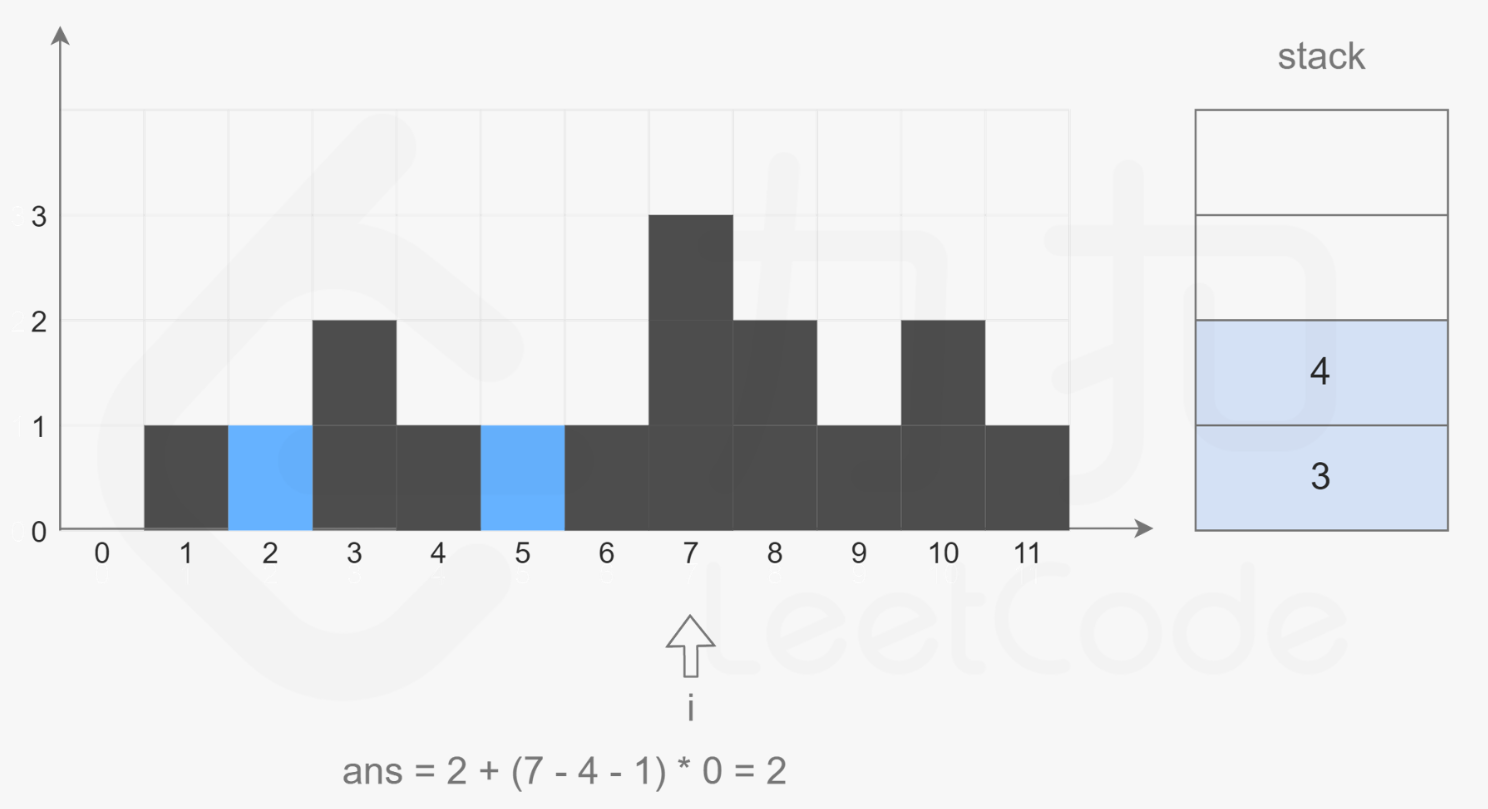
维护一个单调栈,单调栈存储的是下标,满足从栈底到栈顶的下标对应的数组 height 中的元素递减。遍历柱子,当不满足当前遍历到的柱子小于栈顶柱子的高度时,说明栈顶右边第一个大于他的柱子出现了,然后栈顶出栈,此时的栈顶就是左边第一个大于出栈柱子的柱子,因此可以计算出栈柱子的接水面积了。
class Solution {
public:
int trap(vector<int>& height) {
int ans = 0;
stack<int> stk;
int n = height.size();
for (int i = 0; i < n; ++i) {
while (!stk.empty() && height[i] > height[stk.top()]) {
int top = stk.top();
stk.pop();
if (stk.empty()) {
break;
}
int left = stk.top();
int currWidth = i - left - 1;
int currHeight = min(height[left], height[i]) - height[top];
ans += currWidth * currHeight;
}
stk.push(i);
}
return ans;
}
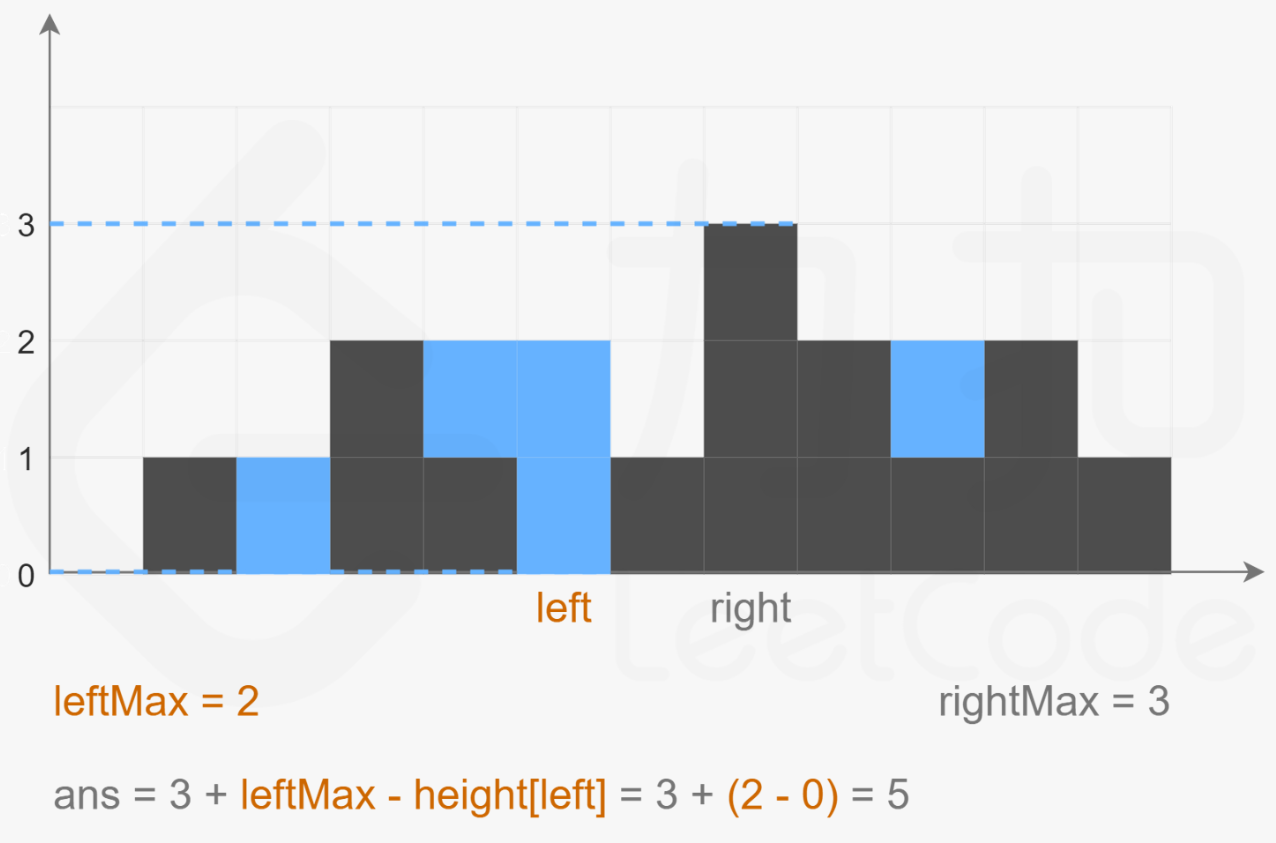
};此题还可以采用双指针来做,维护两个指针 left 和 right,以及两个变量 leftMax 和 rightMax,初始时 left=0,right=n-1,leftMax=0,rightMax=0。指针 left 只会向右移动,指针 right 只会向左移动,在移动指针的过程中维护两个变量 leftMax 和 rightMax 的值。
class Solution {
public:
int trap(vector<int>& height) {
int ans = 0;
int left = 0, right = height.size() - 1;
int leftMax = 0, rightMax = 0;
while (left < right) {
leftMax = max(leftMax, height[left]);
rightMax = max(rightMax, height[right]);
if (height[left] < height[right]) {
ans += leftMax - height[left];
++left;
} else {
ans += rightMax - height[right];
--right;
}
}
return ans;
}
};滑动窗口模式是用于在给定数组或链表的特定窗口大小上执行所需的操作,比如寻找包含所有 1 的最长子数组。从第一个元素开始滑动窗口并逐个元素地向右滑,并根据你所求解的问题调整窗口的长度。在某些情况下窗口大小会保持恒定,在其它情况下窗口大小会增大或减小。
下面是一些你可以用来确定给定问题可能需要滑动窗口的方法:
- 问题的输入是一种线性数据结构,比如链表、数组或字符串
- 你被要求查找最长/最短的子字符串、子数组或所需的值
你可以使用滑动窗口模式处理的常见问题:
- 大小为 K 的子数组的最大和(简单)
- 带有 K 个不同字符的最长子字符串(中等) ----采用滑动窗口,用HashMap记录窗口中间的字符串是否满足要求
- 寻找字符相同但排序不一样的字符串(困难)
这题与带有 K 个不同字符的最长子字符串类似,采用滑动窗口与hashset记录双指针中间的字符串是否有相同的字符,在每一步的操作中,我们会将左指针向右移动一格,表示我们开始枚举下一个字符作为起始位置,然后我们可以不断地向右移动右指针,但需要保证这两个指针对应的子串中没有重复的字符。在移动结束后,这个子串就对应着 以左指针开始的,不包含重复字符的最长子串。我们记录下这个子串的长度,最后找到最大值即可。
class Solution {
public:
int lengthOfLongestSubstring(string s) {
// 哈希集合,记录每个字符是否出现过
unordered_set<char> occ;
int n = s.size();
// 右指针,初始值为 -1,相当于我们在字符串的左边界的左侧,还没有开始移动
int rk = -1, ans = 0;
// 枚举左指针的位置,初始值隐性地表示为 -1
for (int i = 0; i < n; ++i) {
if (i != 0) {
// 左指针向右移动一格,移除一个字符
occ.erase(s[i - 1]);
}
while (rk + 1 < n && !occ.count(s[rk + 1])) {
// 不断地移动右指针
occ.insert(s[rk + 1]);
++rk;
}
// 第 i 到 rk 个字符是一个极长的无重复字符子串
ans = max(ans, rk - i + 1);
}
return ans;
}
};class Solution {
public:
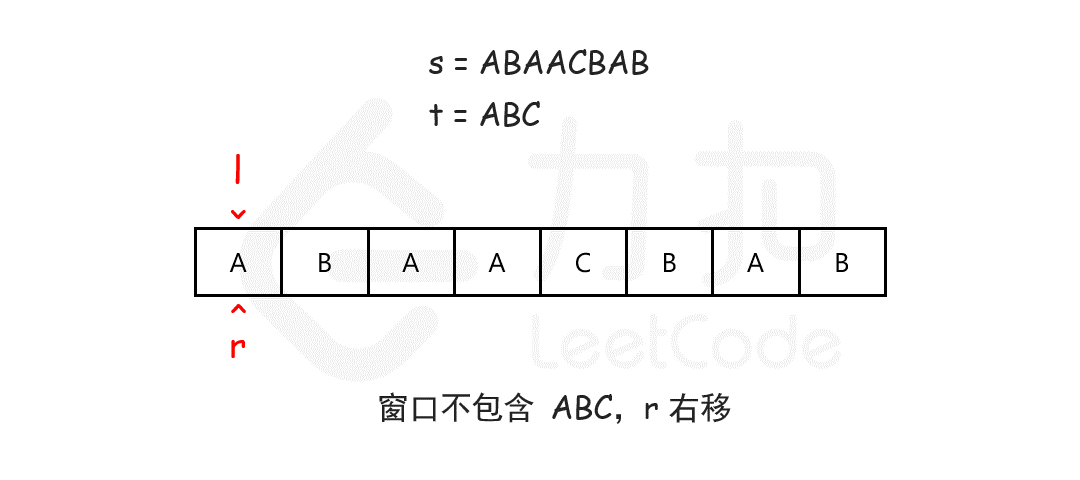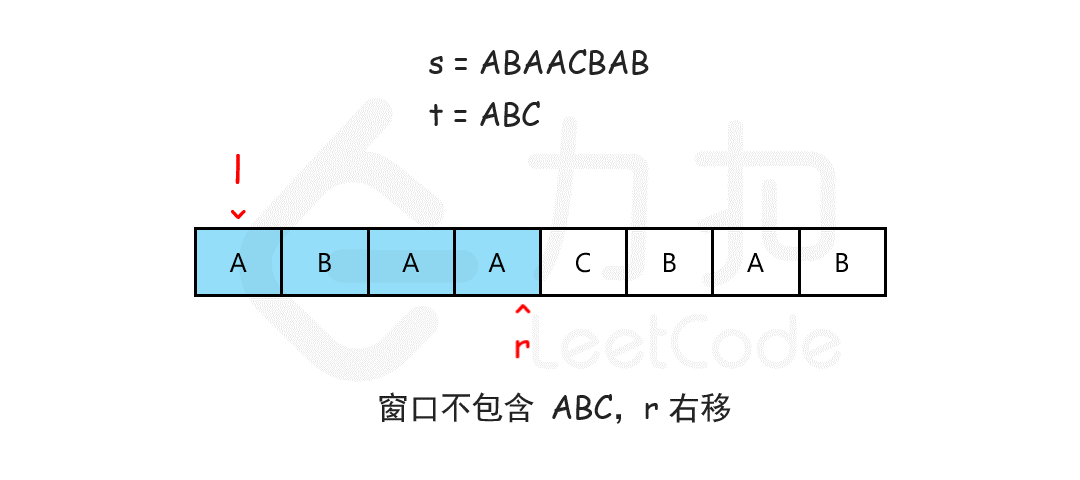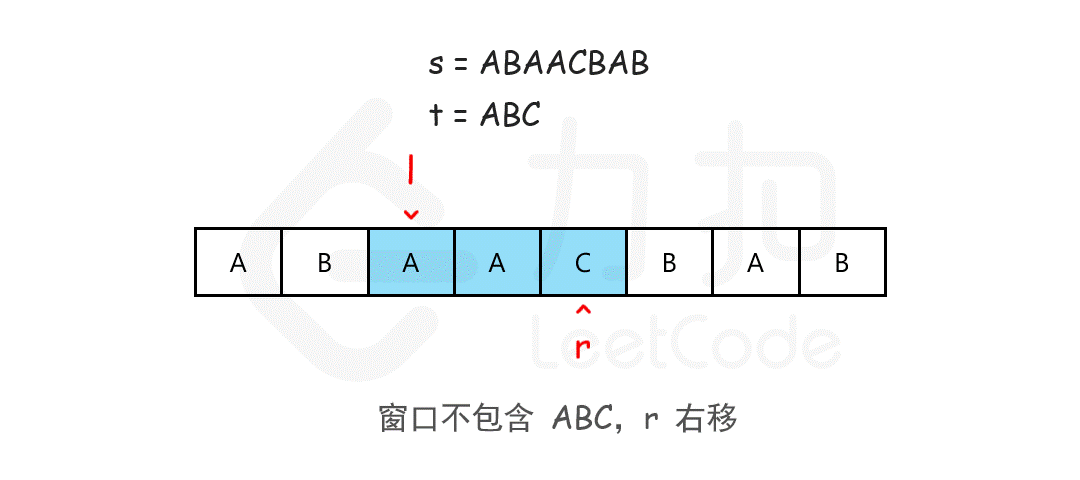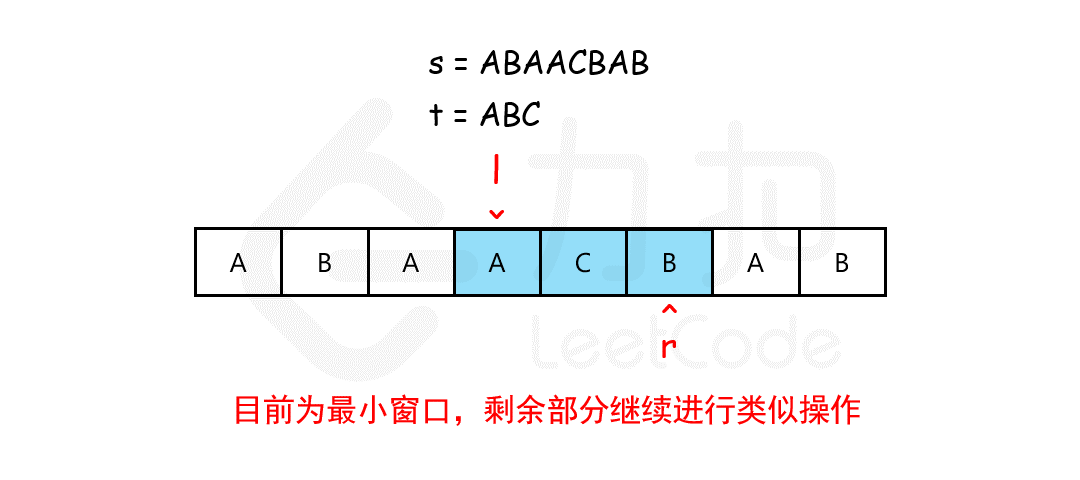
string minWindow(string s, string t) {
if (s.size() < t.size()) return "";
int map[128];
// 遍历字符串 t,初始化每个字母的次数
for (int i = 0; i < t.size(); i++) {
map[t[i]]++;
}
int left = 0; // 左指针
int right = 0; // 右指针
int ans_left = 0; // 保存最小窗口的左边界
int ans_right = -1; // 保存最小窗口的右边界
int ans_len = INT_MAX; // 当前最小窗口的长度
int count = t.size();
// 遍历字符串 s
while (right < s.size()) {
// 当前的字母次数减一
map[s[right]]--;
//代表当前符合了一个字母
if (map[s[right]] >= 0) {
count--;
}
// 开始移动左指针,减小窗口
while (count == 0) { // 如果当前窗口包含所有字母,就进入循环
// 当前窗口大小
int temp_len = right - left + 1;
// 如果当前窗口更小,则更新相应变量
if (temp_len < ans_len) {
ans_left = left;
ans_right = right;
ans_len = temp_len;
}
// 因为要把当前字母移除,所有相应次数要加 1
map[s[left]]++;
//此时的 map[key] 大于 0 了,表示缺少当前字母了,count++
if (map[s[left]] > 0) {
count++;
}
left++; // 左指针右移
}
// 右指针右移扩大窗口
right++;
}
return s.substr(ans_left, ans_len);
}
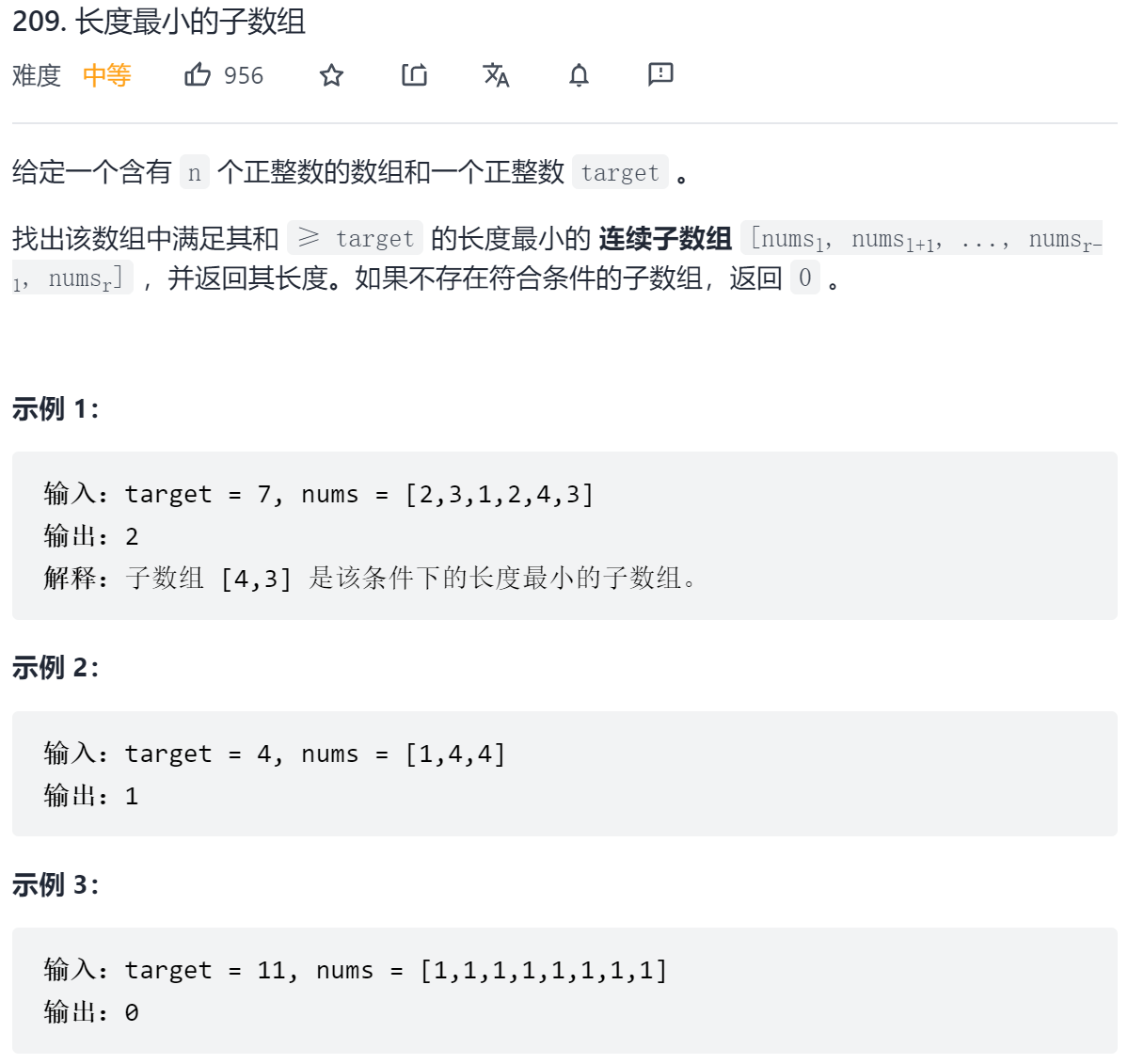
};class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int len = nums.size();
if (len == 0) {return 0;}
int start = 0, end = 0;
int ans = INT_MAX;
int sum = 0;
while (end < len) {
sum += nums[end];
while (sum >= s) {
ans = min(ans, end - start + 1);
sum -= nums[start];
start++;
}
end++;
}
return (ans == INT_MAX)? 0: ans;
}
};这题虽然题目带滑动窗口,但实际与滑动窗口关系不大,这里通过维护一个堆(元素为值和索引)或者双端队列(递减,队首始终为最大值)来解题,当新元素入队列时与队尾比较,如果大于队尾,则队尾元素永远不可能被取为最大值,队尾一直出队直到满足大于入队元素,元素入队后,判断队首元素是否在队列中,如果不在,队首也要出队。这个过程结束后,队首元素即为当前滑动窗口的最大值。
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
if (k == 1) return nums;
// 双端队列,保持队列的递减性,队头元素即为滑动窗口的最大值
deque<int> q;
int n = nums.size();
// 首先将前k个数字挨个入队
// 入队时如果大于队尾元素则将队尾元素出队,说明永远也不可能取到他
for (int i = 0; i < k; i++) {
while (!q.empty() && nums[i] > nums[q.back()]) {
q.pop_back();
}
q.push_back(i);
}
vector<int> res = {nums[q.front()]};
// 其次将k个后的数字挨个入队
for (int i = k; i < n; i++) {
// 入队时如果大于队尾元素则将队尾元素出队,说明永远也不可能取到他
while (!q.empty() && nums[i] > nums[q.back()]) {
q.pop_back();
}
q.push_back(i);
// 将队头的数字出队直到当前滑动窗口有效范围内 (注意!!!!!!!这里判断的是索引)
while (q.front() <= i - k) {
q.pop_front();
}
res.push_back(nums[q.front()]);
}
return res;
}
};此题即对应上面所说的第三种题型,思路一样,维护一个hash表用于保存p的字母个数,滑动窗口解题
class Solution {
public:
vector<int> findAnagrams(string s, string p) {
int n = s.size();
int m = p.size();
// 维护一个hash表用于保存p的字母个数
vector<int> hash(26);
for (auto c : p) {
hash[c - 'a']++;
}
vector<int> res;
for (int l = 0, r = 0; r < n; r++) {
// 每次让r往右走,并减去当前字母一次
hash[s[r] - 'a']--;
// 当遇到不是p的字母或者p的字母减的次数多了,则说明[l, r]不是p的异位词
// 令l右移直到hash表中p的字母恢复到正常情况
while (hash[s[r] - 'a'] < 0) {
hash[s[l] - 'a']++;
l++;
}
// 如果哈希表正常(均大于等于0)并[l, r]长度等于p的长度,则说明[l, r]是p的异位词
if (r - l + 1 == m) res.push_back(l);
}
return res;
}
};通过分别滑动A和B字符串,逐个比对元素是否相同,取相同部分长度返回,最终求最大值
class Solution {
public:
int maxLength(vector<int>& A, vector<int>& B, int addA, int addB, int len) {
int k = 0;
int ans = 0;
// 注意这里的len,不能越界
for (int i = 0; i < len; i++) {
if (A[addA + i] == B[addB + i]) {
k++;
}
else {
k = 0;
}
ans = max(ans, k);
}
return ans;
}
int findLength(vector<int>& A, vector<int>& B) {
int sizeA = A.size(), sizeB = B.size();
int ans = 0;
// 滑动A后取最大的子串长度
for (int i = 0; i < sizeA; i++) {
int len = min(sizeB, sizeA - i);
int tmp = maxLength(A, B, i, 0, len);
ans = max(ans, tmp);
}
// 滑动B后取最大的子串长度
for (int i = 0; i < sizeB; i++) {
int len = min(sizeA, sizeB - i);
int tmp = maxLength(A, B, 0, i, len);
ans = max(ans, tmp);
}
return ans;
}
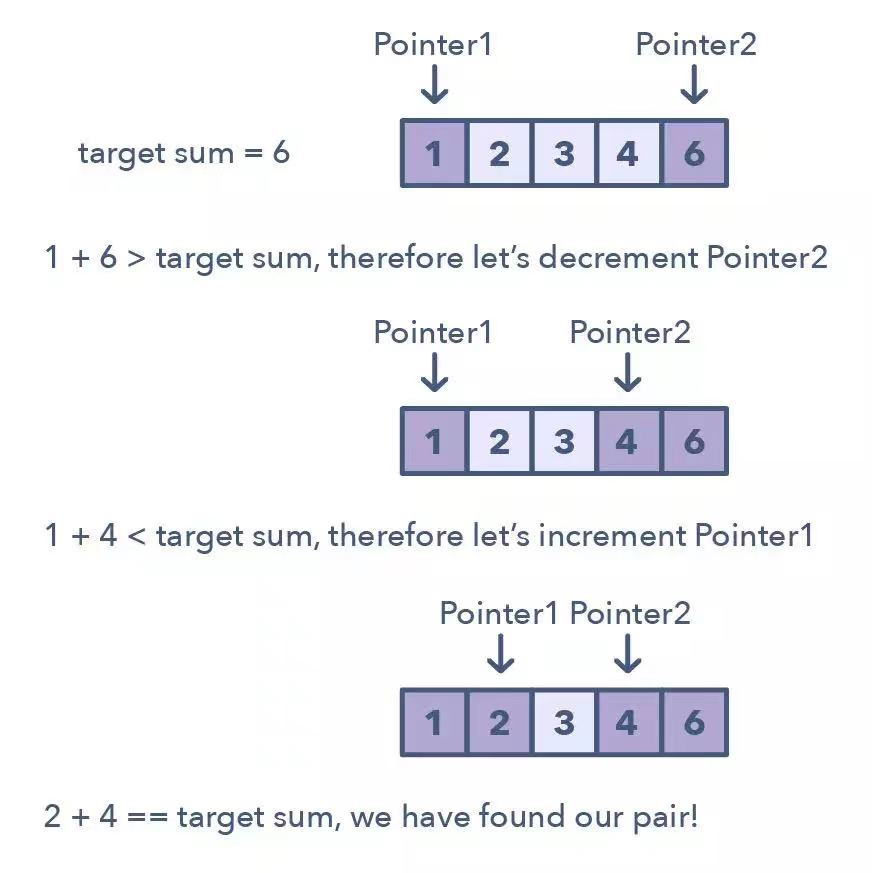
};双指针(Two Pointers)是这样一种模式:两个指针以一前一后的模式在数据结构中迭代,直到一个或两个指针达到某种特定条件。双指针通常在排序数组或链表中搜索配对时很有用;比如当你必须将一个数组的每个元素与其它元素做比较时。
双指针是很有用的,因为如果只有一个指针,你必须继续在数组中循环回来才能找到答案。这种使用单个迭代器进行来回在时间和空间复杂度上都很低效——这个概念被称为「渐进分析(asymptotic analysis)」。尽管使用 1 个指针进行暴力搜索或简单普通的解决方案也有效果,但这会让时间复杂度达到 O(n²) 。在很多情况下,双指针有助于你寻找有更好空间或运行时间复杂度的解决方案。
用于识别使用双指针的时机的方法:
- 可用于你要处理排序数组(或链接列表)并需要查找满足某些约束的一组元素的问题
- 数组中的元素集是配对、三元组甚至子数组
下面是一些满足双指针模式的问题:
- 求一个排序数组的平方(简单)
- 求总和为零的三元组(中等)
- 比较包含回退(backspace)的字符串(中等)
显然,如果数组 nums 中的所有数都是非负数,那么将每个数平方后,数组仍然保持升序;如果数组 nums 中的所有数都是负数,那么将每个数平方后,数组会保持降序。通过找到分界点,给分界点和分界点左边一个作为两个数组的起始点(双指针),后采用归并排序的方法进行结果插入,可以省略排序的时间复杂度,使得时间复杂度达到O(n)。
class Solution {
public:
vector<int> sortedSquares(vector<int>& nums) {
int n = nums.size();
int right= 0;
while (right < n && nums[right] < 0) {
right++;
}
int left = right - 1;
vector<int> res;
while (left >= 0 || right < n) {
int tmp = 0;
if (left < 0) {
tmp = nums[right] * nums[right];
right++;
}
else if (right >= n) {
tmp = nums[left] * nums[left];
left--;
}
else {
if (nums[left] * -1 <= nums[right]) {
tmp = nums[left] * nums[left];
left--;
}
else {
tmp = nums[right] * nums[right];
right++;
}
}
res.push_back(tmp);
}
return res;
}
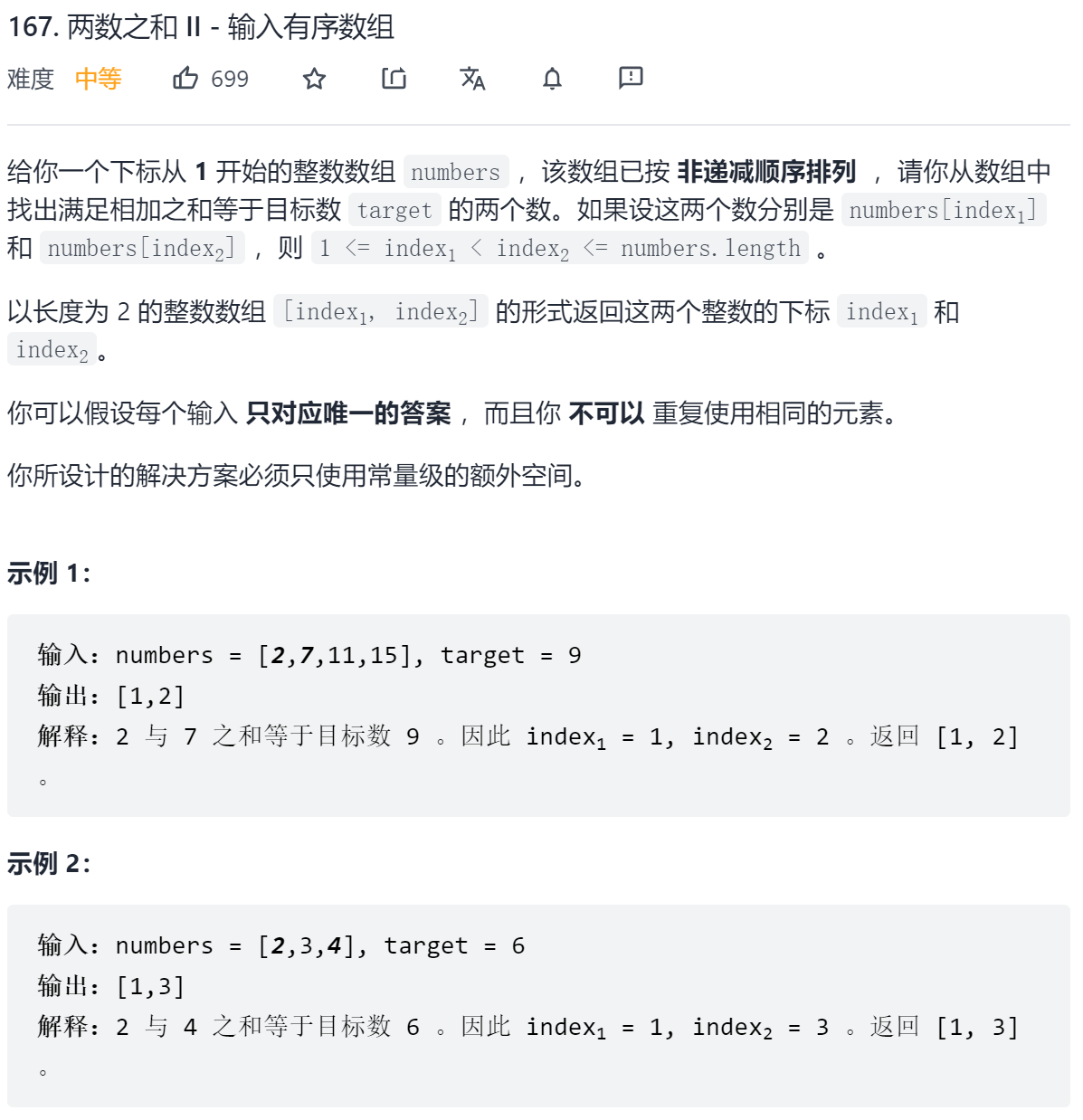
};这题很简单,因为是有序数组,双指针分别从首尾遍历即可,小于目标值说明左边应该变大,左指针右移,大于目标值说明右边应该变小,右指针左移
class Solution {
public:
vector<int> twoSum(vector<int>& numbers, int target) {
int i = 0, j = numbers.size() - 1;
while (i < j) {
if (numbers[i] + numbers[j] == target) {
return {i + 1, j + 1};
}
else if (numbers[i] + numbers[j] < target) {
i++;
}
else {
j--;
}
}
return {};
}
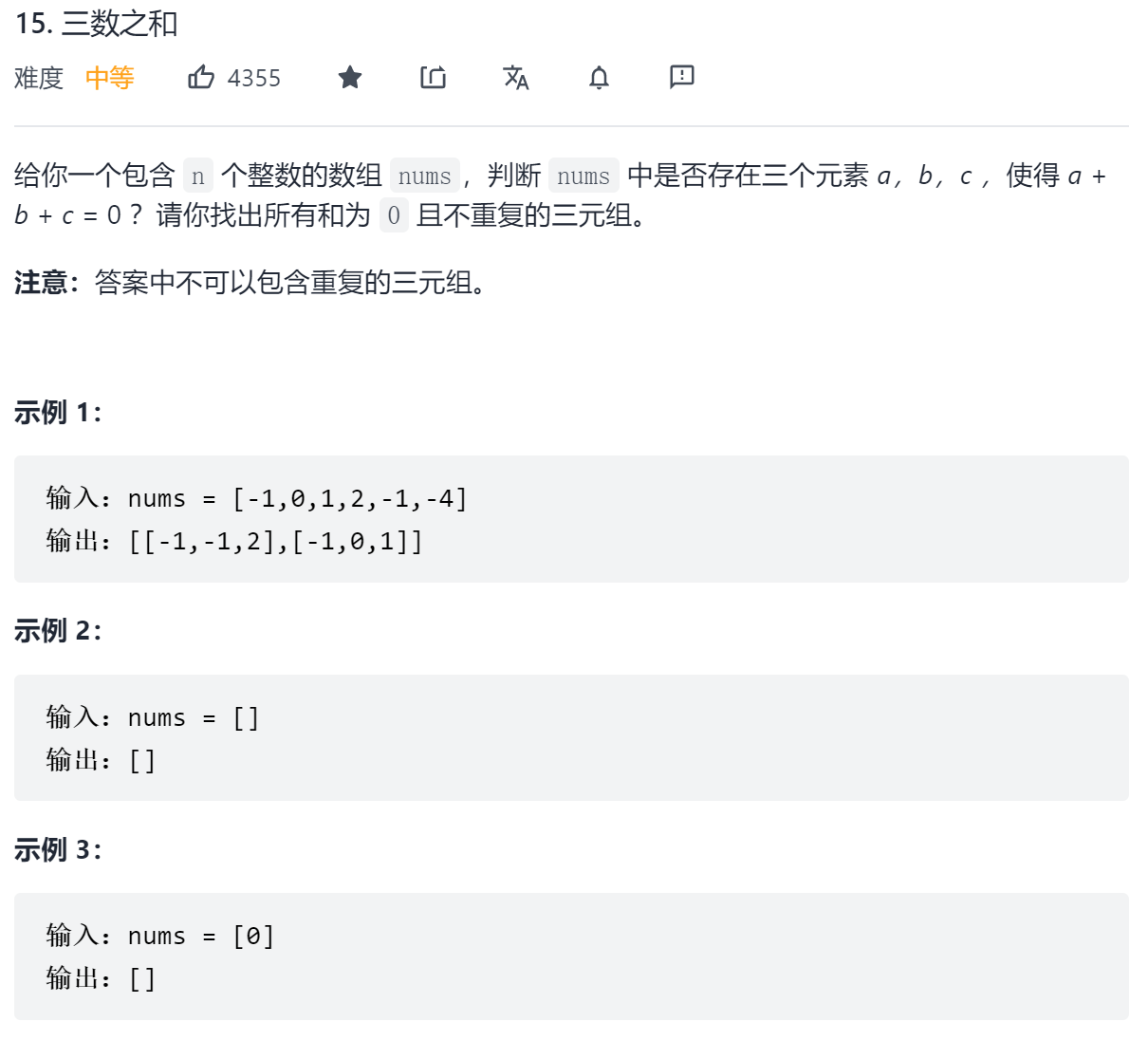
};那么如果是三数之和呢?同样,只需要固定住一个数,然后其余两个数按上面的方法确定即可。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
int len = nums.size();
vector<vector<int>> res;
if (len < 3) return res;
sort(nums.begin(), nums.end());
for (int i = 0; i < len - 2; i++) {
int left = i + 1, right = len - 1, sum = 0 - nums[i];
// 为了保证不加入重复的 list,因为是有序的,所以如果和前一个元素相同,只需要继续后移就可以
if (i == 0 || i > 0 && (nums[i] != nums[i - 1])) {
while (left < right) {
if (nums[left] + nums[right] == sum) {
res.push_back({nums[i], nums[left], nums[right]});
// 元素相同要后移,防止加入重复的list
while (left < right && nums[left] == nums[left + 1]) left++;
while (left < right && nums[right] == nums[right - 1]) right--;
left++; right--;
}
else if (nums[left] + nums[right] < sum) left++;
else right--;
}
}
}
return res;
}
};如果是四数之和呢?与三个数解法类似,不同的是要用双重循环确定前两个数,同时要做一些剪枝操作:
- 在确定第一个数之后,如果 nums[i]+nums[i+1]+nums[i+2]+nums[i+3]>target,说明此时剩下的三个数无论取什么值,四数之和一定大于 target,因此退出第一重循环;
- 在确定第一个数之后,如果 nums[i]+nums[n−3]+nums[n−2]+nums[n−1]<target,说明此时剩下的三个数无论取什么值,四数之和一定小于 target,因此第一重循环直接进入下一轮,枚举 nums[i+1];
- 在确定前两个数之后,如果 nums[i]+nums[j]+nums[j+1]+nums[j+2]>target,说明此时剩下的两个数无论取什么值,四数之和一定大于 target,因此退出第二重循环;
- 在确定前两个数之后,如果 nums[i]+nums[j]+nums[n−2]+nums[n−1]<target,说明此时剩下的两个数无论取什么值,四数之和一定小于 target,因此第二重循环直接进入下一轮,枚举 nums[j+1]。
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
sort(nums.begin(), nums.end());
int n = nums.size();
vector<vector<int>> res;
for (int i = 0; i <= n - 4; i++) {
// 避免重复结果
if (i > 0 && nums[i] == nums[i - 1]) continue;
// 剪枝
if ((long)nums[i] + nums[i+1] + nums[i+2] + nums[i+3] > target) break;
if ((long)nums[i] + nums[n-1] + nums[n-2] + nums[n-3] < target) continue;
for (int j = i + 1; j <= n - 3; j++) {
// 避免重复结果
if (j > i + 1 && nums[j] == nums[j - 1]) continue;
// 剪枝
if ((long)nums[i] + nums[j] + nums[j+1] + nums[j+2] > target) break;
if ((long)nums[i] + nums[j] + nums[n-1] + nums[n-2] < target) continue;
int sum = target - nums[i] - nums[j];
int left = j + 1, right = n - 1;
while (left < right) {
if (nums[left] + nums[right] == sum) {
res.push_back({nums[i], nums[j], nums[left], nums[right]});
// 避免出现重复结果,跳过相同的部分
// 由于循环是找到最后一个相同数字的位置,因此跳出循环后还要右移一次
while (left < right && nums[left] == nums[left+1]) {
left++;
}
left++;
// 避免出现重复结果,跳过相同的部分
// 由于循环是找到最后一个相同数字的位置,因此跳出循环后还要左移一次
while (left < right && nums[right] == nums[right-1]) {
right--;
}
right--;
}
else if (nums[left] + nums[right] > sum) {
right--;
}
else {
left++;
}
}
}
}
return res;
}
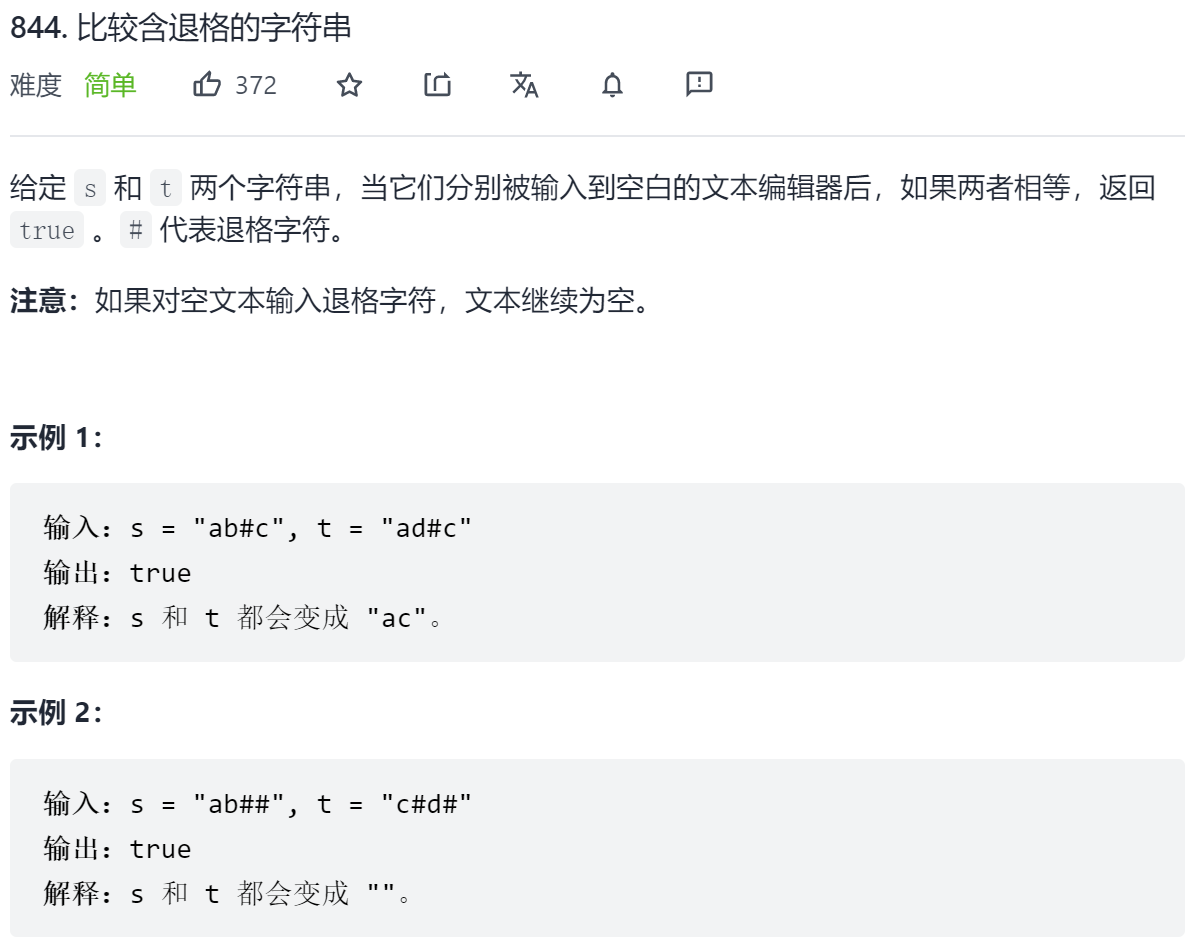
};这一题可以用栈很简单地解决:
class Solution {
public:
bool backspaceCompare(string S, string T) {
return build(S) == build(T);
}
string build(string str) {
string ret;
for (char ch : str) {
if (ch != '#') {
ret.push_back(ch);
} else if (!ret.empty()) {
ret.pop_back();
}
}
return ret;
}
};当然,也可以使用双指针:(比较不直观,建议还是用栈做,时间复杂度都是O(M+N)) 一个字符是否会被删掉,只取决于该字符后面的退格符,而与该字符前面的退格符无关。因此当我们逆序地遍历字符串,就可以立即确定当前字符是否会被删掉。我们定义两个指针,分别指向两字符串的末尾。每次我们让两指针逆序地遍历两字符串,直到两字符串能够各自确定一个字符,然后将这两个字符进行比较。重复这一过程直到找到的两个字符不相等,或遍历完字符串为止。
class Solution {
public:
bool backspaceCompare(string S, string T) {
int i = S.length() - 1, j = T.length() - 1;
int skipS = 0, skipT = 0;
while (i >= 0 || j >= 0) {
while (i >= 0) {
if (S[i] == '#') {
skipS++, i--;
} else if (skipS > 0) {
skipS--, i--;
} else {
break;
}
}
while (j >= 0) {
if (T[j] == '#') {
skipT++, j--;
} else if (skipT > 0) {
skipT--, j--;
} else {
break;
}
}
if (i >= 0 && j >= 0) {
if (S[i] != T[j]) {
return false;
}
} else {
if (i >= 0 || j >= 0) {
return false;
}
}
i--, j--;
}
return true;
}
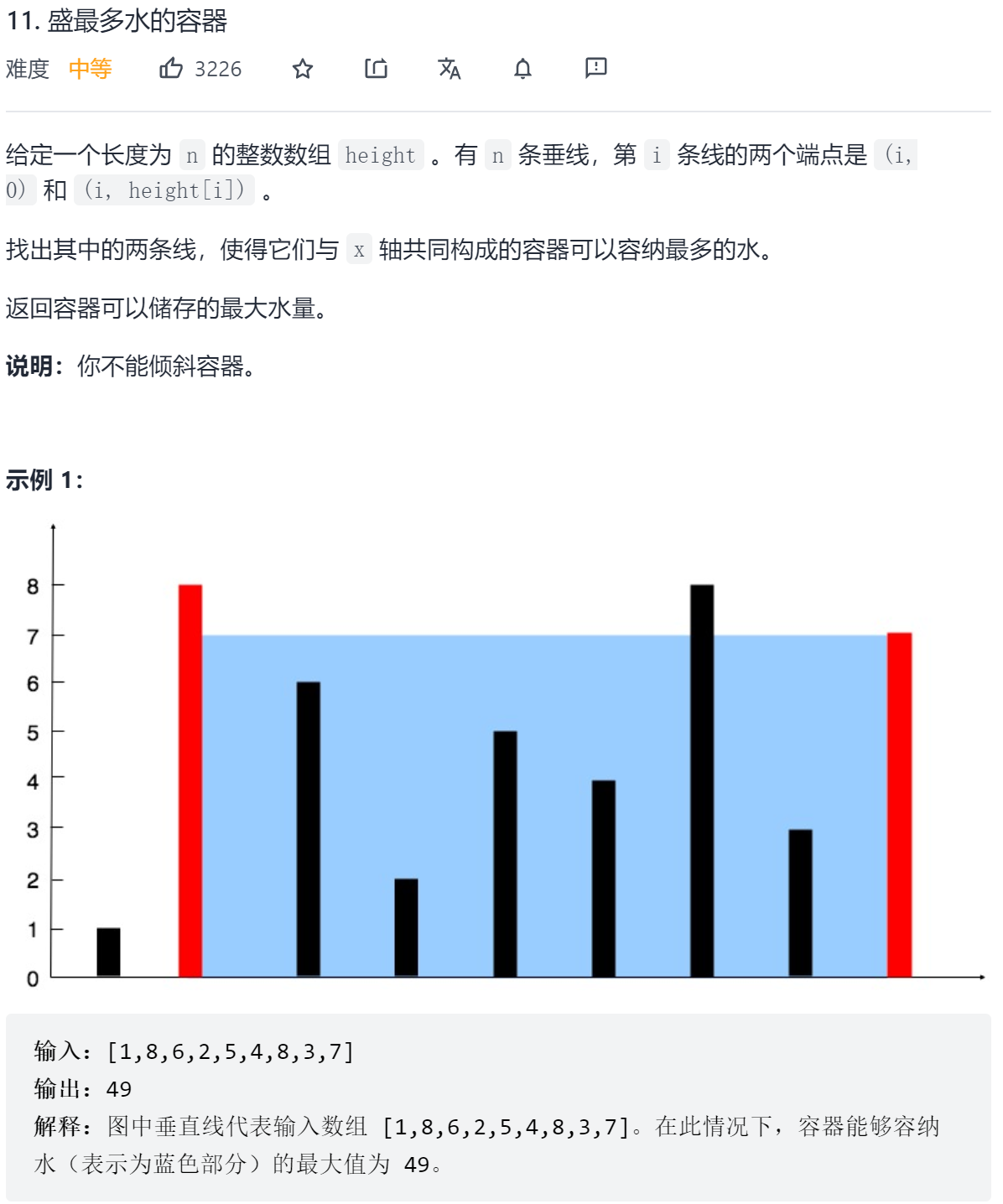
};典型的双指针题,左右分别向中间靠拢,哪边小哪边移动,移动的同时计算盛水的容量,最终取最大值
class Solution {
public:
int maxArea(vector<int>& height) {
int len = height.size();
int res = INT_MIN;
int left = 0, right = len - 1;
while (left < right) {
res = max(res, min(height[left], height[right]) * (right - left));
if (height[left] > height[right]) right--;
else left++;
}
return res;
}
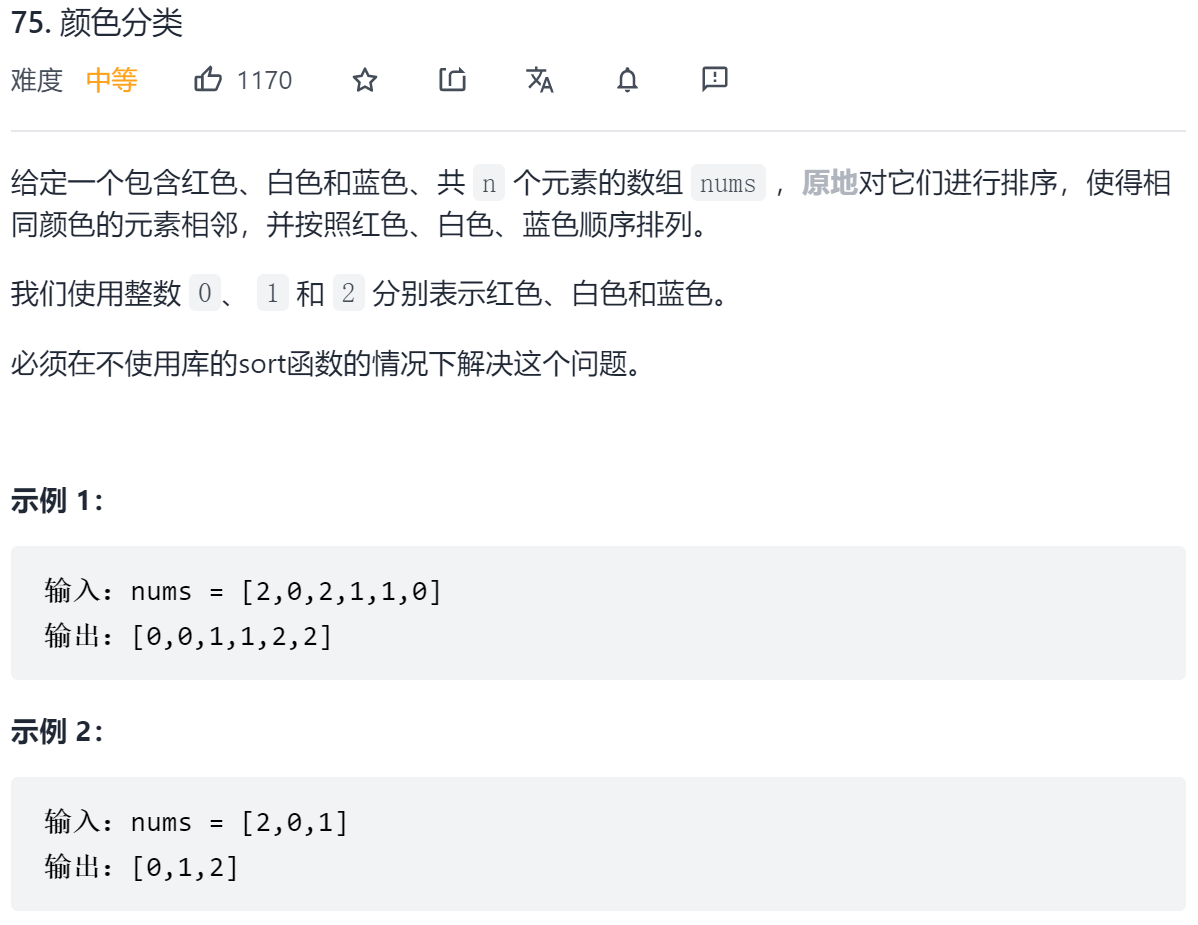
};本题是经典的「荷兰国旗问题」,可以统计出数组中 0, 1, 2 的个数,再根据它们的数量,重写整个数组。这种方法较为简单,也很容易想到。 通过双指针方法,可以达到一遍遍历完成排序的效果。
双指针设立在两头,当遍历到0时,往前交换,左指针右移,当遍历到2时,往后交换,右指针左移,当遍历到右指针位置时,结束遍历。
class Solution {
public:
void sortColors(vector<int>& nums) {
int n = nums.size();
int p0 = 0, p2 = n - 1;
for (int i = 0; i <= p2; ++i) {
while (i <= p2 && nums[i] == 2) {
swap(nums[i], nums[p2]);
--p2;
}
if (nums[i] == 0) {
swap(nums[i], nums[p0]);
++p0;
}
}
}
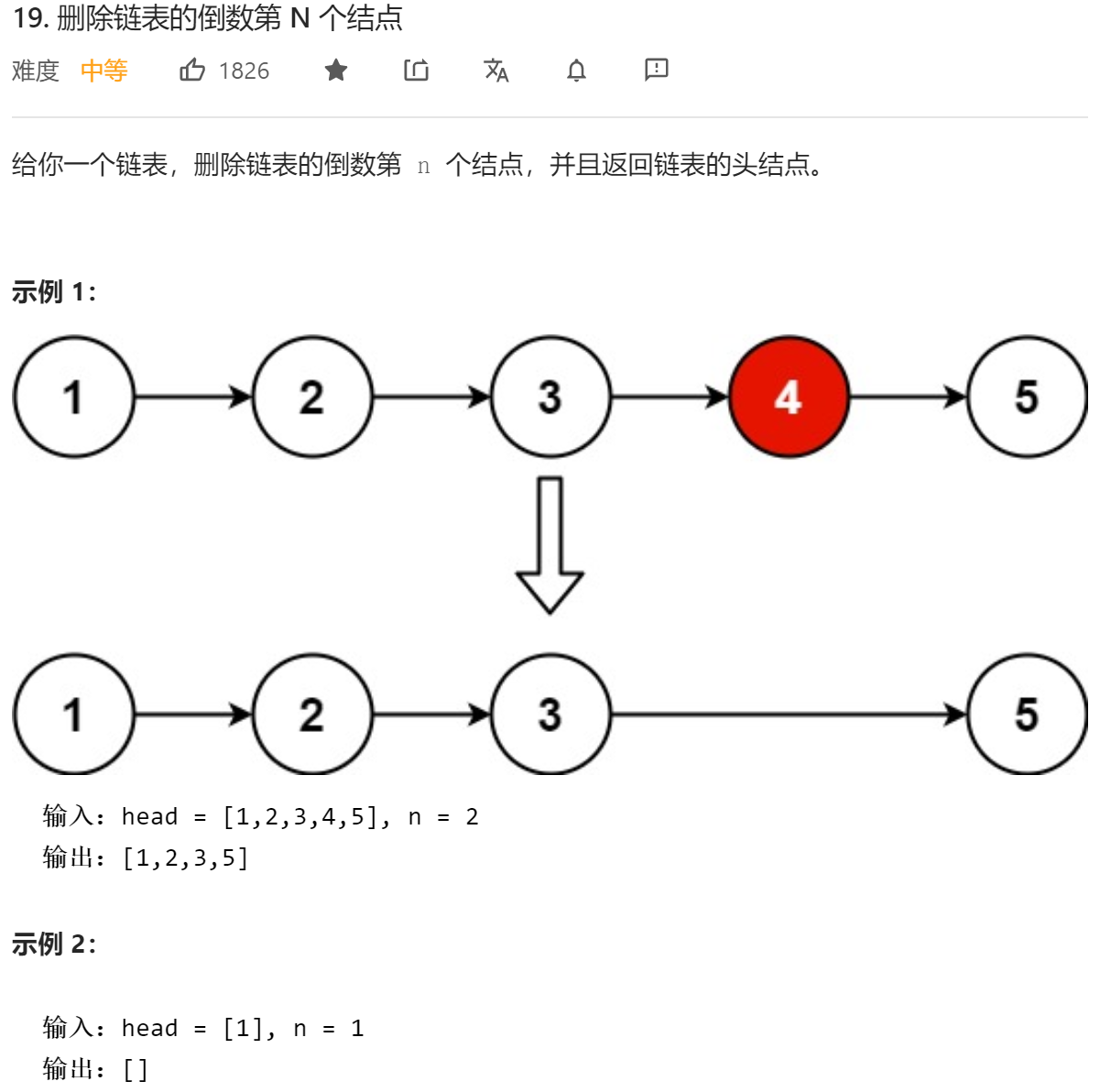
};这一题非常经典,如果不用双指针的话,需要两次遍历,第一次求整个链表的长度,第二次再到指定位置去删除节点。 如果是使用双指针的话,让快指针先走n步,然后快慢指针再同时走,当快指针走到末尾结点时,慢指针即找到待删除节点。这里要考虑只有一个结点的情况,我们将一个新的空结点指向头结点,就可以避免这种情况而不去特殊处理,最终返回这个新结点的下一个结点作为结果,也就避免了头结点被删除的情况
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
// 设置结点指向头结点
ListNode* pre = new ListNode();
pre->next = head;
ListNode* slow = pre;
ListNode* fast = pre;
// 快指针先走
for (int i = 0; i < n; i++) {
fast = fast->next;
}
// 快慢指针同时走,直到快指针到最后
while (fast->next) {
slow = slow->next;
fast = fast->next;
}
// 此时慢指针即是待删除的结点的前一个结点
slow->next = slow->next->next;
return pre->next;
}
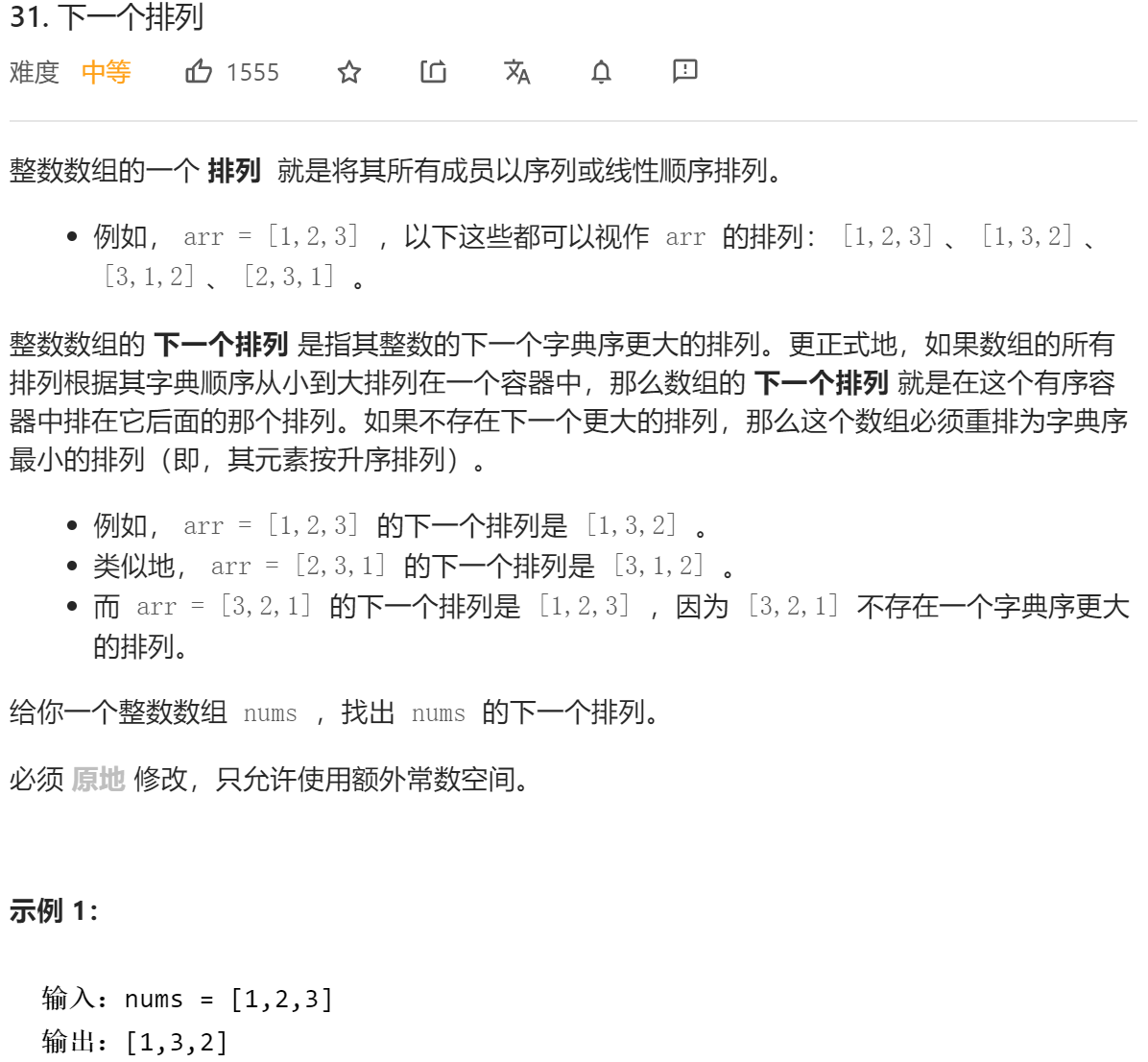
};这个题如果没做过还是相当有难度的,这里直接贴一下官方题解的思路
好像与双指针没太大关系哈。。。
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int i = nums.size() - 2;
// 从后往前找到第一个nums[i] < nums[i + 1]的元素
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--;
}
// 如果i<0则表明整个数组都降序排列
if (i >= 0) {
int j = nums.size() - 1;
// 在区间[i+1:]找到第一个大于nums[i]的元素
// 这里没有令j >= i+1,因为区间[i+1:]降序排列,所以一定能在这个区间内找到大于nums[i]的元素
while (j >= 0 && nums[i] >= nums[j]) {
j--;
}
// 交换这两个数
swap(nums[i], nums[j]);
}
// 反转降序的部分
reverse(nums.begin() + i + 1, nums.end());
}
};这个题目有两种思路:
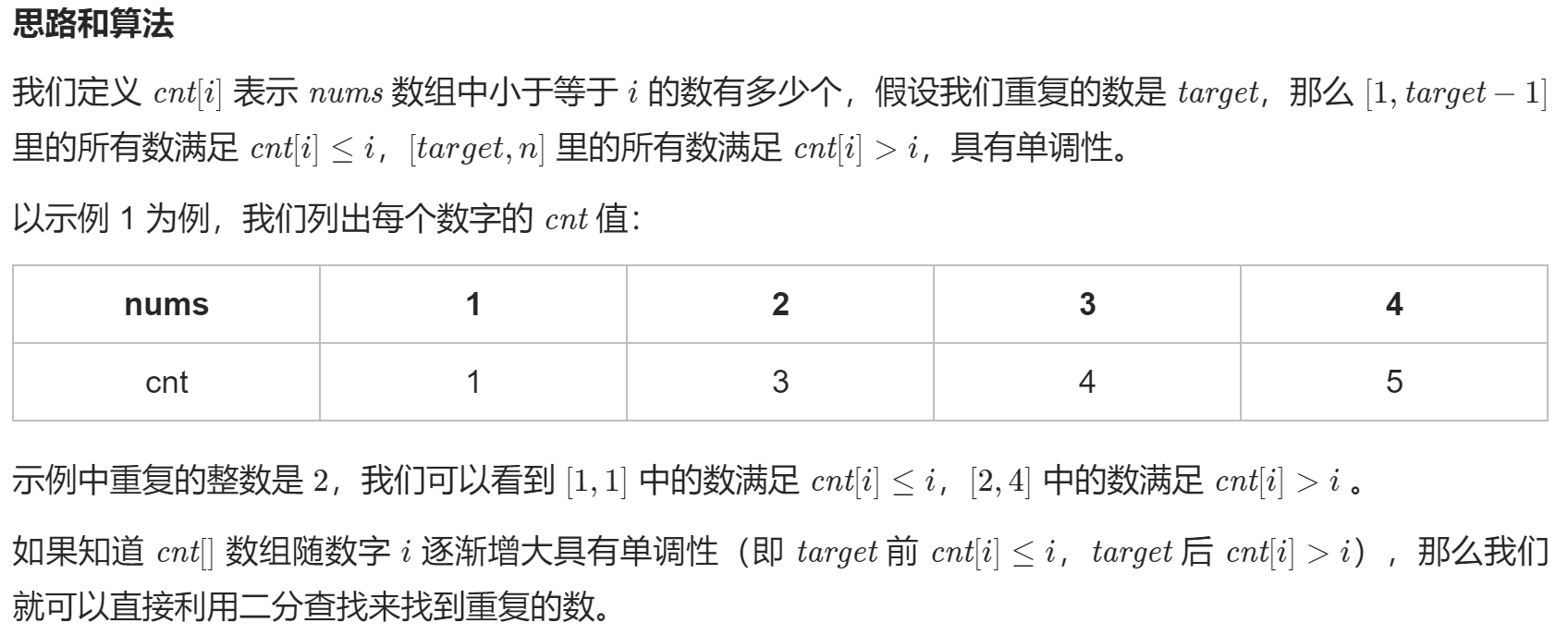
- 二分法:
时间复杂度:O(nlogn),其中 nn 为 nums 数组的长度。O(logn) 代表了我们枚举二进制数的位数个数,枚举第 i 位的时候需要遍历数组统计 x 和 y 的答案,因此总时间复杂度为 O(nlogn)。
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int n = nums.size();
int l = 1, r = n - 1, ans = -1;
while (l <= r) {
int mid = (l + r) >> 1;
// 统计小于等于mid的个数
int cnt = 0;
for (int i = 0; i < n; ++i) {
cnt += nums[i] <= mid;
}
if (cnt <= mid) {
l = mid + 1;
} else {
r = mid - 1;
ans = mid;
}
}
return ans;
}
};- 双指针(快慢):
这里就依赖于对 「Floyd 判圈算法」(又称龟兔赛跑算法)有所了解,它是一个检测链表是否有环的算法,LeetCode 中相关例题有 141. 环形链表,142. 环形链表 II。
我们对 nums 数组建图,每个位置 i 连一条 i→nums[i] 的边。由于存在的重复的数字 target,因此 target 这个位置一定有起码两条指向它的边,因此整张图一定存在环,且我们要找到的 target 就是这个环的入口,那么整个问题就等价于 142. 环形链表 II。
我们先设置慢指针 slow 和快指针 fast ,慢指针每次走一步,快指针每次走两步,根据「Floyd 判圈算法」两个指针在有环的情况下一定会相遇,此时我们再将 slow 放置起点 0,两个指针每次同时移动一步,相遇的点就是答案。
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int slow = 0, fast = 0;
// 从头开始,慢指针每次走一步,快指针每次走两步直到相遇
do {
slow = nums[slow];
fast = nums[nums[fast]];
} while (slow != fast);
// 将慢指针设回开头位置
slow = 0;
// 此时再将两个指针每次同时移动一步,相遇的点就是环入口
while (slow != fast) {
slow = nums[slow];
fast = nums[fast];
}
return slow;
}
};这个题目通过快慢指针实现二分,然后将两部分进行归并排序,很巧妙
class Solution {
public:
ListNode* mergeSort(ListNode* head1, ListNode* head2) {
ListNode* start = new ListNode();
ListNode* ans = start;
while (head1 && head2) {
if (head1->val < head2->val) {
start->next = head1;
start = start->next;
head1 = head1->next;
}
else {
start->next = head2;
start = start->next;
head2 = head2->next;
}
}
if (!head1) {
while (head2) {
start->next = head2;
start = start->next;
head2 = head2->next;
}
}
if (!head2) {
while (head1) {
start->next = head1;
start = start->next;
head1 = head1->next;
}
}
return ans->next;
}
ListNode* sortList(ListNode* head) {
if (head == nullptr || head->next == nullptr) return head;
ListNode* start = new ListNode();
start->next = head;
ListNode* slow = start;
ListNode* fast = start;
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
}
ListNode* right_head = slow->next;
slow->next = nullptr;
ListNode* h1 = sortList(head);
ListNode* h2 = sortList(right_head);
return mergeSort(h1, h2);
}
};又是很巧妙的一种双指针解法,当一条路径遍历完后让其从另一条路径开始,这样会让第二次遍历时在交点处相遇。
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* a = headA;
ListNode* b = headB;
while (a != b) {
a = a == nullptr? headB: a->next;
b = b == nullptr? headA: b->next;
}
return a;
}
};遍历到每个单词的起止位置,用双指针反转字符串即可。
class Solution {
public:
string reverseWords(string s) {
int length = s.length();
int i = 0;
while (i < length) {
int start = i;
// 遍历到单词结束的空格位置
while (i < length && s[i] != ' ') {
i++;
}
// 反转字符串
int left = start, right = i - 1;
while (left < right) {
swap(s[left], s[right]);
left++;
right--;
}
// 将单词后面的空格走完
while (i < length && s[i] == ' ') {
i++;
}
}
return s;
}
};很经典的一道题,如果想要空间复杂度为O(1)的话,则需要用的双指针算法(快慢指针),具体流程为:
- 快慢指针找到中点
- 以中点为界分成两个链表
- 反转其中一个链表
- 双指针依次判断这两个链表是否一一对应相等
class Solution {
public:
bool isPalindrome(ListNode* head) {
// 快慢指针找中点
ListNode* slow = head;
ListNode* fast = head;
while (fast != nullptr && fast->next != nullptr) {
slow = slow->next;
fast = fast->next->next;
}
// 反转链表
ListNode* new_head = reverseList(slow);
// 一一对应是否相等
while (head && new_head) {
if (head->val != new_head->val) {
return false;
}
head = head->next;
new_head = new_head->next;
}
return true;
}
ListNode* reverseList(ListNode* head) {
if (head == nullptr) return head;
ListNode* pre = nullptr;
while (head) {
ListNode* tmp = head->next;
head->next = pre;
pre = head;
head = tmp;
}
return pre;
}
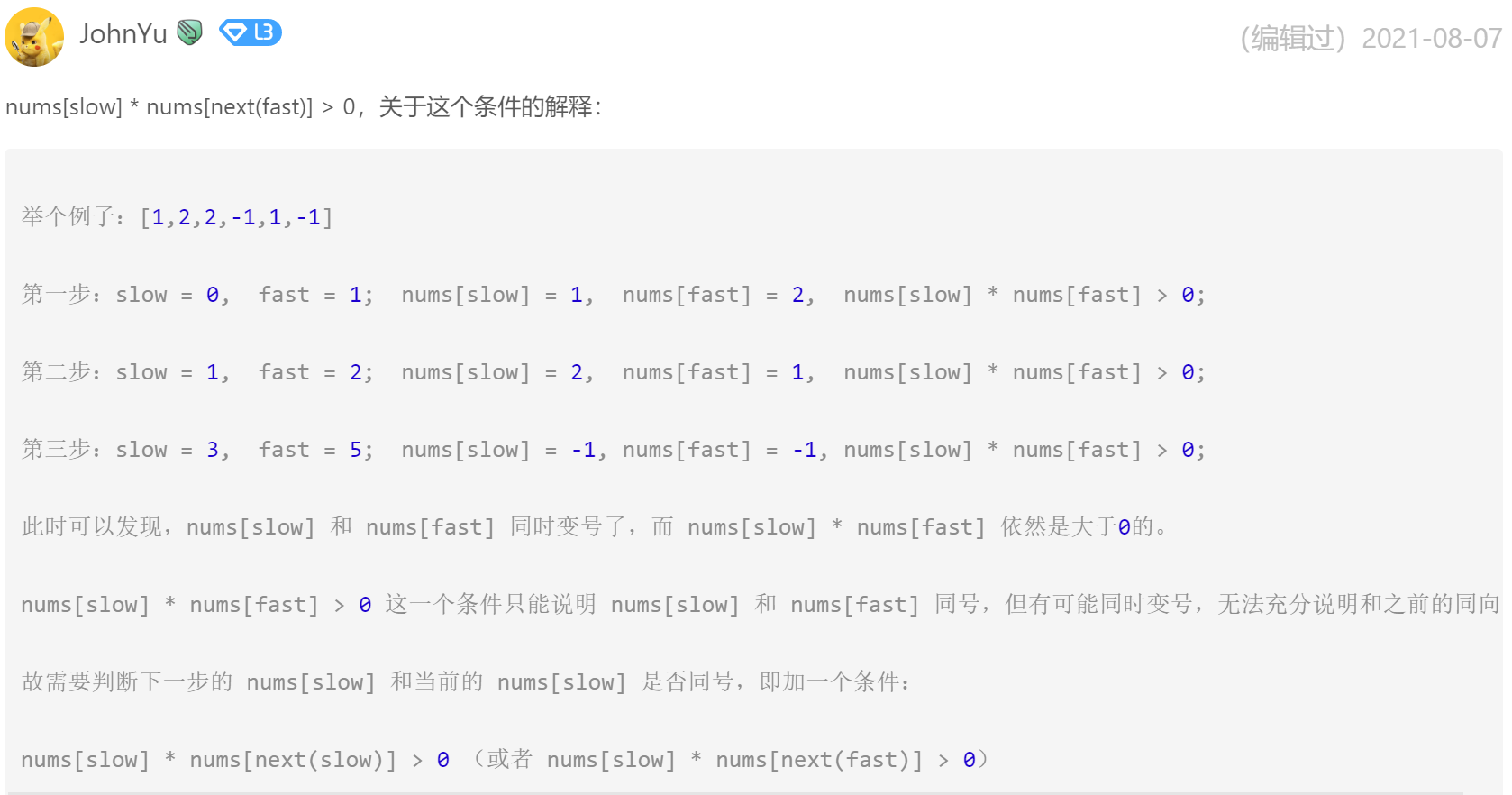
};这是快慢指针十分典型的题目,循环数组类型,但由于题目条件较为复杂,要求循环路径只能同向,因此需要进行一些限制
class Solution {
public:
bool circularArrayLoop(vector<int>& nums) {
int n = nums.size();
auto next = [&](int i) {
return ((i + nums[i]) % n + n) % n;
};
for (int i = 0; i < n; i++) {
int slow = i;
int fast = next(i);
// 每一步都要满足题目的要求,循环路径同向
// 注意,这里如果不加nums[slow] * nums[next(fast)] > 0
// 由于快指针一次走两步,可能会导致某些异号的情况漏掉,具体见下面评论
// 或者写成nums[slow]*nums[next(slow)] > 0 && nums[fast]*nums[next(fast)] > 0也可行
while (nums[slow] * nums[fast] > 0 && nums[slow] * nums[next(fast)] > 0) {
// 快慢指针相遇,说明存在环
if (slow == fast) {
// 如果slow == next(slow),说明环的长度为1
if (slow == next(slow)) break;
// 否则说明找到环了
else return true;
}
// 快慢指针移动
slow = next(slow);
fast = next(next(fast));
}
// 当没找到环并且轨迹反向时,说明i作为起点这条路不通
// 可以将这条路上同向的部分设置成0,保证后面不再走这条同向的路
// 起到了剪枝的效果
int tmp = i;
while (nums[tmp] * nums[next(tmp)] > 0) {
int num = tmp;
tmp = next(num);
nums[num] = 0;
}
}
return false;
}
};这里贴两个解释,为什么循环条件要加上nums[slow] * nums[next(fast)] > 0:
合并区间模式是一种处理重叠区间的有效技术。在很多涉及区间的问题中,你既需要找到重叠的区间,也需要在这些区间重叠时合并它们。该模式的工作方式为:
给定两个区间(a 和 b),这两个区间有 6 种不同的互相关联的方式:
理解并识别这六种情况有助于你求解范围广泛的问题,从插入区间到优化区间合并等。
那么如何确定何时该使用合并区间模式呢?
如果你被要求得到一个仅含互斥区间的列表
如果你听到了术语「重叠区间(overlapping intervals)」
合并区间模式的问题:
-
区间交叉(中等)
-
最大 CPU 负载(困难)
注意要先按区间头点排序,再合并
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if (intervals.size() == 0) {
return {};
}
sort(intervals.begin(), intervals.end());
vector<vector<int>> merged;
for (int i = 0; i < intervals.size(); ++i) {
int L = intervals[i][0], R = intervals[i][1];
if (!merged.size() || merged.back()[1] < L) {
merged.push_back({L, R});
}
else {
merged.back()[1] = max(merged.back()[1], R);
}
}
return merged;
}
};这里需要注意处理插入的条件,还有最后的部分,如果没有插入要记得插入
class Solution {
public:
vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int>& newInterval) {
int n = intervals.size();
vector<vector<int>> res;
if (n == 0) return {newInterval};
int left = newInterval[0], right = newInterval[1];
bool placed = false; // 记录新区间有没有插入
for (int i = 0; i < n; i++) {
// 由于intervals是升序排列
// 当intervals[i][0] > right时,说明后面都比right大
// 如果没插入left right, 此时应该插入left right
// 否则插入intervals[i]
if (intervals[i][0] > right) {
if (!placed) {
res.push_back({left, right});
placed = true;
}
res.push_back(intervals[i]);
}
if (intervals[i][1] < left) {
res.push_back(intervals[i]);
}
else {
left = min(intervals[i][0], left);
right = max(intervals[i][1], right);
}
}
// 这里不能忘记,如果遍历到最后都没有插入leftright,需要插入
if (!placed) {
res.push_back({left, right});
}
return res;
}
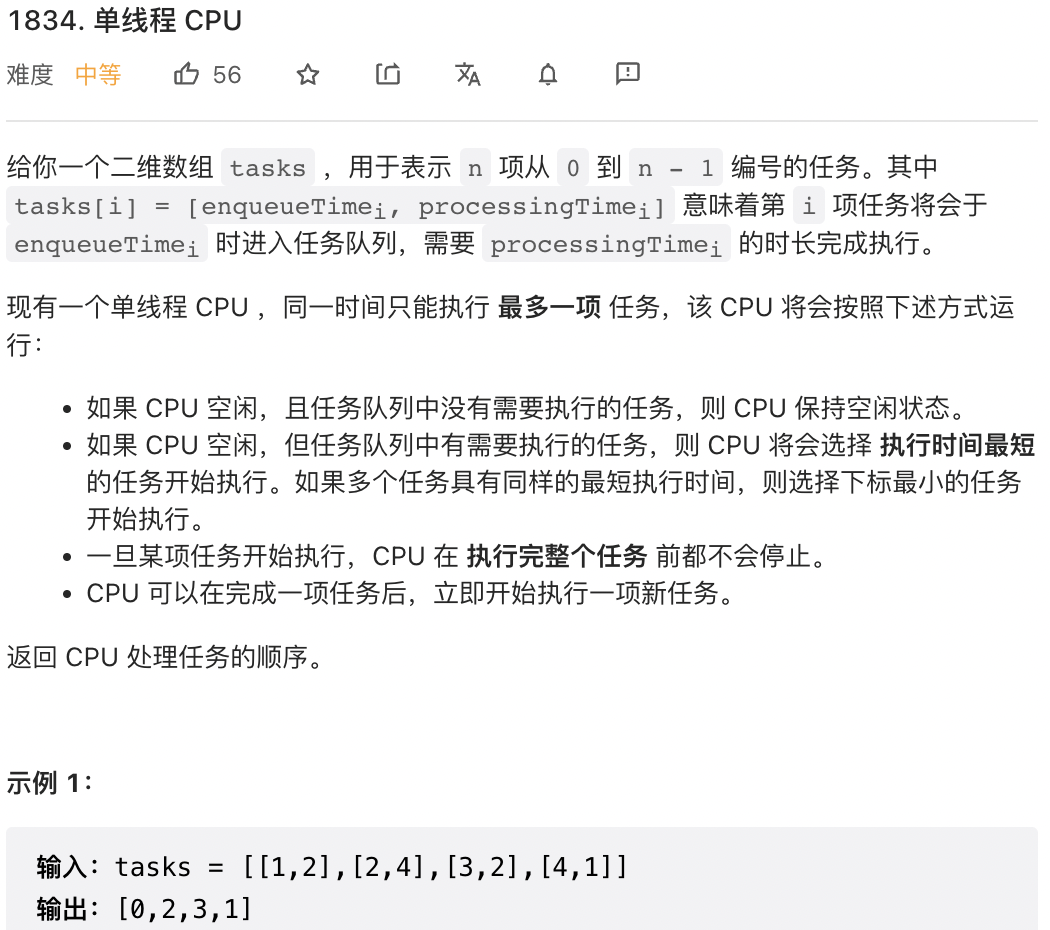
};class Solution {
public:
vector<int> getOrder(vector<vector<int>>& tasks) {
int n = tasks.size();
// 创建小顶堆
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
// index用于存储排序后的task索引位置
vector<int> index(n);
// 从0开始逐步加1赋初始值
iota(index.begin(), index.end(), 0);
// 排序
sort(index.begin(), index.end(), [&](int i, int j) {
return tasks[i][0] < tasks[j][0];
});
vector<int> res;
// 下次任务要执行的时间
long long t = 0;
// 遍历index的指针
int ptr = 0;
while (res.size() != n) {
// 当堆为空时,说明没有待执行的任务,快进到下一次可执行的任务
if (q.empty()) {
t = max(t, (long long)tasks[index[ptr]][0]);
}
// 当有任务执行时,将本次任务执行完前的其他任务入堆
while (ptr < n && tasks[index[ptr]][0] <= t) {
q.push(make_pair(tasks[index[ptr]][1], index[ptr]));
ptr++;
}
// 选择处理时间最小的任务
t += q.top().first;
res.push_back(q.top().second);
q.pop();
}
return res;
}
};最小的k个数
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
vector<int> vec(k, 0);
if (k == 0) { // 排除 0 的情况
return vec;
}
// 默认为大顶堆,即less
priority_queue<int> Q;
for (int i = 0; i < k; ++i) {
Q.push(arr[i]);
}
for (int i = k; i < (int)arr.size(); ++i) {
// 入过k个数之后,如果还堆顶的数大于要入堆的数,则先把堆顶的数出堆
if (Q.top() > arr[i]) {
Q.pop();
Q.push(arr[i]);
}
}
for (int i = 0; i < k; ++i) {
vec[i] = Q.top();
Q.pop();
}
return vec;
}
};其他的方法还包括快排思想(只排前k个)、计数排序(o(n))等,见此链接
在有序的数组或者链表中,找到某个分界点,可以套用二分法,将时间复杂度降低到O(logN) 注意二分条件,最终结果会落到left+1,要取分界点为左边均不满足结果,右边可以满足结果
class Solution {
public:
int findKthPositive(vector<int>& arr, int k) {
int n = arr.size();
int left = 0, right = n - 1;
while (left <= right) {
int mid = (left + right) / 2;
// 可知arr[mid] - mid - 1就是arr[mid]处缺失的整数个数
// 这里的目的是找到第一个大于或等于K的位置
if (arr[mid] - mid - 1 < k)
left = mid + 1;
else
right = mid - 1;
}
// 化简 arr[left - 1] + k - (arr[left - 1] - (left - 1) - 1) 而来
// 可以避免left = 0时出错
return k + left;
}
};class Solution {
public:
bool check(vector<vector<int>>& matrix, int k, int mid, int n) {
int num = 0;
int i = n - 1;
int j = 0;
// 沿着边界走,同时统计左上角矩阵元素的个数
while (i >= 0 && j < n) {
// 往右走
if (matrix[i][j] <= mid) {
num += i + 1; // 注意这里右走一格加一竖列的个数
j++;
}
// 往上走
else {
// num += j;
i--;
}
}
// cout << mid << " | " << num << endl;
return num < k; // 这里不能带等号,带了会导致取mid无限循环
}
int kthSmallest(vector<vector<int>>& matrix, int k) {
int n = matrix.size();
int left = matrix[0][0];
int right = matrix[n-1][n-1];
while (left < right) {
// cout << left << " and " << right << endl;
int mid = (left + right) / 2;
// mid为界限划分矩阵,左上角小于等于mid,右下角大于mid
// 统计左上角个数,如果小于k,说明第k小的数大于mid
// 否则第k小的数小于等于mid
if (check(matrix, k, mid, n)) {
left = mid + 1;
}
else {
right = mid;
}
}
return left;
}
};Tree DFS 是基于深度优先搜索(DFS)技术来遍历树。
你可以使用递归(或该迭代方法的技术栈)来在遍历期间保持对所有之前的(父)节点的跟踪。
Tree DFS 模式的工作方式是从树的根部开始,如果这个节点不是一个叶节点,则需要做三件事:
1.决定现在是处理当前的节点(pre-order),或是在处理两个子节点之间(in-order),还是在处理两个子节点之后(post-order) 2. 为当前节点的两个子节点执行两次递归调用以处理它们
如何识别 Tree DFS 模式:
- 如果你被要求用 in-order、pre-order 或 post-order DFS 来遍历一个树
- 如果问题需要搜索其中节点更接近叶节点的东西
Tree DFS 模式的问题:
- 路径数量之和(中等)
- 一个和的所有路径(中等)
- 递归版本很简单:
class Solution {
public:
void inorder(TreeNode* root, vector<int>& res) {
if (!root) {
return;
}
inorder(root->left, res);
res.push_back(root->val);
inorder(root->right, res);
}
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
inorder(root, res);
return res;
}- 迭代版本(使用栈)相对复杂一点:
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
if (!root) return res;
stack<TreeNode*> s;
// 左边进栈到底
while(root || !s.empty()) { // !s.empty()保证了在root为空时还能取栈顶节点
while(root) {
s.push(root);
root = root->left;
}
// 栈顶出栈
auto& top = s.top();
s.pop();
res.push_back(top->val);
// 往右遍历,但是循环中还是会从左边进栈到底
root = top->right;
}
return res;
}
};后序遍历对于迭代算法来说更加复杂一些,需要记录前一个输出的节点,并判断右子树的状态来确定是输出当前结点还是先遍历右子树。
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
// 迭代写法
vector<int> res;
// 用于记录上一个加入res的节点
TreeNode* pre = nullptr;
stack<TreeNode*> stk;
while (root || !stk.empty()) {
// 往左孩子走到底
while (root) {
stk.emplace(root);
root = root->left;
}
root = stk.top();
// 判断最左节点的右孩子是否为空,若为空,则说明需要输出
// 或者存在右孩子且已经输出完了,输出当前节点
if (!root->right || root->right == pre) {
res.emplace_back(root->val);
// 记录当前输出的节点
pre = root;
// 将当前节点置为空,方便下一次循环取栈顶节点
root = nullptr;
}
// 如果当前节点右孩子不为空,且还没有输出右子树部分
// 否则往右走一次,再通过顶层循环继续往左走到底,按后序遍历进栈
else {
root = root->right;
}
}
return res;
}
};class Solution {
public:
bool isSubStructure(TreeNode* A, TreeNode* B) {
if (A == nullptr || B == nullptr) return false;
// 先序遍历时,首先判断以A为根节点的子树是否包含B
// 如果是,后面就不用继续递归了,所以使用||
return recur(A, B) || isSubStructure(A->left, B) || isSubStructure(A->right, B);
}
// 此函数用于判断以A为根节点的子树是否包含B
bool recur(TreeNode* A, TreeNode* B) {
// 如果B遍历到空指针了,说明前面都相等了,返回true
if (B == nullptr) return true;
// 如果AB的值不同,说明是不同的子结构
// 注意,这里需要添加A是否是空指针的判断
if (A == nullptr || A->val != B->val) return false;
// 如果AB值相同,继续递归判断其左右子树
return recur(A->left, B->left) && recur(A->right, B->right);
}
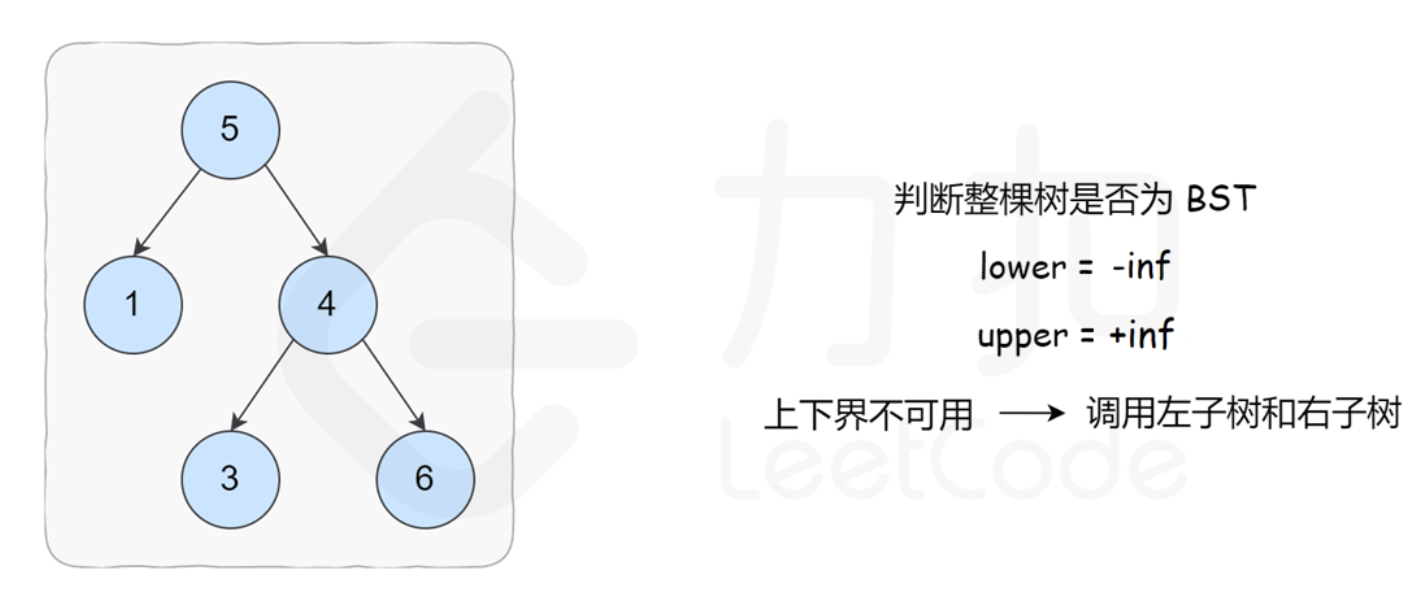
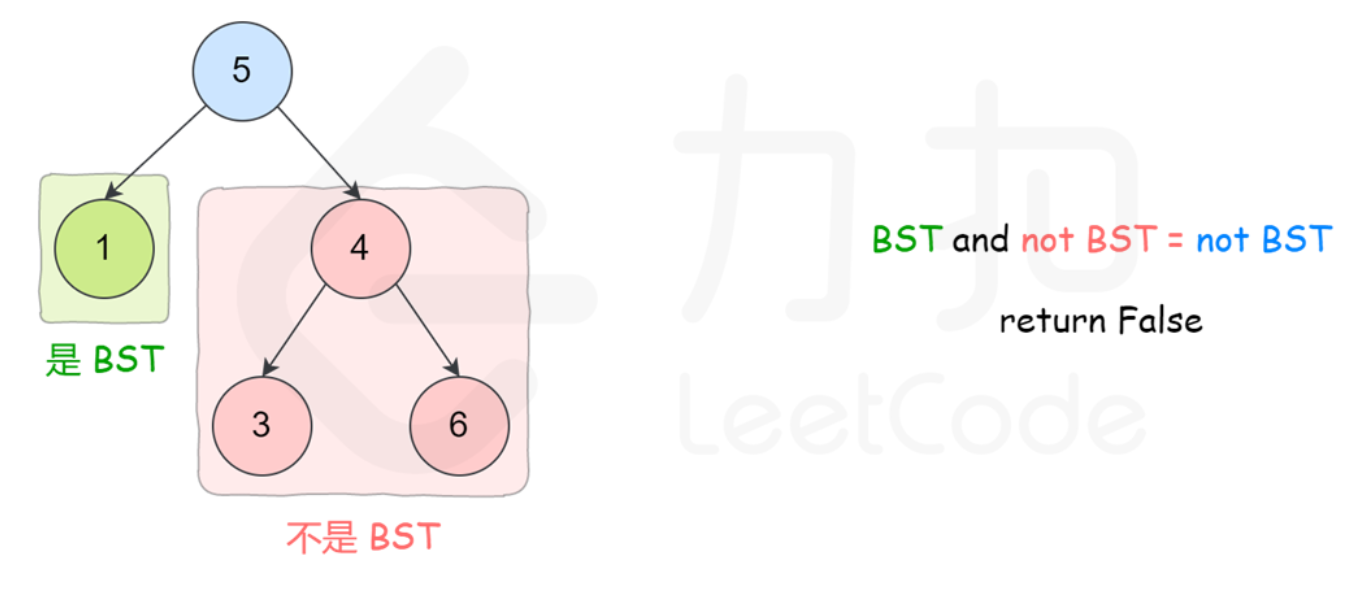
};- DFS递归
class Solution {
public:
bool dfs(TreeNode* root, const long& low, const long& high) {
if (!root) return true;
if (root->val <= low || root->val >= high) return false;
return dfs(root->left, low, root->val) && dfs(root->right, root->val, high);
}
bool isValidBST(TreeNode* root) {
return dfs(root, LONG_MIN, LONG_MAX);
}
};- 中序遍历
根据二叉搜索树的性质可知,中序遍历的结果一定是升序的,如果出现了上一个遍历到的值大于当前遍历到的值,则说明不是AVL
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> stack;
long long inorder = (long long)INT_MIN - 1;
while (!stack.empty() || root != nullptr) {
while (root != nullptr) {
stack.push(root);
root = root -> left;
}
root = stack.top();
stack.pop();
// 如果中序遍历得到的节点的值小于等于前一个 inorder,说明不是二叉搜索树
if (root -> val <= inorder) {
return false;
}
inorder = root -> val;
root = root -> right;
}
return true;
}
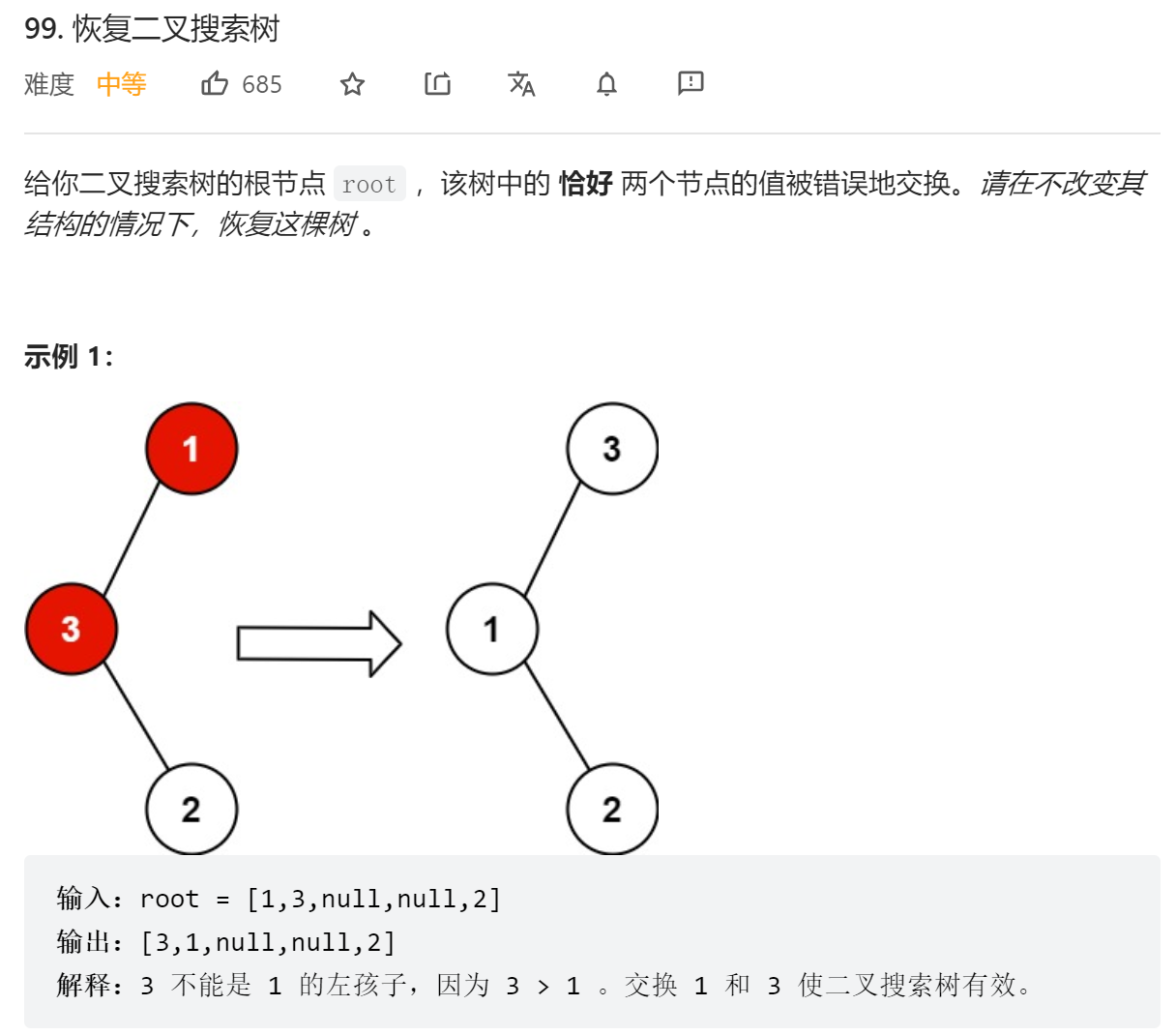
};与上一题相同,二叉搜索树中序遍历结果一定是递增的,如果有两个数被交换,那么一定存在非递增的部分: 注意如果是中序遍历相邻的两个节点交换位置的话,只有一个数ai > ai+1,否则会有两个数ai > ai+1,aj > aj+1
class Solution {
public:
void recoverTree(TreeNode* root) {
stack<TreeNode*> stk;
TreeNode* x = nullptr;
TreeNode* y = nullptr;
TreeNode* pred = nullptr;
while (!stk.empty() || root != nullptr) {
while (root != nullptr) {
stk.push(root);
root = root->left;
}
root = stk.top();
stk.pop();
// 当root值小于前一个值时,说明这个数有问题
if (pred != nullptr && root->val < pred->val) {
// 因为如果存在不相邻的两个位置时,是要记录i和j+1的
// 用y记录这个值
y = root;
// 如果之前x没有记录的话,用x记录前一个值
if (x == nullptr) {
x = pred;
}
else break;
}
pred = root;
root = root->right;
}
swap(x->val, y->val);
}
};- DFS
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (p == nullptr && q == nullptr) {
return true;
} else if (p == nullptr || q == nullptr) {
return false;
} else if (p->val != q->val) {
return false;
} else {
return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
}
};- BFS
异或^ :相同是0,不同是1
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (p == nullptr && q == nullptr) {
return true;
} else if (p == nullptr || q == nullptr) {
return false;
}
queue <TreeNode*> queue1, queue2;
queue1.push(p);
queue2.push(q);
while (!queue1.empty() && !queue2.empty()) {
auto node1 = queue1.front();
queue1.pop();
auto node2 = queue2.front();
queue2.pop();
if (node1->val != node2->val) {
return false;
}
auto left1 = node1->left, right1 = node1->right, left2 = node2->left, right2 = node2->right;
if ((left1 == nullptr) ^ (left2 == nullptr)) {
return false;
}
if ((right1 == nullptr) ^ (right2 == nullptr)) {
return false;
}
if (left1 != nullptr) {
queue1.push(left1);
}
if (right1 != nullptr) {
queue1.push(right1);
}
if (left2 != nullptr) {
queue2.push(left2);
}
if (right2 != nullptr) {
queue2.push(right2);
}
}
return queue1.empty() && queue2.empty();
}
};- DFS(递归)
class Solution {
public:
bool dfs(TreeNode* left, TreeNode* right) {
if (!left && !right) return true;
if (!left || !right) return false;
return left->val == right->val && dfs(left->left, right->right) && dfs(left->right, right->left);
}
bool isSymmetric(TreeNode* root) {
if (!root) return false;
return dfs(root, root);
}
};- BFS(迭代)
class Solution {
public:
bool check(TreeNode *u, TreeNode *v) {
queue <TreeNode*> q;
q.push(u); q.push(v);
while (!q.empty()) {
u = q.front(); q.pop();
v = q.front(); q.pop();
if (!u && !v) continue;
if ((!u || !v) || (u->val != v->val)) return false;
q.push(u->left);
q.push(v->right);
q.push(u->right);
q.push(v->left);
}
return true;
}
bool isSymmetric(TreeNode* root) {
return check(root, root);
}
};- DFS
class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == nullptr) return 0;
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
};- BFS
这种做法相对繁琐一些,需要遍历的时候在内层给一个循环控制输出完一层的结点后再进行下一次的大循环
class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == nullptr) return 0;
queue<TreeNode*> Q;
Q.push(root);
int ans = 0;
while (!Q.empty()) {
// 控制遍历一层的结点
int sz = Q.size();
while (sz > 0) {
TreeNode* node = Q.front();Q.pop();
if (node->left) Q.push(node->left);
if (node->right) Q.push(node->right);
sz -= 1;
}
ans += 1;
}
return ans;
}
};- DFS(自顶向下)
这里与上一题的方法相似,先求左右子树的深度,然后判断是否相差大于1,同时左右子树是否为平衡二叉树
class Solution {
public:
int height(TreeNode* root) {
if (root == NULL) {
return 0;
} else {
return max(height(root->left), height(root->right)) + 1;
}
}
bool isBalanced(TreeNode* root) {
if (root == NULL) {
return true;
} else {
return abs(height(root->left) - height(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
}
}
};- DFS(自底向上)
方法一由于是自顶向下递归,因此对于同一个节点,函数 height 会被重复调用,导致时间复杂度较高。如果使用自底向上的做法,则对于每个节点,函数 height 只会被调用一次。
自底向上递归的做法类似于后序遍历,对于当前遍历到的节点,先递归地判断其左右子树是否平衡,再判断以当前节点为根的子树是否平衡。如果一棵子树是平衡的,则返回其高度(高度一定是非负整数),否则返回−1。如果存在一棵子树不平衡,则整个二叉树一定不平衡。
class Solution {
public:
int height(TreeNode* root) {
if (root == NULL) {
return 0;
}
int leftHeight = height(root->left);
int rightHeight = height(root->right);
if (leftHeight == -1 || rightHeight == -1 || abs(leftHeight - rightHeight) > 1) {
return -1;
} else {
return max(leftHeight, rightHeight) + 1;
}
}
bool isBalanced(TreeNode* root) {
return height(root) >= 0;
}
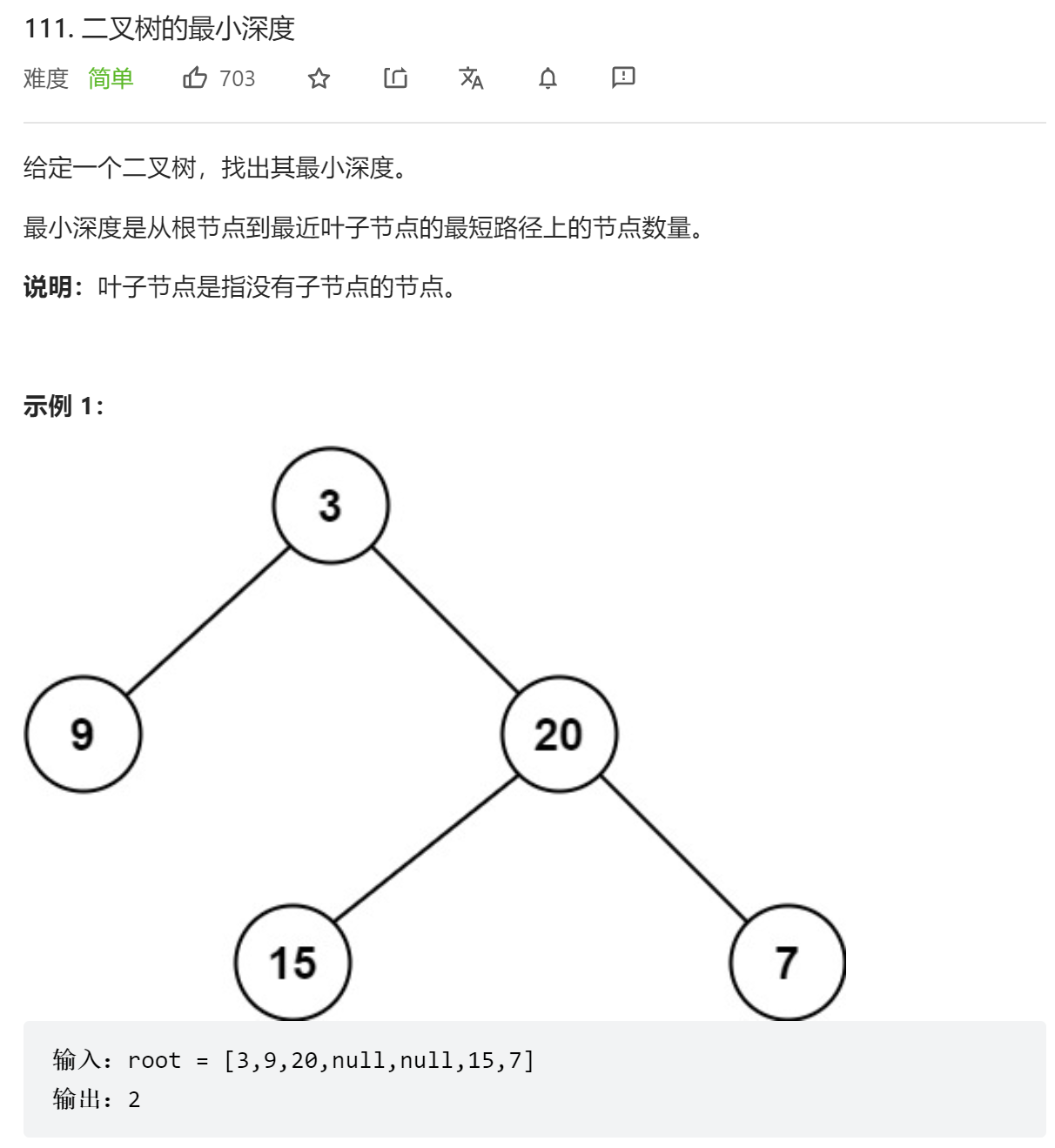
};- DFS
class Solution {
public:
int minDepth(TreeNode *root) {
if (root == nullptr) {
return 0;
}
// 当左右子树都为空时,最小深度为1
if (root->left == nullptr && root->right == nullptr) {
return 1;
}
// 最小深度为左右子树的最小深度的最小值 + 1
int min_depth = INT_MAX;
if (root->left != nullptr) {
min_depth = min(minDepth(root->left), min_depth);
}
if (root->right != nullptr) {
min_depth = min(minDepth(root->right), min_depth);
}
return min_depth + 1;
}
};- BFS
class Solution {
public:
int minDepth(TreeNode *root) {
if (root == nullptr) {
return 0;
}
queue<pair<TreeNode *, int> > que;
que.emplace(root, 1);
while (!que.empty()) {
TreeNode *node = que.front().first;
int depth = que.front().second;
que.pop();
if (node->left == nullptr && node->right == nullptr) {
return depth;
}
if (node->left != nullptr) {
que.emplace(node->left, depth + 1);
}
if (node->right != nullptr) {
que.emplace(node->right, depth + 1);
}
}
return 0;
}
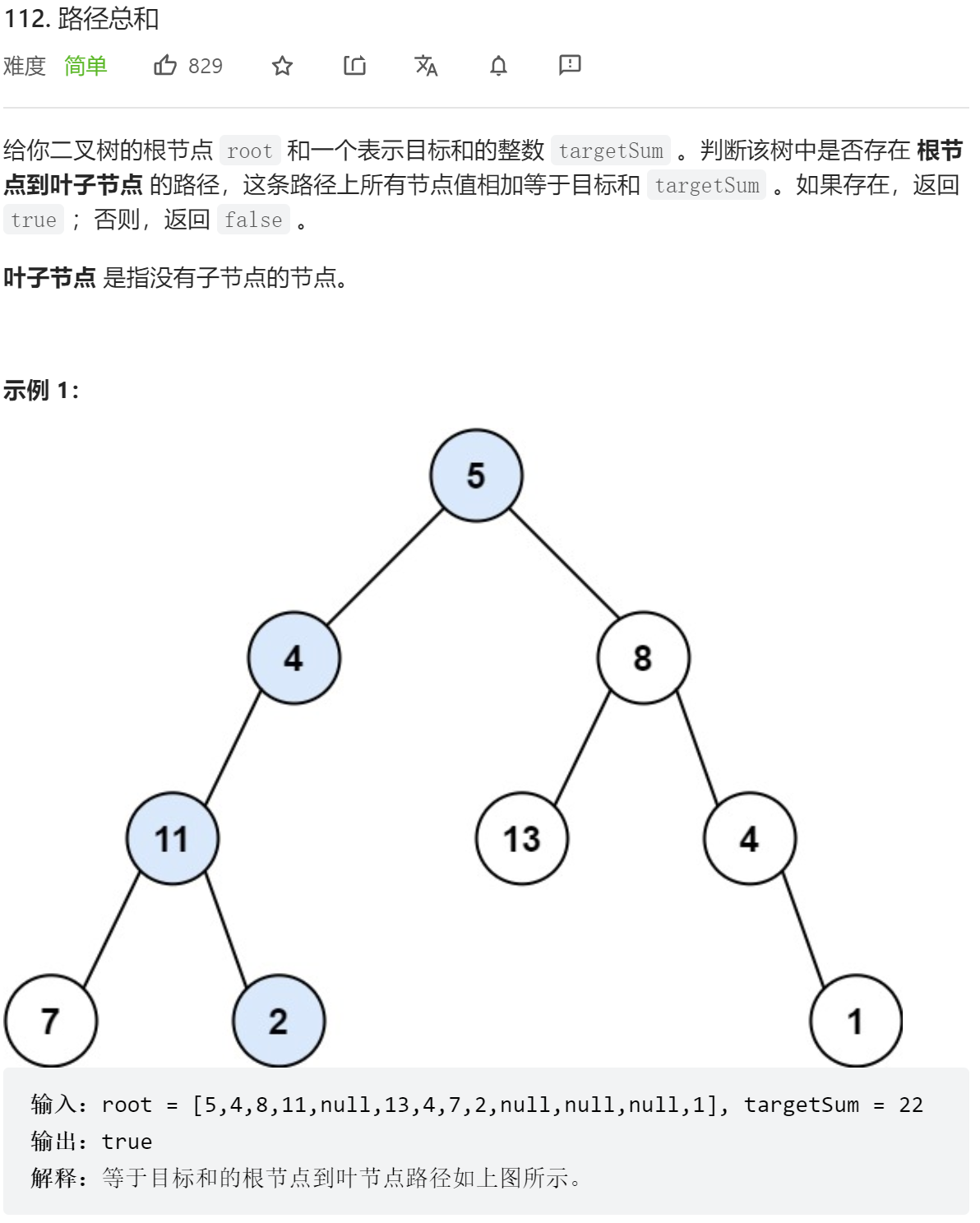
};- DFS
class Solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
if (!root) {
return false;
}
// 为叶子节点且路径和为sum时
if (!(root->left || root->right) && (root->val == sum)) {
return true;
}
// 否则要找左孩子或右孩子节点以下是否有存在和为sum-root->val的路径
else {
return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
}
}
};- BFS
广度优先搜索比较繁琐一点,需要两个队列,一个记录遍历的结点,一个记录该节点的路径和
class Solution {
public:
bool hasPathSum(TreeNode *root, int sum) {
if (root == nullptr) {
return false;
}
queue<TreeNode *> que_node;
queue<int> que_val;
que_node.push(root);
que_val.push(root->val);
while (!que_node.empty()) {
TreeNode *now = que_node.front();
int temp = que_val.front();
que_node.pop();
que_val.pop();
if (now->left == nullptr && now->right == nullptr) {
if (temp == sum) {
return true;
}
continue;
}
if (now->left != nullptr) {
que_node.push(now->left);
que_val.push(now->left->val + temp);
}
if (now->right != nullptr) {
que_node.push(now->right);
que_val.push(now->right->val + temp);
}
}
return false;
}
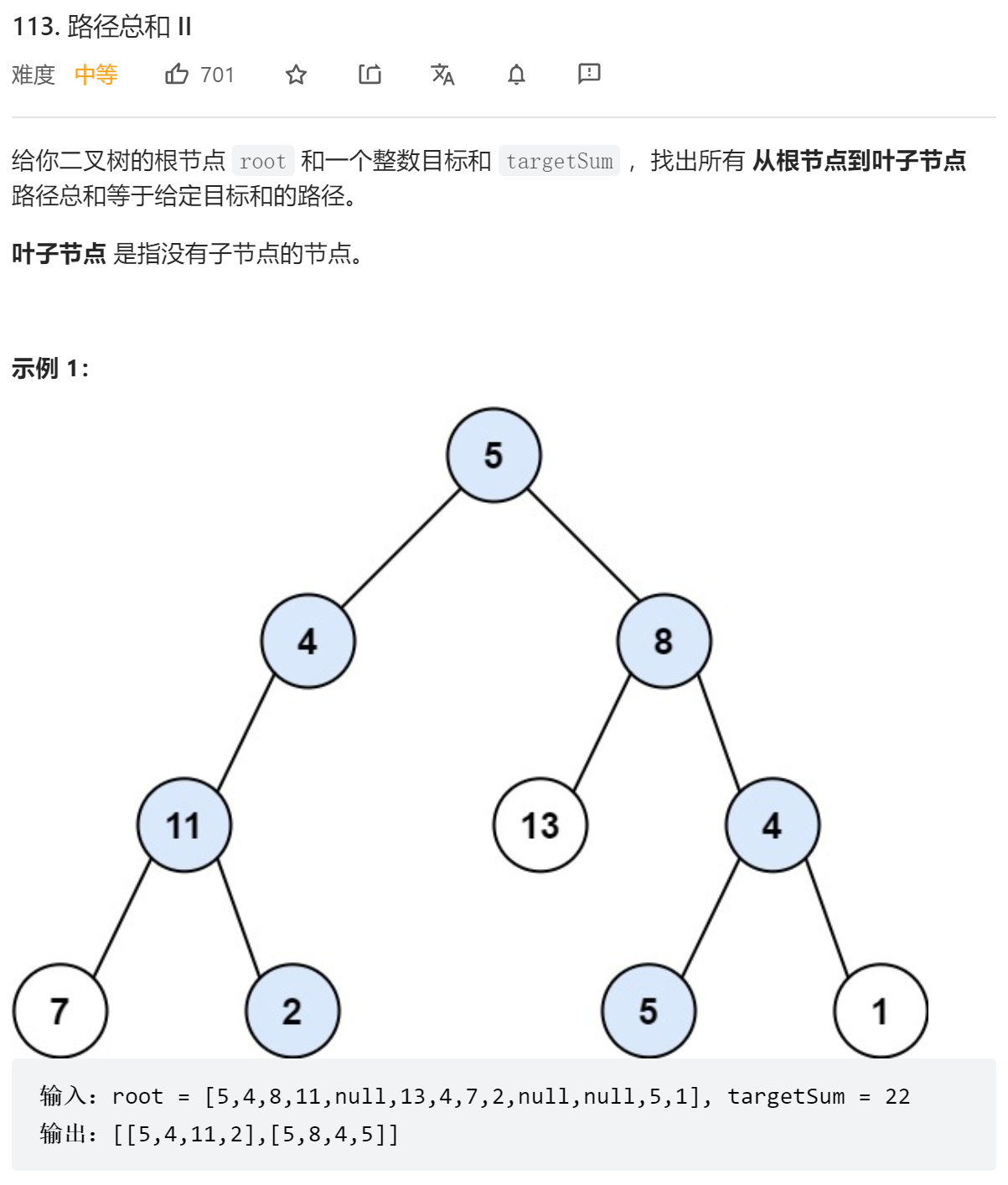
};上一题的进化版,其实难度差不多,同样可以用DFS和BFS做
- DFS
class Solution {
private:
vector<vector<int>> res;
public:
void dfs(TreeNode* root, int targetSum, vector<int> tmp) {
if (!root) return;
tmp.push_back(root->val);
if (!(root->left || root->right) && root->val == targetSum) {
res.push_back(tmp);
return;
}
dfs(root->left, targetSum - root->val, tmp);
dfs(root->right, targetSum - root->val, tmp);
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
vector<int> tmp;
dfs(root, targetSum, tmp);
return res;
}
};- BFS
BFS更繁琐了,还需要用一个哈希表去记录父节点,然后得到整体的路径,不建议用BFS做
class Solution {
public:
vector<vector<int>> ret;
// 记录父节点
unordered_map<TreeNode*, TreeNode*> parent;
// 不断往上得到父节点,最后反转得到路径
void getPath(TreeNode* node) {
vector<int> tmp;
while (node != nullptr) {
tmp.emplace_back(node->val);
node = parent[node];
}
reverse(tmp.begin(), tmp.end());
ret.emplace_back(tmp);
}
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
if (root == nullptr) {
return ret;
}
// BFS遍历所用的队列
queue<TreeNode*> que_node;
// 记录对应遍历位置的路径和
queue<int> que_sum;
que_node.emplace(root);
que_sum.emplace(0);
while (!que_node.empty()) {
TreeNode* node = que_node.front();
que_node.pop();
int rec = que_sum.front() + node->val;
que_sum.pop();
if (node->left == nullptr && node->right == nullptr) {
if (rec == targetSum) {
getPath(node);
}
} else {
if (node->left != nullptr) {
// 更新父节点的字典
parent[node->left] = node;
que_node.emplace(node->left);
que_sum.emplace(rec);
}
if (node->right != nullptr) {
// 更新父节点的字典
parent[node->right] = node;
que_node.emplace(node->right);
que_sum.emplace(rec);
}
}
}
return ret;
}
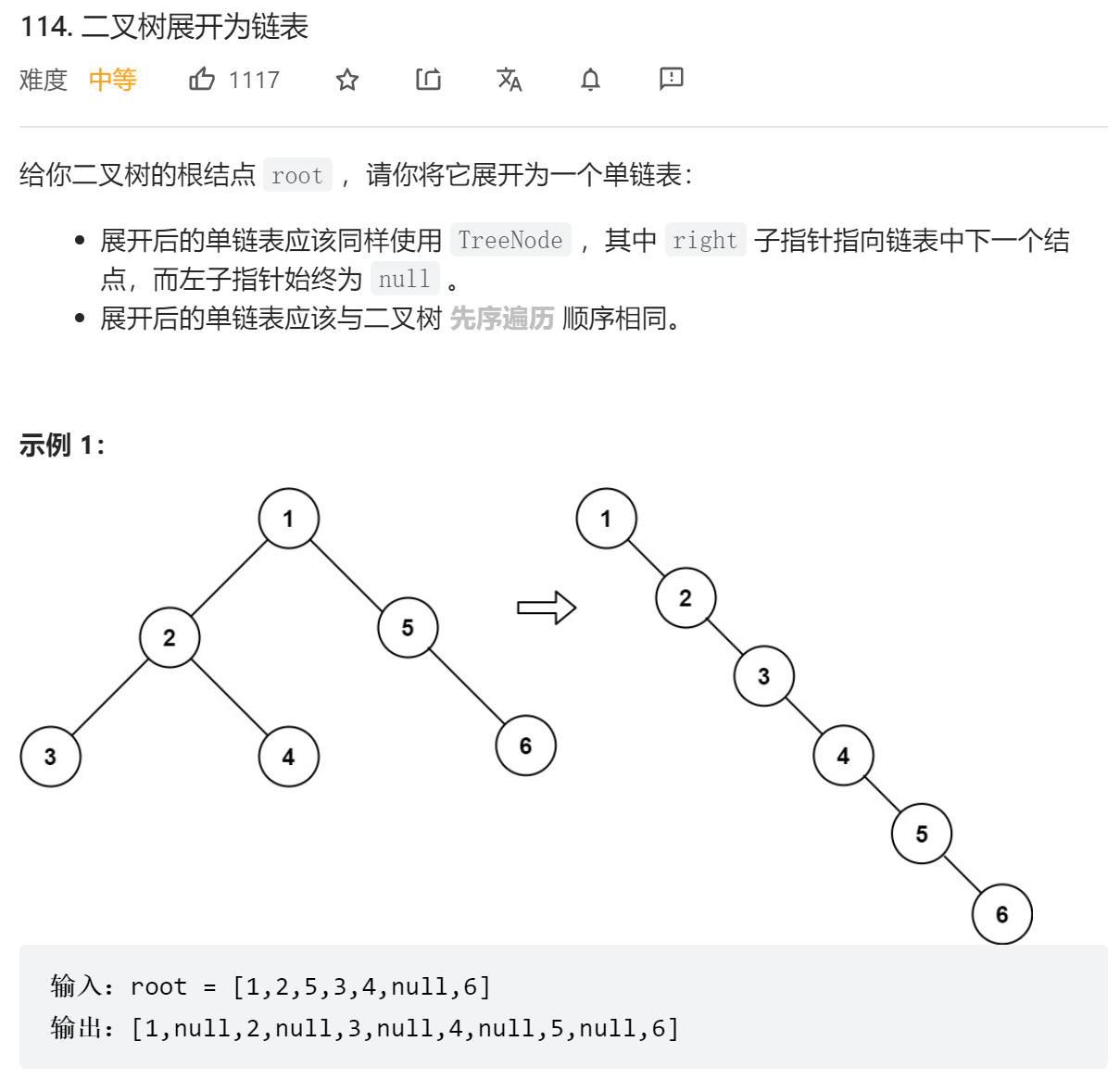
};这个思路很牛逼,建议多看,相当于倒序的前序遍历,这样就能得到前序遍历的后一个节点,然后让当前节点去指向他。
class Solution {
public:
TreeNode* last = nullptr;
void flatten(TreeNode* root) {
if (root == nullptr) return;
flatten(root->right);
flatten(root->left);
root->right = last;
root->left = nullptr;
last = root;
}
};或者采用更容易理解的前序遍历+构造的形式去做
class Solution {
public:
void flatten(TreeNode* root) {
vector<TreeNode*> l;
preorderTraversal(root, l);
int n = l.size();
for (int i = 1; i < n; i++) {
TreeNode *prev = l.at(i - 1), *curr = l.at(i);
prev->left = nullptr;
prev->right = curr;
}
}
void preorderTraversal(TreeNode* root, vector<TreeNode*> &l) {
if (root != NULL) {
l.push_back(root);
preorderTraversal(root->left, l);
preorderTraversal(root->right, l);
}
}
};- 用BFS可以很简单地做出来
class Solution {
public:
Node* connect(Node* root) {
if (!root) return root;
queue<Node*> q;
q.push(root);
while (!q.empty()) {
int size = q.size();
for (int i = 0; i < size; i++) {
Node* tmp = q.front();
q.pop();
tmp->next = (i == size-1)? NULL: q.front();
if (tmp->left)
q.push(tmp->left);
if (tmp->right)
q.push(tmp->right);
}
}
return root;
}
};- 如果面试官变态,要你用O(1)空间做,就把下面的代码呼他脸上
class Solution {
public:
Node* connect(Node* root) {
if (root == nullptr) {
return root;
}
// 从根节点开始
Node* leftmost = root;
while (leftmost->left != nullptr) {
// 遍历这一层节点组织成的链表,为下一层的节点更新 next 指针
Node* head = leftmost;
while (head != nullptr) {
// CONNECTION 1
head->left->next = head->right;
// CONNECTION 2
if (head->next != nullptr) {
head->right->next = head->next->left;
}
// 指针向后移动
head = head->next;
}
// 去下一层的最左的节点
leftmost = leftmost->left;
}
return root;
}
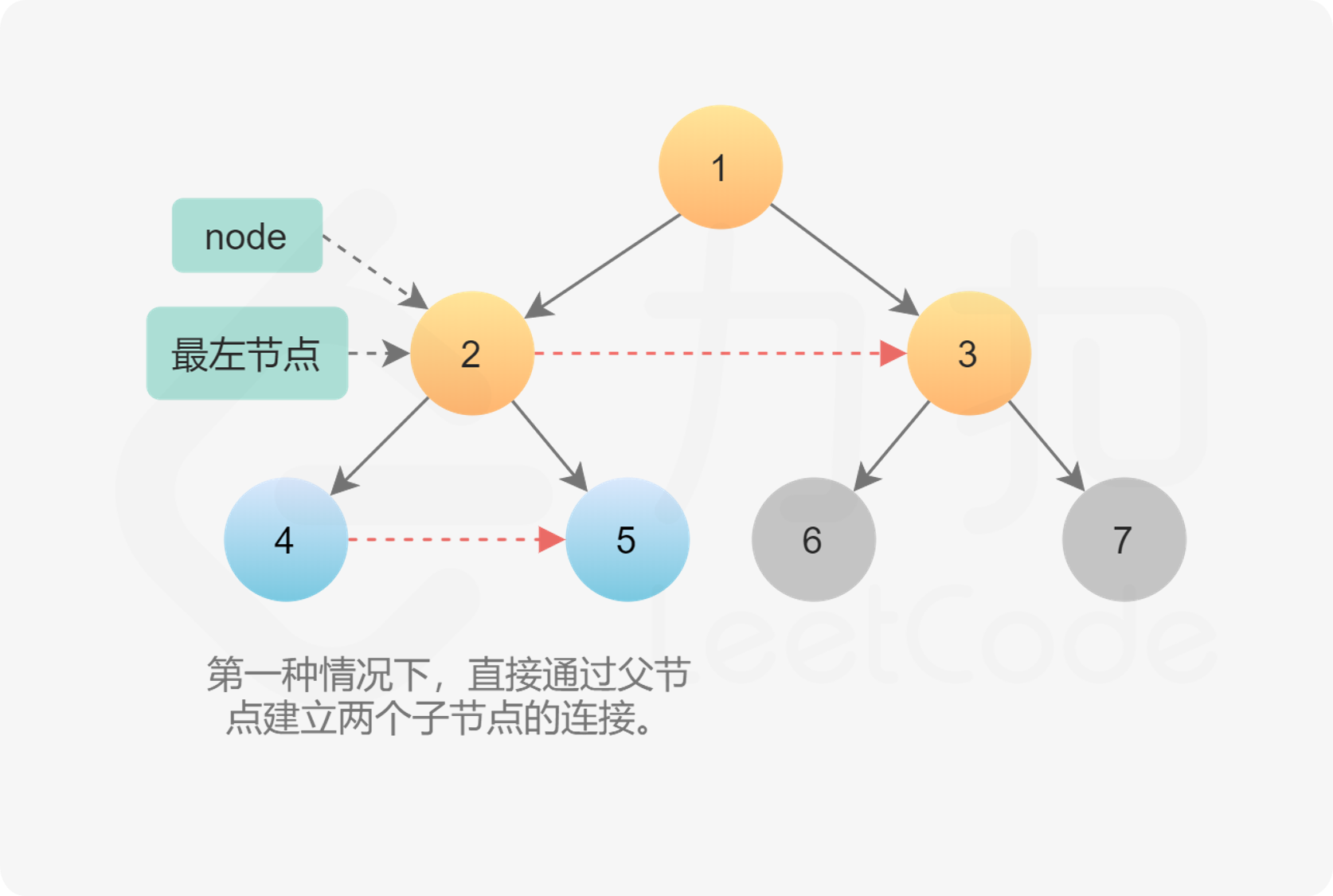
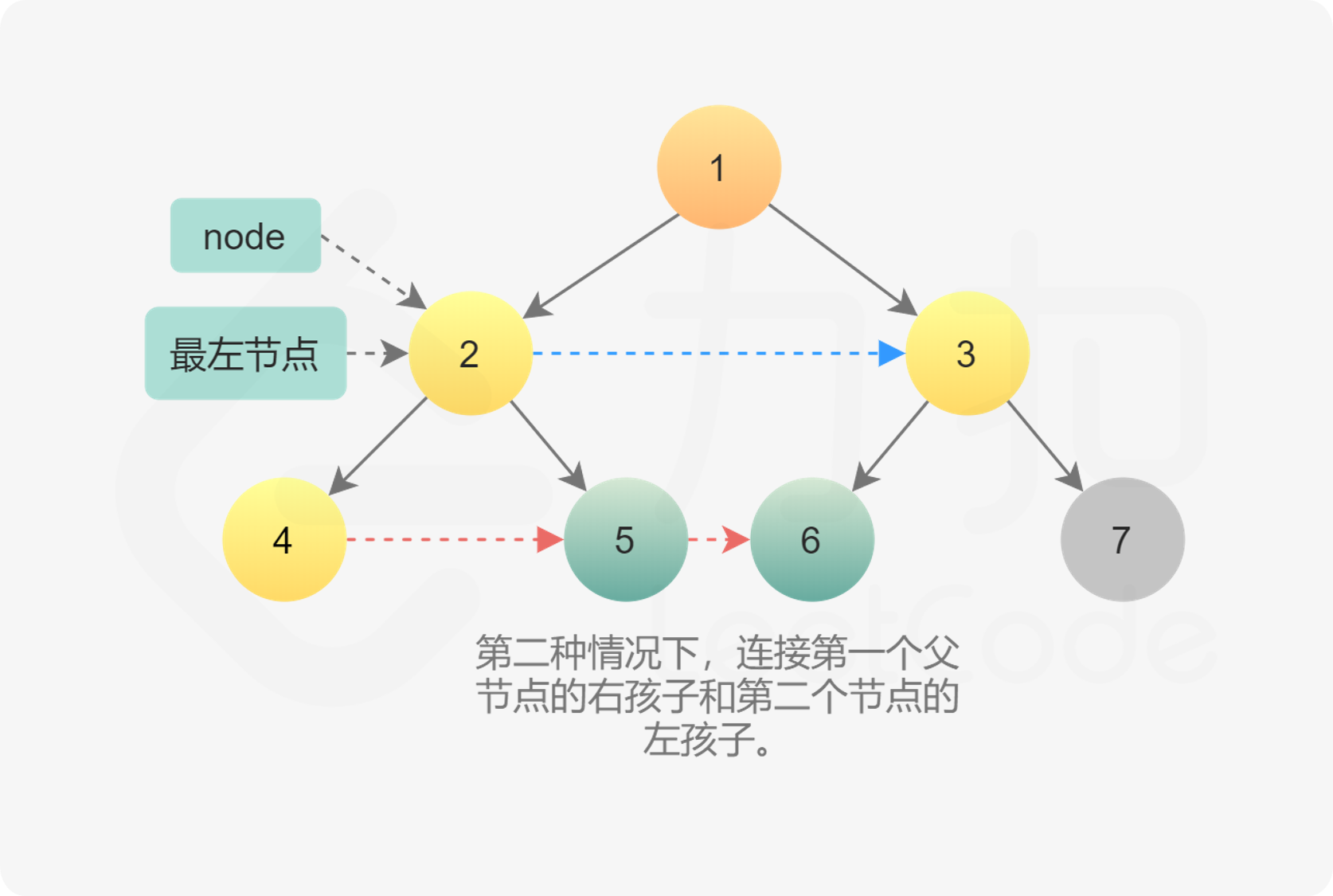
};刚说完变态,变态就来了,要求用O(1)做,且不是完美二叉树,换言之,就是不一定每个节点都有左右孩子。
代码跟上一题基本一样,唯一不同就是需要一个变量去记录下一层起始点,因为不一定是最左边的做孩子了(不一定有左孩子)
class Solution {
public:
void handle(Node* &last, Node* &p, Node* &nextStart) {
if (last) {
last->next = p;
}
// 记录第一个连接的节点
if (!nextStart) {
nextStart = p;
}
last = p;
}
Node* connect(Node* root) {
if (!root) {
return nullptr;
}
Node *start = root;
while (start) {
Node *last = nullptr, *nextStart = nullptr;
for (Node *p = start; p != nullptr; p = p->next) {
if (p->left) {
handle(last, p->left, nextStart);
}
if (p->right) {
handle(last, p->right, nextStart);
}
}
start = nextStart;
}
return root;
}
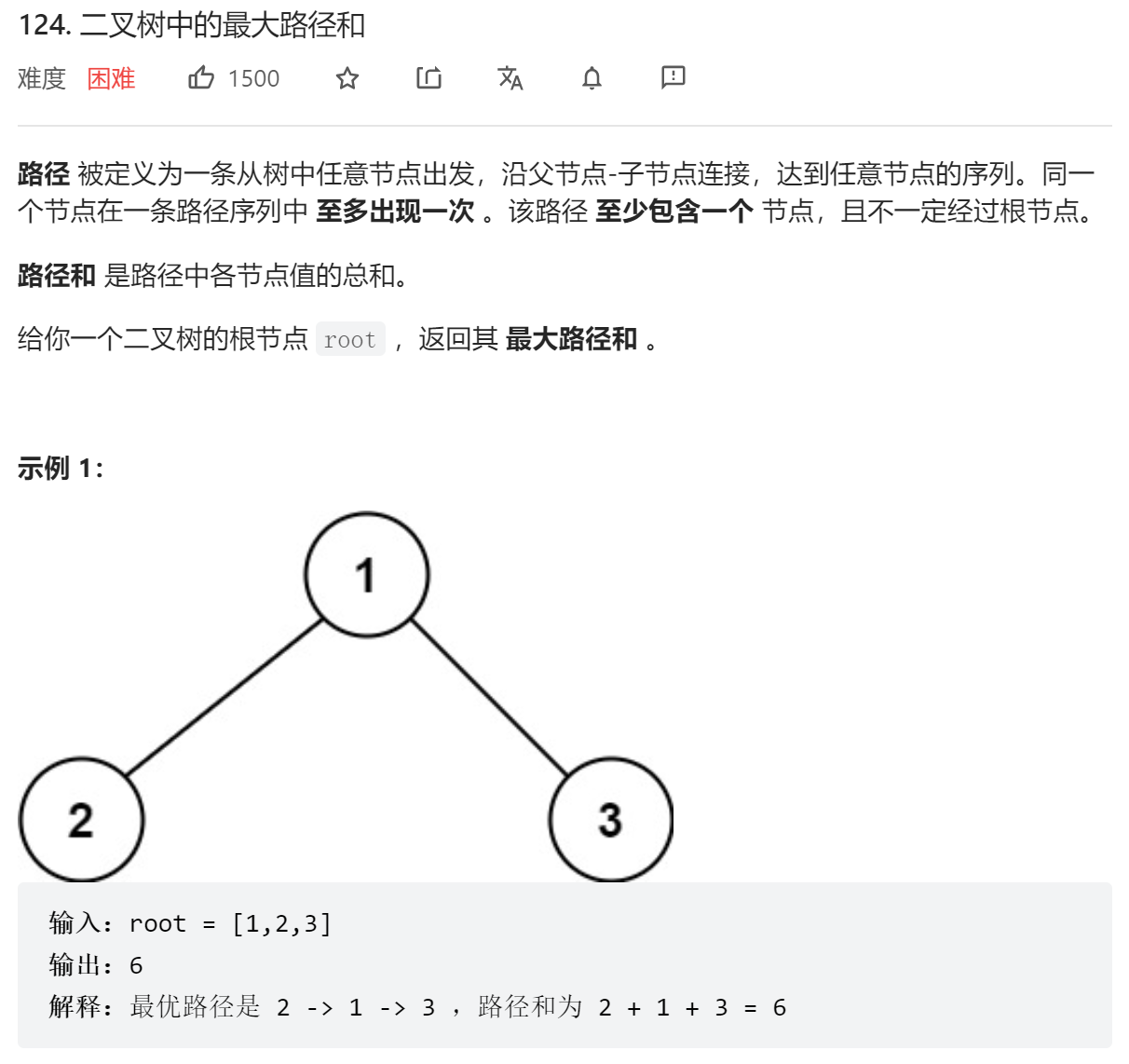
};DFS递归做法,分别求两边的路径和(当计算出负数时置为0),最大路径和为左路径和+右路径和+当前节点值
class Solution {
private:
int res = INT_MIN;
public:
// 以root为起始点的最大路径和
int dfs(TreeNode* root) {
if (!root) return 0;
int left = max(dfs(root->left), 0);
int right = max(dfs(root->right), 0);
res = max(res, left + right + root->val);
// 因为root为起点,最终只取大的一边的路径和
return max(left, right) + root->val;
}
int maxPathSum(TreeNode* root) {
dfs(root);
return res;
}
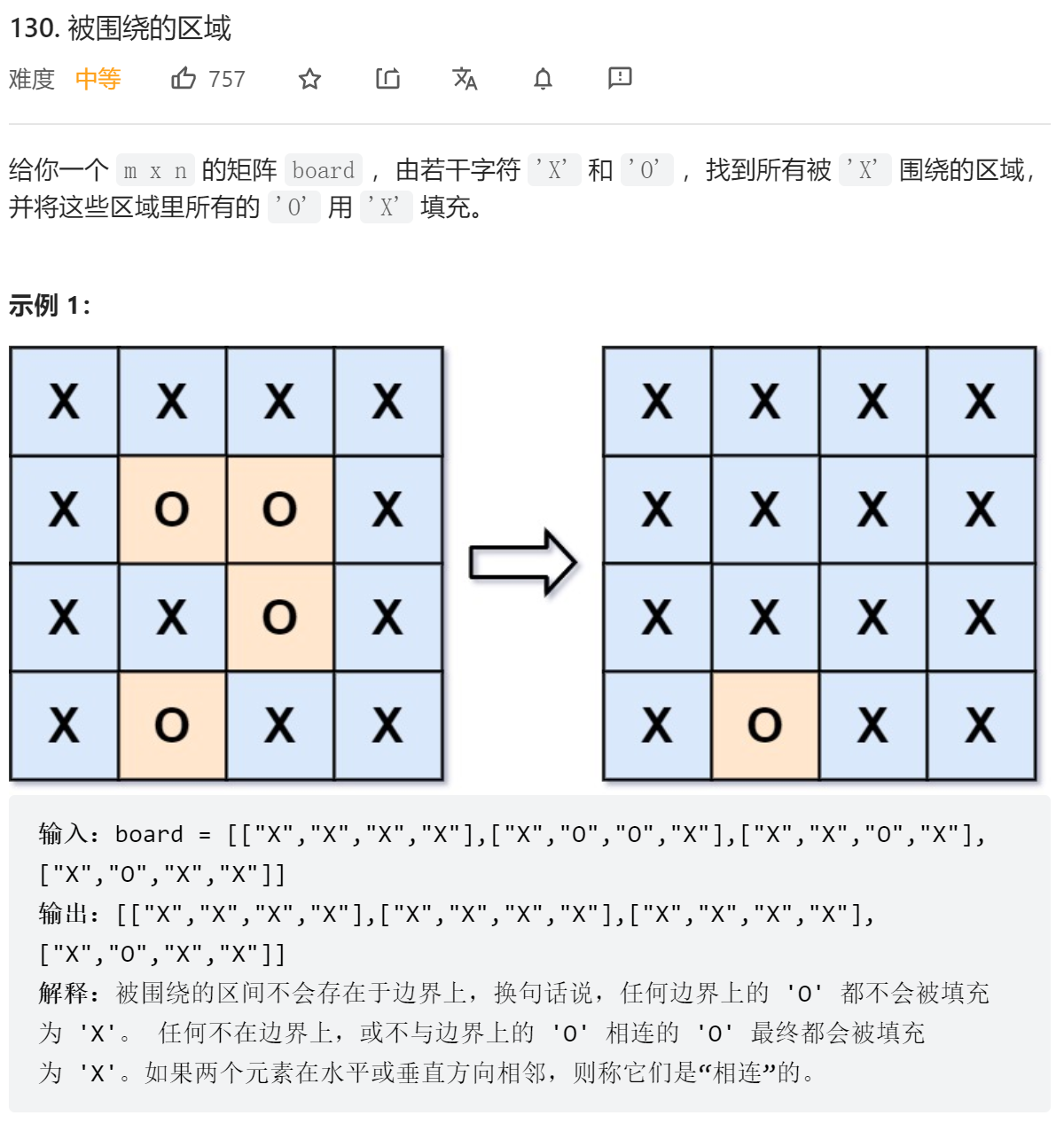
};把标记过的字母 O 修改为字母 A
- DFS
class Solution {
public:
int n, m;
void dfs(vector<vector<char>>& board, int x, int y) {
if (x < 0 || x >= n || y < 0 || y >= m || board[x][y] != 'O') {
return;
}
board[x][y] = 'A';
dfs(board, x + 1, y);
dfs(board, x - 1, y);
dfs(board, x, y + 1);
dfs(board, x, y - 1);
}
void solve(vector<vector<char>>& board) {
n = board.size();
if (n == 0) {
return;
}
m = board[0].size();
// 外围的O全都遍历
for (int i = 0; i < n; i++) {
dfs(board, i, 0);
dfs(board, i, m - 1);
}
// 外围的O全都遍历
for (int i = 1; i < m - 1; i++) {
dfs(board, 0, i);
dfs(board, n - 1, i);
}
// 遍历过的A设回O
// 没遍历到的O改成X,说明是被包围住的O
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'A') {
board[i][j] = 'O';
} else if (board[i][j] == 'O') {
board[i][j] = 'X';
}
}
}
}
};- BFS
class Solution {
public:
const int dx[4] = {1, -1, 0, 0};
const int dy[4] = {0, 0, 1, -1};
void solve(vector<vector<char>>& board) {
int n = board.size();
if (n == 0) {
return;
}
int m = board[0].size();
queue<pair<int, int>> que;
// 外围的O都遍历(入队)
for (int i = 0; i < n; i++) {
if (board[i][0] == 'O') {
que.emplace(i, 0);
board[i][0] = 'A';
}
if (board[i][m - 1] == 'O') {
que.emplace(i, m - 1);
board[i][m - 1] = 'A';
}
}
for (int i = 1; i < m - 1; i++) {
if (board[0][i] == 'O') {
que.emplace(0, i);
board[0][i] = 'A';
}
if (board[n - 1][i] == 'O') {
que.emplace(n - 1, i);
board[n - 1][i] = 'A';
}
}
while (!que.empty()) {
int x = que.front().first, y = que.front().second;
que.pop();
// 向上下左右四个方向遍历
for (int i = 0; i < 4; i++) {
int mx = x + dx[i], my = y + dy[i];
if (mx < 0 || my < 0 || mx >= n || my >= m || board[mx][my] != 'O') {
continue;
}
que.emplace(mx, my);
board[mx][my] = 'A';
}
}
// 遍历过的A设回O
// 没遍历到的O改成X,说明是被包围住的O
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'A') {
board[i][j] = 'O';
} else if (board[i][j] == 'O') {
board[i][j] = 'X';
}
}
}
}
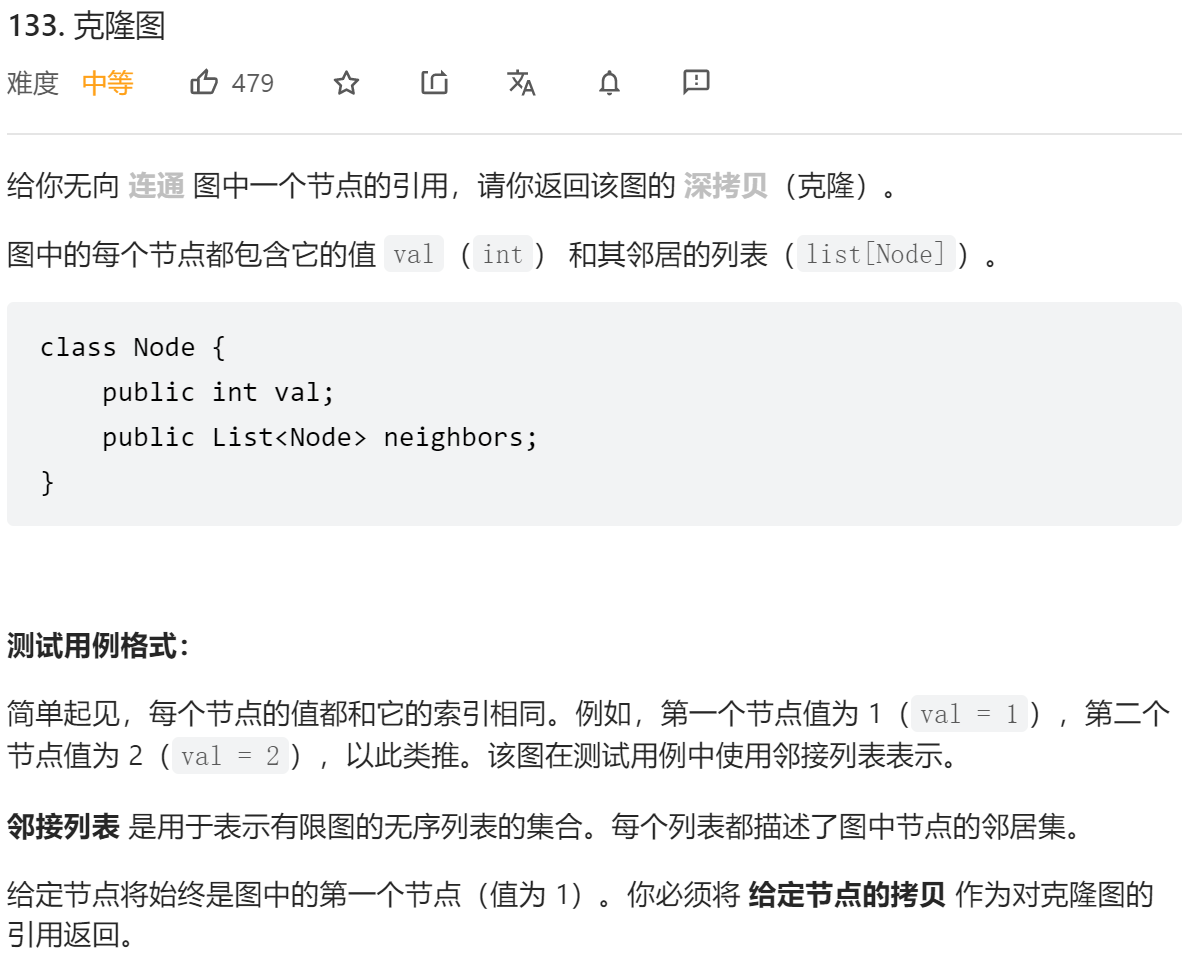
};一边遍历要一边构造新的节点,两种方法都需要借助哈希表记录被克隆过的节点来避免陷入死循环
- DFS
class Solution {
public:
unordered_map<Node*, Node*> visited;
Node* cloneGraph(Node* node) {
if (node == nullptr) {
return node;
}
// 如果该节点已经被访问过了,则直接从哈希表中取出对应的克隆节点返回
if (visited.find(node) != visited.end()) {
return visited[node];
}
// 克隆节点,注意到为了深拷贝我们不会克隆它的邻居的列表
Node* cloneNode = new Node(node->val);
// 哈希表存储
visited[node] = cloneNode;
// 遍历该节点的邻居并更新克隆节点的邻居列表
for (auto& neighbor: node->neighbors) {
cloneNode->neighbors.emplace_back(cloneGraph(neighbor));
}
return cloneNode;
}
};- BFS
class Solution {
public:
Node* cloneGraph(Node* node) {
if (node == nullptr) {
return node;
}
unordered_map<Node*, Node*> visited;
// 将题目给定的节点添加到队列
queue<Node*> Q;
Q.push(node);
// 克隆第一个节点并存储到哈希表中
visited[node] = new Node(node->val);
// 广度优先搜索
while (!Q.empty()) {
// 取出队列的头节点
auto n = Q.front();
Q.pop();
// 遍历该节点的邻居
for (auto& neighbor: n->neighbors) {
if (visited.find(neighbor) == visited.end()) {
// 如果没有被访问过,就克隆并存储在哈希表中
visited[neighbor] = new Node(neighbor->val);
// 将邻居节点加入队列中
Q.push(neighbor);
}
// 更新当前节点的邻居列表
visited[n]->neighbors.emplace_back(visited[neighbor]);
}
}
return visited[node];
}
};/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<string> res;
vector<string> binaryTreePaths(TreeNode* root) {
string tmp = "";
dfs(root, tmp);
return res;
}
void dfs(TreeNode* root, string tmp) {
if (!root) return;
tmp += to_string(root->val) + "->";
if (!(root->left || root->right)) {
tmp.pop_back();
tmp.pop_back();
res.emplace_back(tmp);
return;
}
dfs(root->left, tmp);
dfs(root->right, tmp);
}
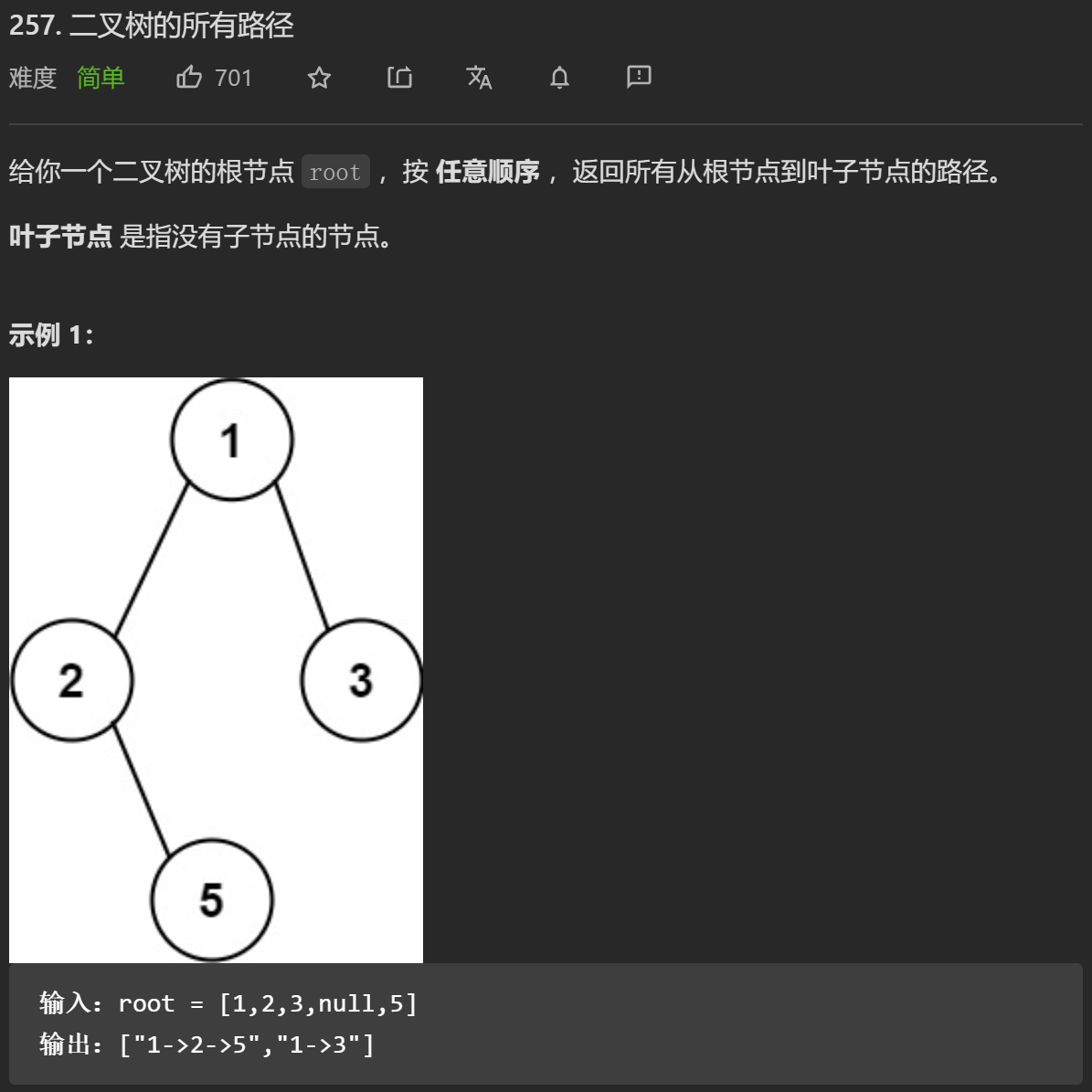
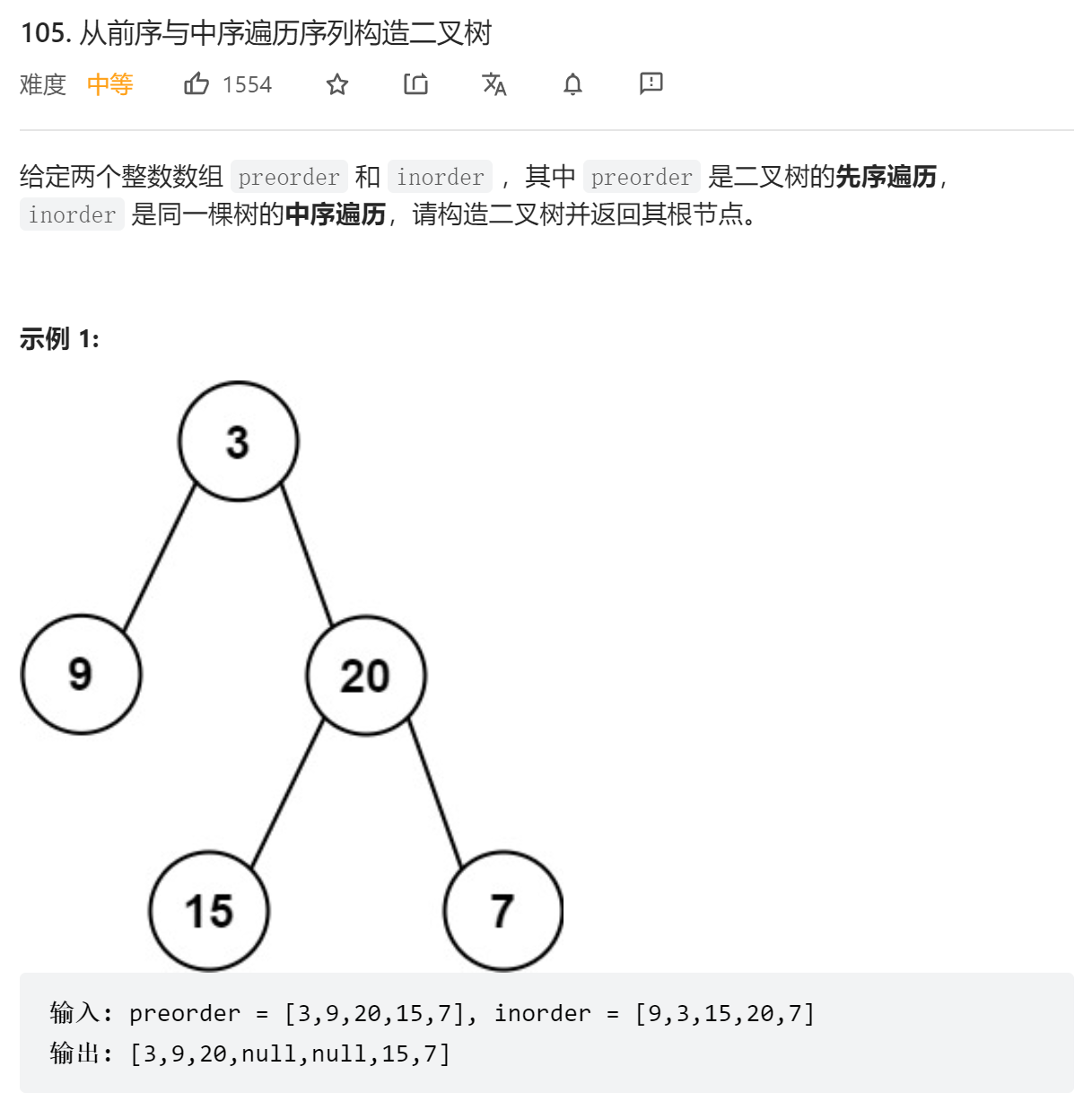
};从前序与中序遍历序列构造二叉树
递归地构建左子树和右子树,求出这两个子树在前序和中序中的位置区间
class Solution {
private:
unordered_map<int, int> index;
public:
TreeNode* myBuildTree(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
if (preorder_left > preorder_right) {
return nullptr;
}
// 前序遍历中的第一个节点就是根节点
int preorder_root = preorder_left;
// 在中序遍历中定位根节点
int inorder_root = index[preorder[preorder_root]];
// 先把根节点建立出来
TreeNode* root = new TreeNode(preorder[preorder_root]);
// 得到左子树中的节点数目
int size_left_subtree = inorder_root - inorder_left;
// 递归地构造左子树,并连接到根节点
// 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
// 递归地构造右子树,并连接到根节点
// 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = preorder.size();
// 构造哈希映射,帮助我们快速定位根节点
for (int i = 0; i < n; ++i) {
index[inorder[i]] = i;
}
return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
}
};从中序与后序序列构造二叉树
这题跟那上面一样,注意后序序列的区间计算
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
unordered_map<int, int> index;
public:
TreeNode* myBuildTree(const vector<int>& inorder, const vector<int>& postorder, int inorder_left, int inorder_right, int postorder_left, int postorder_right) {
if (inorder_left > inorder_right) {
return nullptr;
}
// 后序遍历中的最后一个节点就是根节点
int postorder_root = postorder_right;
// 在中序遍历中定位根节点
int inorder_root = index[postorder[postorder_root]];
// 先把根节点建立出来
TreeNode* root = new TreeNode(postorder[postorder_root]);
// 得到右子树中的节点数目
int size_right_subtree = inorder_right - inorder_root;
// 递归地构造左子树,并连接到根节点
root->left = myBuildTree(inorder, postorder, inorder_left, inorder_root - 1, postorder_left, postorder_right - size_right_subtree - 1);
// 递归地构造右子树,并连接到根节点
root->right = myBuildTree(inorder, postorder, inorder_root + 1, inorder_right, postorder_right - size_right_subtree + 1, postorder_right - 1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
int n = inorder.size();
// 构造哈希映射,帮助我们快速定位根节点
for (int i = 0; i < n; ++i) {
index[inorder[i]] = i;
}
return myBuildTree(inorder, postorder, 0, n - 1, 0, n - 1);
}
};输出拓扑排序的方法如链接所示,可点击查看原理
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
// 记录边
vector<vector<int>> edges(numCourses);
// 记录入度
vector<int> incount(numCourses);
// 统计边和入度
for (auto& p: prerequisites) {
edges[p[1]].push_back(p[0]);
incount[p[0]]++;
}
// 广度优先搜索
queue<int> q;
vector<int> res;
int visit = 0;
// 入度为0则入队
for (int i = 0; i < numCourses; i++) {
if (incount[i] == 0) {
q.push(i);
}
}
// 将栈内的节点出栈,则表明访问过了,visit加一
// 出栈的同时要将该节点的有向边的节点入度减一
// 最终的结果如果访问的节点数不等于总个数,则表明有环
while (!q.empty()) {
int cur = q.front();
res.push_back(cur);
q.pop();
visit++;
for (auto& t: edges[cur]) {
incount[t]--;
if (incount[t] == 0) {
q.push(t);
}
}
}
return (visit == numCourses)? res: vector<int>();
}
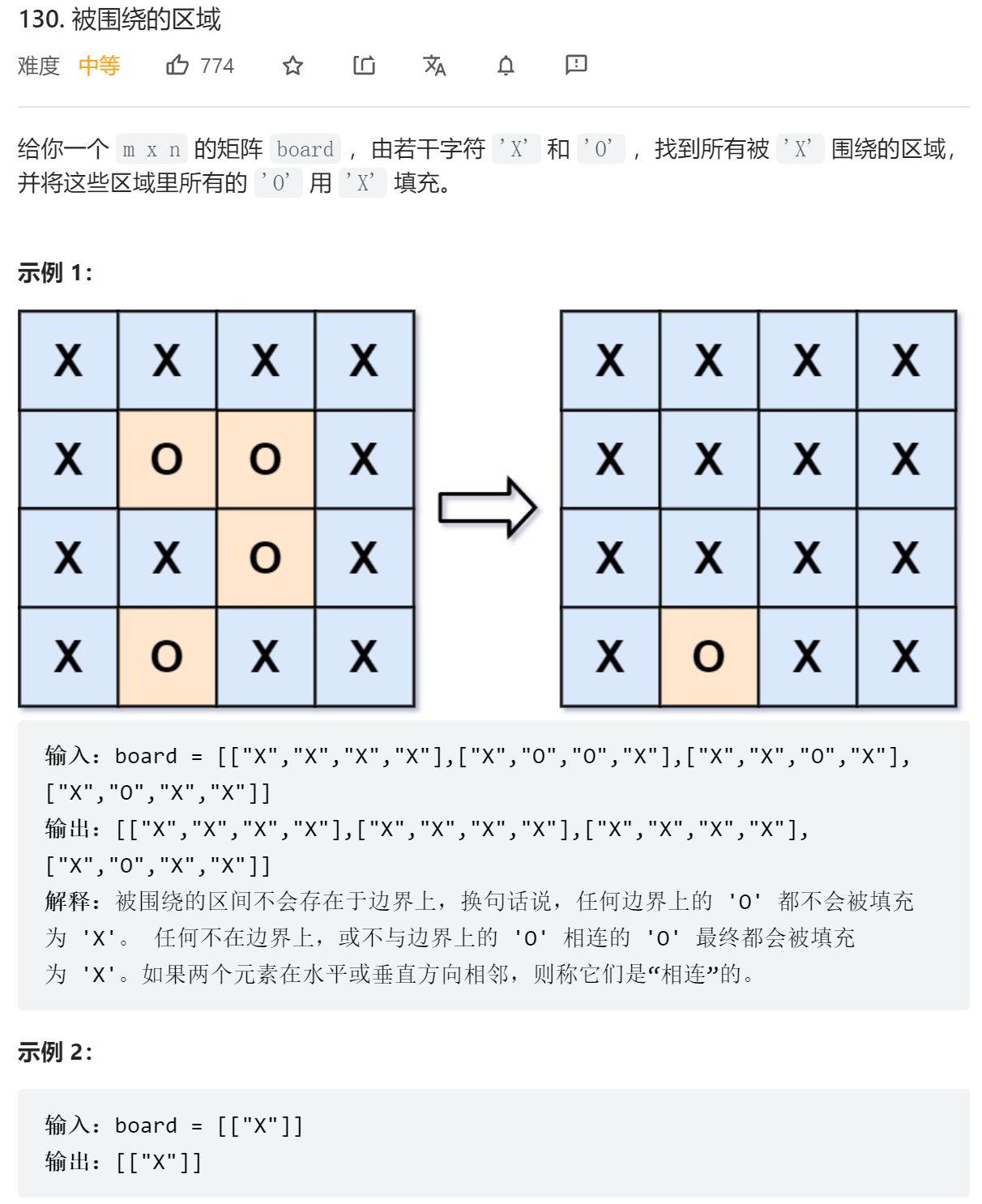
};从外围开始广度优先遍历,遍历到的都不可能是被围绕的区域,把这些区域填成另外的A,遍历完后把A还原成O,把O变成X
class Solution {
public:
const int dx[4] = {1, -1, 0, 0};
const int dy[4] = {0, 0, 1, -1};
void solve(vector<vector<char>>& board) {
int n = board.size();
if (n == 0) {
return;
}
int m = board[0].size();
queue<pair<int, int>> que;
// 矩阵外围四周为O的入队
for (int i = 0; i < n; i++) {
if (board[i][0] == 'O') {
que.emplace(i, 0);
}
if (board[i][m - 1] == 'O') {
que.emplace(i, m - 1);
}
}
for (int i = 1; i < m - 1; i++) {
if (board[0][i] == 'O') {
que.emplace(0, i);
}
if (board[n - 1][i] == 'O') {
que.emplace(n - 1, i);
}
}
// 广度优先遍历
while (!que.empty()) {
int x = que.front().first, y = que.front().second;
que.pop();
board[x][y] = 'A';
for (int i = 0; i < 4; i++) {
int mx = x + dx[i], my = y + dy[i];
// 超出边界或者不为O则跳过
if (mx < 0 || my < 0 || mx >= n || my >= m || board[mx][my] != 'O') {
continue;
}
que.emplace(mx, my);
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'A') {
board[i][j] = 'O';
} else if (board[i][j] == 'O') {
board[i][j] = 'X';
}
}
}
}
};这里有个链接讲的非常好,很详细,但是构建next数组时有循环条件有点错误,需要注意一下
class Solution {
public:
int* buildNext(string s) {
int m = s.size();
int* next = new int[m];
next[0] = -1;
int i = 0, j = -1;
// 注意这里千万不能用i < m,因为先让i++ j++再next[i] = j,会导致越界
while (i < m - 1) {
if (j == -1 || s[i] == s[j]) {
i++;
j++;
next[i] = j;
}
else {
j = next[j];
}
}
return next;
}
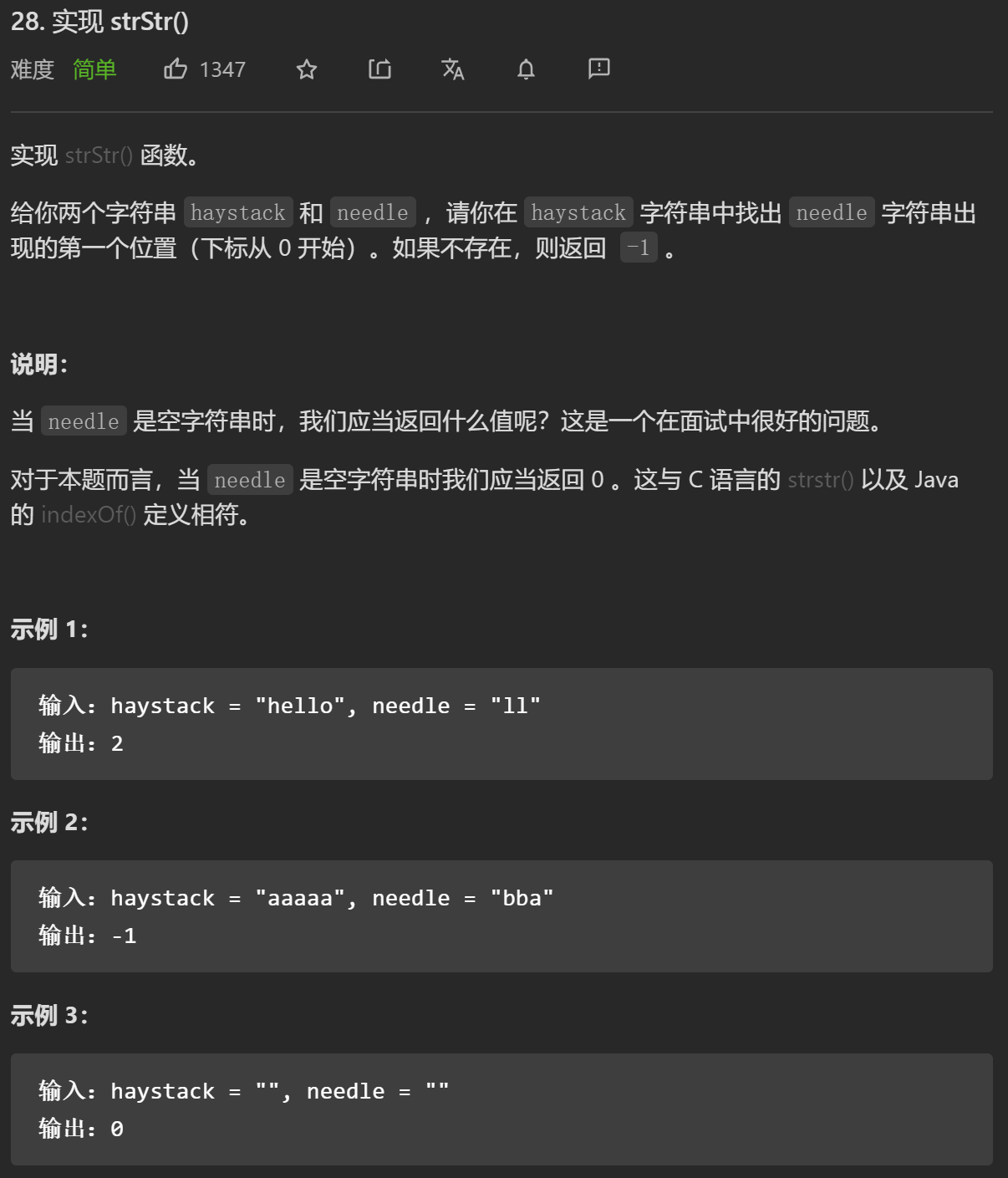
int strStr(string haystack, string needle) {
int n = haystack.size();
int m = needle.size();
if (m == 0) {
return 0;
}
int i = 0, j = 0;
int* next = buildNext(needle);
while (i < n && j < m) {
if (j == -1 || haystack[i] == needle[j]) {
i++;
j++;
}
else {
j = next[j];
}
}
if (j == m) {
return i - j;
}
return -1;
}
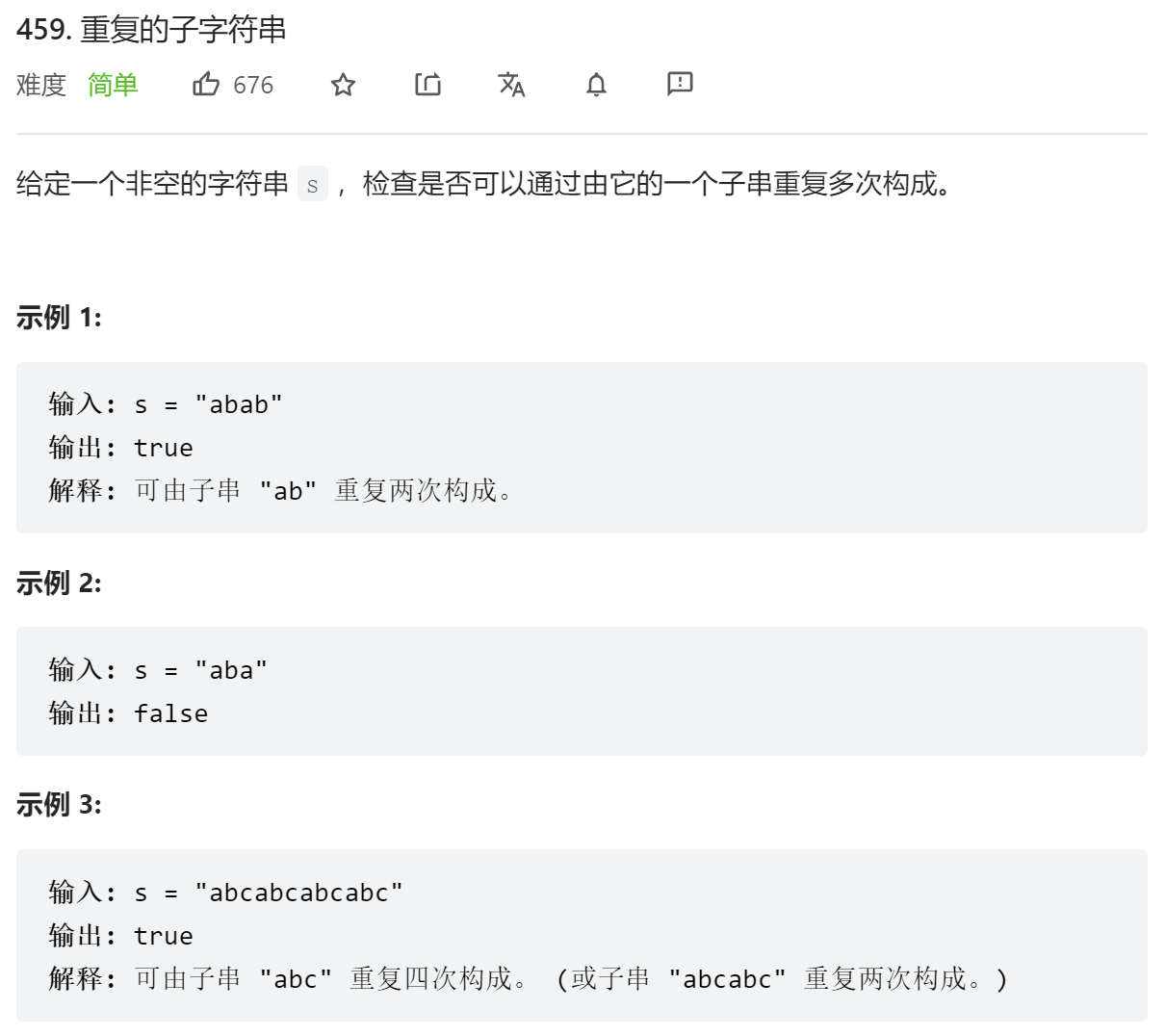
};如果S不包含重复的子字符串,则S本身就是所谓的“重复子字符串”(这里方便自己理解,视为重复一次,不深究= =),str = S+S,说明S是str的重复子字符串,刨去str首尾两个字符之后(相当于分别破坏前一个S头部和后一个S尾部),不能满足str包含S,如果str依旧包含S,说明S是重复子字符串构成的。
这里判断字符串中是否包含子串,可用kmp算法,也可用自带的c++函数
- 自带函数
class Solution {
public:
bool repeatedSubstringPattern(string s) {
// find第二个参数表示从第几号索引开始找
return (s + s).find(s, 1) != s.size();
}
};- kmp
class Solution {
public:
int* buildNext(string s) {
int n = s.length();
int* next = new int[n];
int i = 0, j = -1;
next[0] = -1;
while (i < n - 1) {
if (j == -1 || s[i] == s[j]) {
i++;
j++;
next[i] = j;
}
else {
j = next[j];
}
}
return next;
}
bool repeatedSubstringPattern(string s) {
string str = s + s;
int n = s.length();
int m = n + n - 2;
str = str.substr(1, m);
int* next = buildNext(s);
int i = 0, j = 0;
while (i < m && j < n) {
if (j == -1 || str[i] == s[j]) {
i++;
j++;
}
else {
j = next[j];
}
}
return j == n;
}
};class Solution {
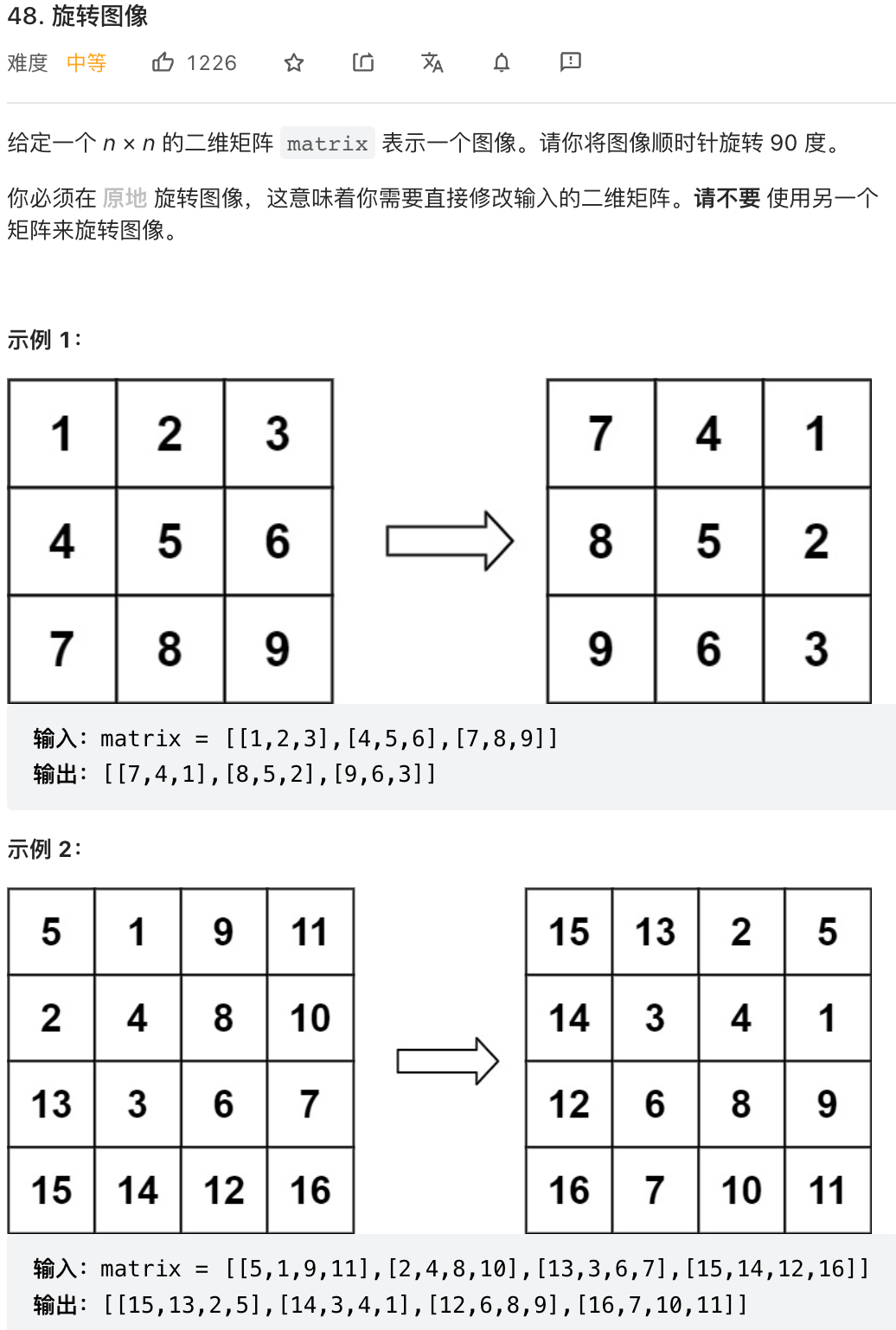
public:
void rotate(vector<vector<int>>& matrix) {
int n = matrix.size();
// 水平翻转
for (int i = 0; i < n / 2; ++i) {
for (int j = 0; j < n; ++j) {
swap(matrix[i][j], matrix[n - i - 1][j]);
}
}
// 主对角线翻转
for (int i = 0; i < n; ++i) {
for (int j = 0; j < i; ++j) {
swap(matrix[i][j], matrix[j][i]);
}
}
}
};- 直接模拟的写法
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<vector<int>> direct = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int m = matrix.size();
int n = matrix[0].size();
vector<vector<int>> visited(m, vector<int>(n));
vector<int> res;
int x = 0, y = 0, i = 0, count = 1;
res.push_back(matrix[x][y]);
visited[x][y] = 1;
while (count < m * n) {
int newx = x + direct[i % 4][0];
int newy = y + direct[i % 4][1];
if (newx >= m || newx < 0 || newy >= n || newy < 0 || visited[newx][newy]) {
i++;
continue;
}
else {
visited[newx][newy] = 1;
res.push_back(matrix[newx][newy]);
count++;
x = newx;
y = newy;
}
}
return res;
}
};- 按层模拟的写法
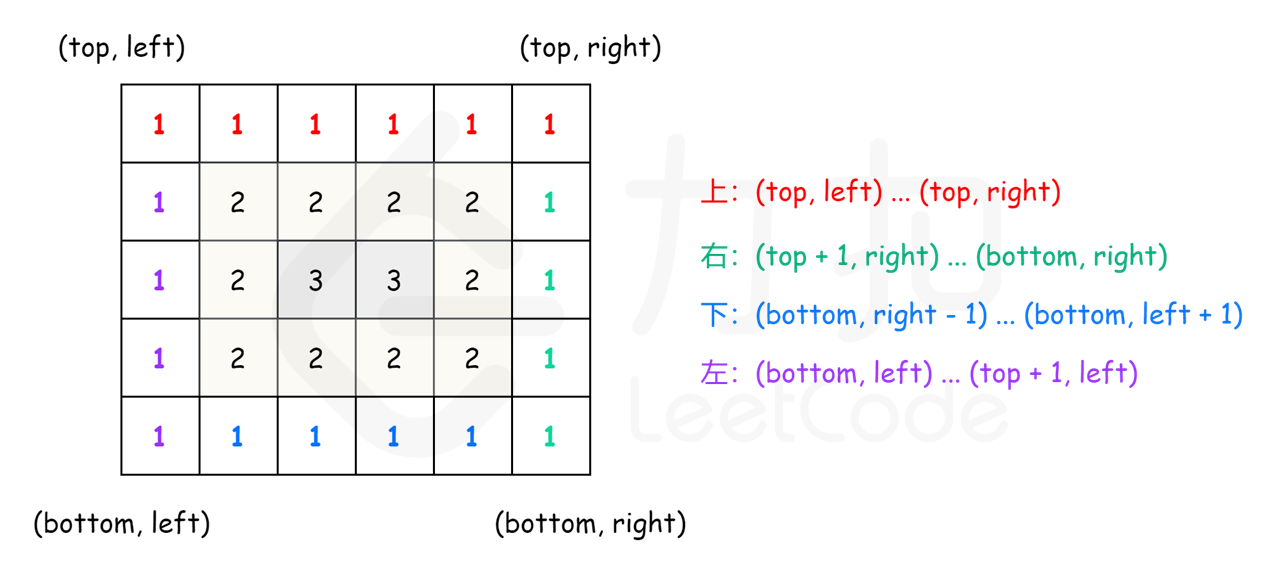
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) {
return {};
}
int rows = matrix.size(), columns = matrix[0].size();
vector<int> order;
int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
while (left <= right && top <= bottom) {
for (int column = left; column <= right; column++) {
order.push_back(matrix[top][column]);
}
for (int row = top + 1; row <= bottom; row++) {
order.push_back(matrix[row][right]);
}
if (left < right && top < bottom) {
for (int column = right - 1; column > left; column--) {
order.push_back(matrix[bottom][column]);
}
for (int row = bottom; row > top; row--) {
order.push_back(matrix[row][left]);
}
}
left++;
right--;
top++;
bottom--;
}
return order;
}
};与上一题不同的是,这次是生成螺旋矩阵了,做法与上一题基本一致,不多bb
- 模拟
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> direct = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
vector<vector<int>> res(n, vector<int>(n));
int x = 0, y = 0, i = 0, count = 1;
res[x][y] = count;
count++;
while (count <= n * n) {
int newx = x + direct[i % 4][0];
int newy = y + direct[i % 4][1];
if (newx >= n || newx < 0 || newy >= n || newy < 0 || res[newx][newy] != 0) {
i++;
continue;
}
else {
res[newx][newy] = count;
count++;
x = newx;
y = newy;
}
}
return res;
}
};- 按层模拟
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
int num = 1;
vector<vector<int>> matrix(n, vector<int>(n));
int left = 0, right = n - 1, top = 0, bottom = n - 1;
while (left <= right && top <= bottom) {
for (int column = left; column <= right; column++) {
matrix[top][column] = num;
num++;
}
for (int row = top + 1; row <= bottom; row++) {
matrix[row][right] = num;
num++;
}
if (left < right && top < bottom) {
for (int column = right - 1; column > left; column--) {
matrix[bottom][column] = num;
num++;
}
for (int row = bottom; row > top; row--) {
matrix[row][left] = num;
num++;
}
}
left++;
right--;
top++;
bottom--;
}
return matrix;
}
};一般是用来判断括号的合法性或者删除无效的括号,可以用栈来做,也可以直接通过数括号的个数来
这个题因为括号不止一种,所以只能通过栈来一个个确认
class Solution {
public:
bool isValid(string s) {
int n = s.size();
if (n % 2 == 1) {
return false;
}
// 这个字典用来区分左右括号的
unordered_map<char, char> pairs = {
{')', '('},
{']', '['},
{'}', '{'}
};
stack<char> stk;
for (char ch: s) {
// 如果是右括号
if (pairs.count(ch)) {
if (stk.empty() || stk.top() != pairs[ch]) {
return false;
}
stk.pop();
}
// 如果是左括号
else {
stk.push(ch);
}
}
return stk.empty();
}
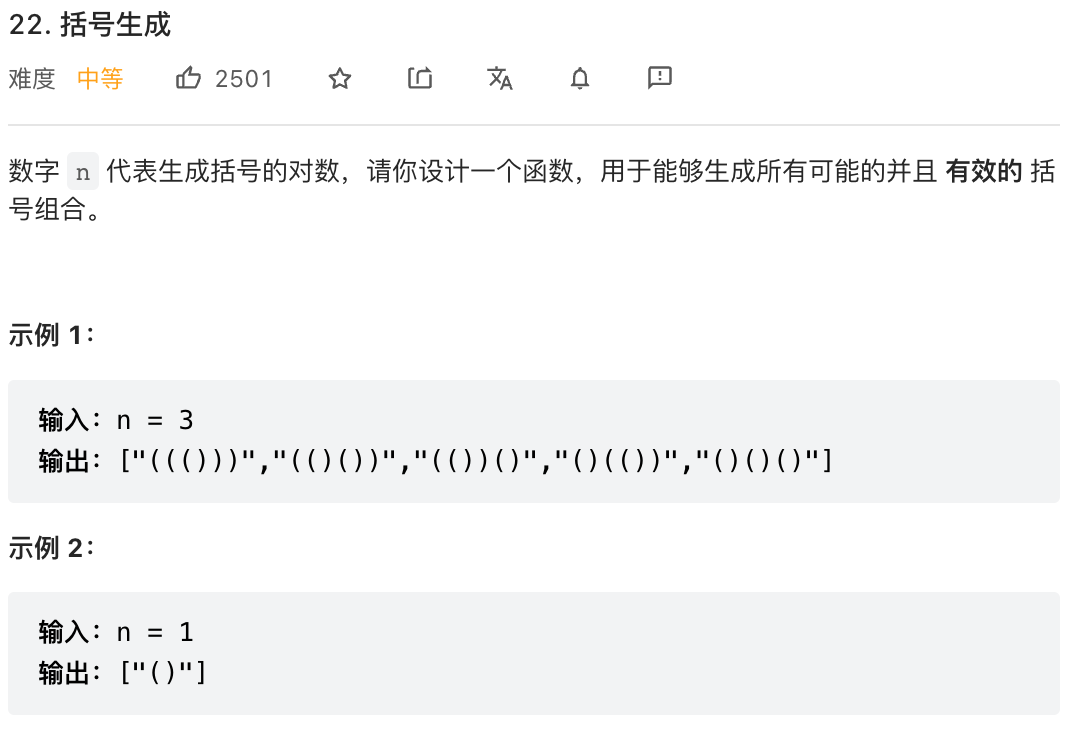
};这题虽然是括号,但是穷举所有可能的情况,这种需要用到回溯的方法,回溯也是需要用到递归的,回溯的一个需要注意的点是,在回溯前做的操作,在回溯后要撤销掉,回溯时要把所有这一步能做的操作都做一遍
class Solution {
void backtrack(vector<string>& ans, string& cur, int open, int close, int n) {
if (cur.size() == n * 2) {
ans.push_back(cur);
return;
}
// *** 这里只能进行两种操作,一种加(,一种加),都要尝试 ***
// 当左括号小于n时才能进行
if (open < n) {
cur.push_back('(');
backtrack(ans, cur, open + 1, close, n);
cur.pop_back();
}
// 同样,右括号个数应该小于左括号个数
if (close < open) {
cur.push_back(')');
backtrack(ans, cur, open, close + 1, n);
cur.pop_back();
}
// *** 尝试结束 ***
}
public:
vector<string> generateParenthesis(int n) {
vector<string> result;
string current;
backtrack(result, current, 0, 0, n);
return result;
}
};看到最长两个字,应当想到是否可以采用动态规划dp来做,当然也可以用栈来做
- dp
class Solution {
public:
int longestValidParentheses(string s) {
int maxans = 0, n = s.length();
vector<int> dp(n, 0);
for (int i = 1; i < n; i++) {
if (s[i] == ')') {
if (s[i - 1] == '(') {
dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
} else if (i - dp[i - 1] > 0 && s[i - dp[i - 1] - 1] == '(') {
dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
}
maxans = max(maxans, dp[i]);
}
}
return maxans;
}
};- 栈
先入栈一个-1,保证开头的括号正确时能计算出长度,后续如果栈为空时,也需要入栈一个当前位置作为计算长度的起始点。
class Solution {
public:
int longestValidParentheses(string s) {
int maxans = 0;
stack<int> stk;
stk.push(-1);
for (int i = 0; i < s.length(); i++) {
if (s[i] == '(') {
stk.push(i);
} else {
stk.pop();
if (stk.empty()) {
stk.push(i);
} else {
maxans = max(maxans, i - stk.top());
}
}
}
return maxans;
}
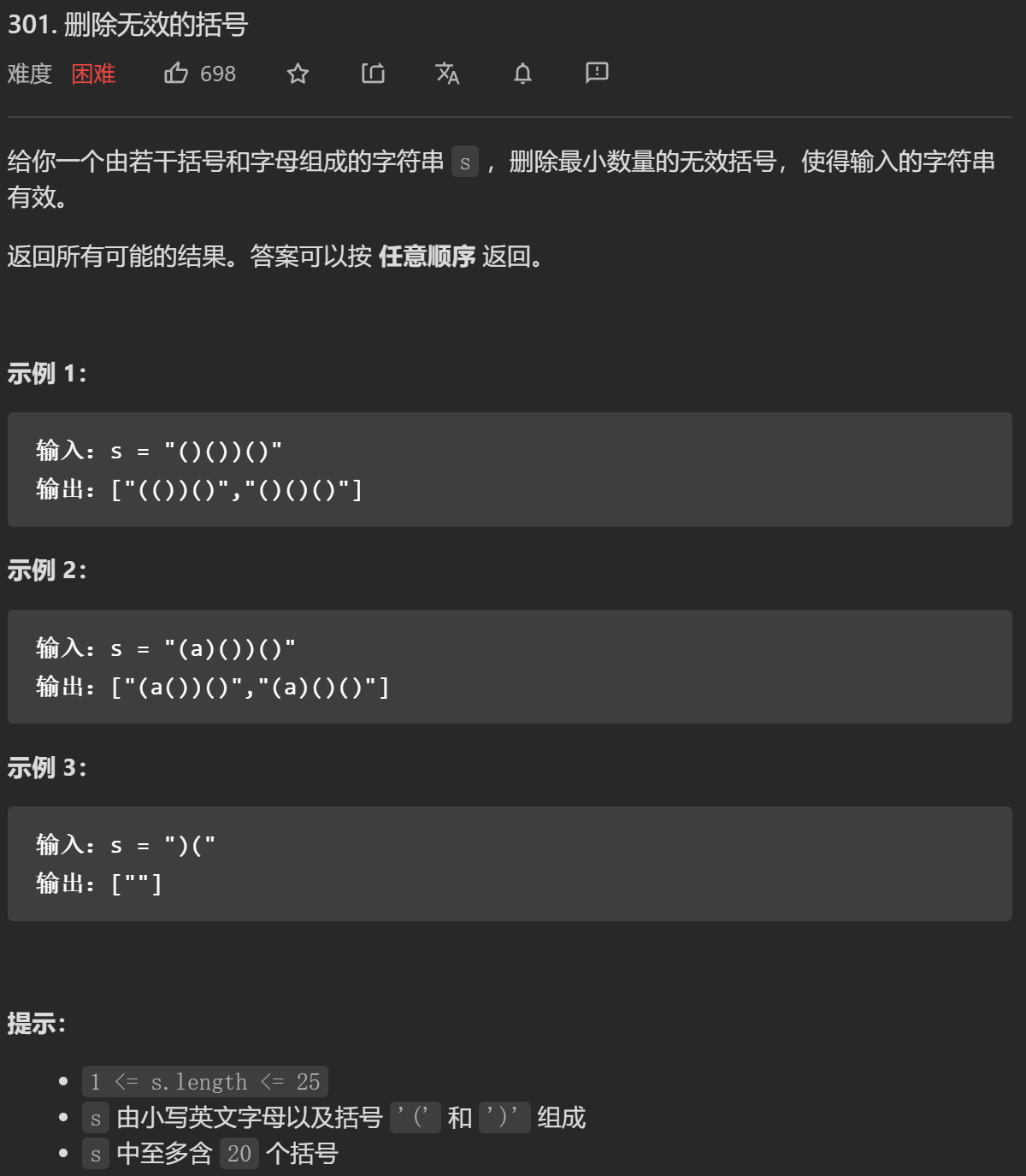
};- 注意这个返回所有可能的结果,遇到这种情况一般都需要用到回溯
- 当遇到这种只有一种括号类型的需要判断是否合法时,可以通过左右括号的个数来简易判断,如果遍历过程中,右括号个数大于左括号个数则不合法,否则最终判断左括号个数是否等于右括号个数
- 首先统计左右括号个数,得出需要删除几个左括号或几个右括号
- 然后回溯来进行删除并判断是否合法,其中一些确定不需要回溯的情况可以剪枝掉加快速度
class Solution {
public:
vector<string> res;
// 判断字符串的括号是否合法
bool isValid(const string& str) {
int cnt = 0;
for (auto& c : str) {
if (c == '(') {
cnt++;
}
else if (c == ')') {
cnt--;
if (cnt < 0) return false;
}
}
return cnt == 0;
}
vector<string> removeInvalidParentheses(string s) {
int lremove = 0, rremove = 0;
for (auto& c: s) {
if (c == '(') {
lremove++;
}
else if (c == ')') {
if (lremove > 0) {
lremove--;
}
else {
rremove++;
}
}
}
backTrack(s, 0, lremove, rremove);
return res;
}
// 回溯
void backTrack(string s, int start, int lremove, int rremove) {
// 如果左右括号都不需要再删除了,判断字符串是否合法
if (lremove == 0 && rremove == 0) {
if (isValid(s)) {
res.push_back(s);
}
return;
}
for (int i = start; i < s.size(); i++) {
// 如果左右括号需要删除的数目比当前字符串还多,则无需继续回溯了
if (lremove + rremove > s.size()) return;
// 剪枝,如果i和i-1字符相同,则无需再进行一遍
if (i != start && s[i] == s[i - 1]) continue;
// 删除左括号
if (lremove > 0 && s[i] == '(') {
backTrack(s.substr(0, i) + s.substr(i+1), i, lremove - 1, rremove);
}
// 删除右括号
if (rremove > 0 && s[i] == ')') {
backTrack(s.substr(0, i) + s.substr(i+1), i, lremove, rremove - 1);
}
}
}
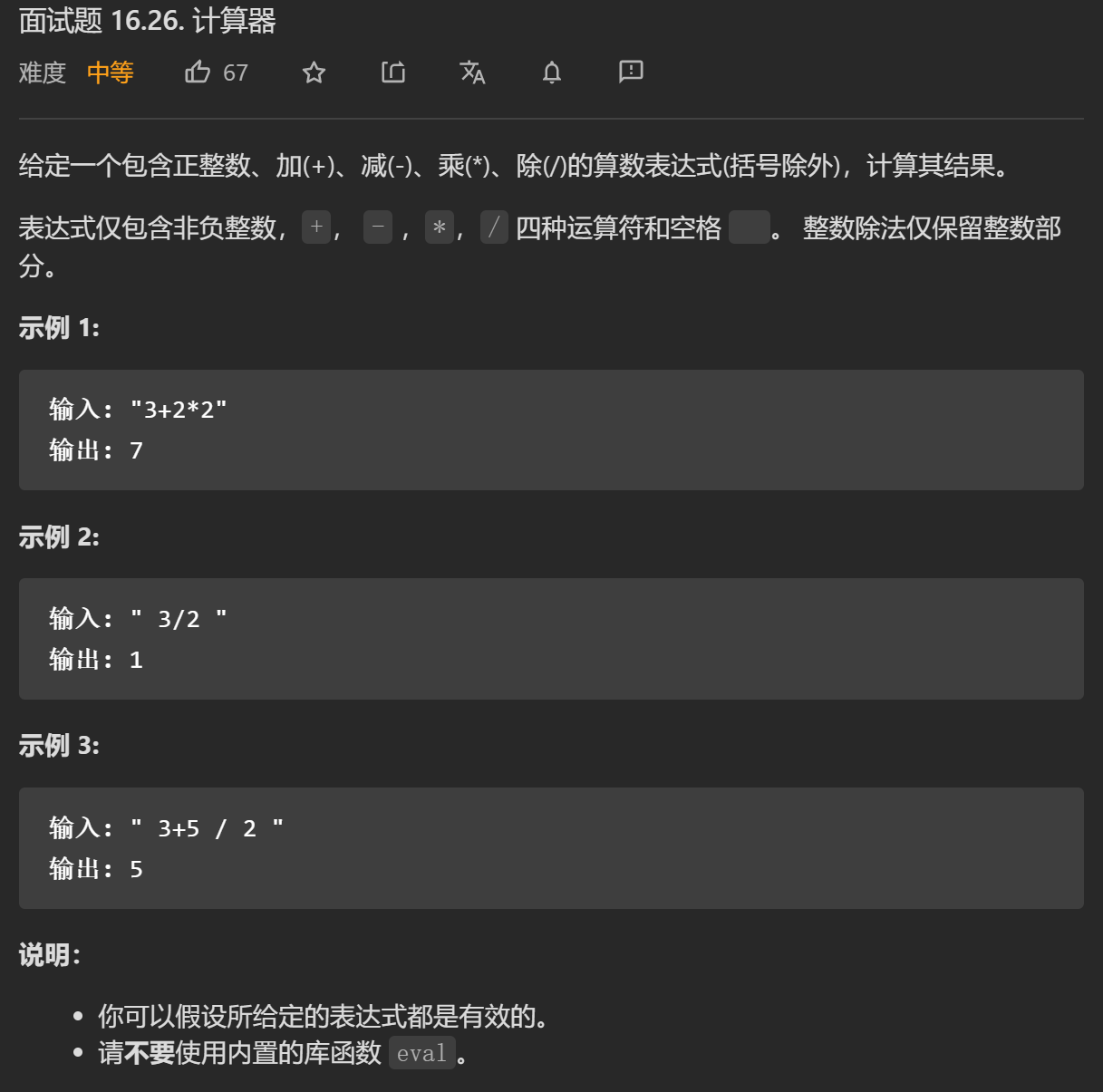
};class Solution {
public:
int calculate(string s) {
stack<int> sta;
char c = '+';
int num = 0;
for(int i = 0; i <= s.length(); i++){ //这里是i<=s.length();一定要有等号!!!读完数据最后一位'\0'进行最后一次计算
if(isdigit(s[i])){ // C 库函数 int isdigit(int c) 检查所传的字符是否是十进制数字字符
num = num * 10 + (s[i] - '0');
}else if(isspace(s[i])){ // C 库函数 int isspace(int c) 检查所传的字符是否是空白字符,包括' ','\t','\n','\v','\f','\r'
continue;
}else{
switch(c){
case '+':
sta.push(num);
break;
case '-':
sta.push(-num);
break;
case '*':
num*=sta.top();
sta.pop();
sta.push(num);
break;
case '/':
num=sta.top()/num;
sta.pop();
sta.push(num);
break;
}
num=0;
c=s[i];
}
}
int res=0;
while(!sta.empty()){
res+=sta.top();
sta.pop();
}
return res;
}
};回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
- 回溯的题目都是比较有难度的,通常在middle到hard,一般通过返回所有可能的结果这种情况判断
- 注意回溯的一个特点是,在回溯到一种可能的情况后要将之前做的操作抹除掉,防止一步做了多次操作
- 回溯有时候可以通过剪枝去掉一些不可能的分支情况,用于提高运行速度
用回溯算法解决问题的一般步骤:
- 针对所给问题,定义问题的解空间,它至少包含问题的一个(最优)解。
- 确定易于搜索的解空间结构,使得能用回溯法方便地搜索整个解空间 。
- 以深度优先的方式搜索解空间,并且在搜索过程中用剪枝函数避免无效搜索。
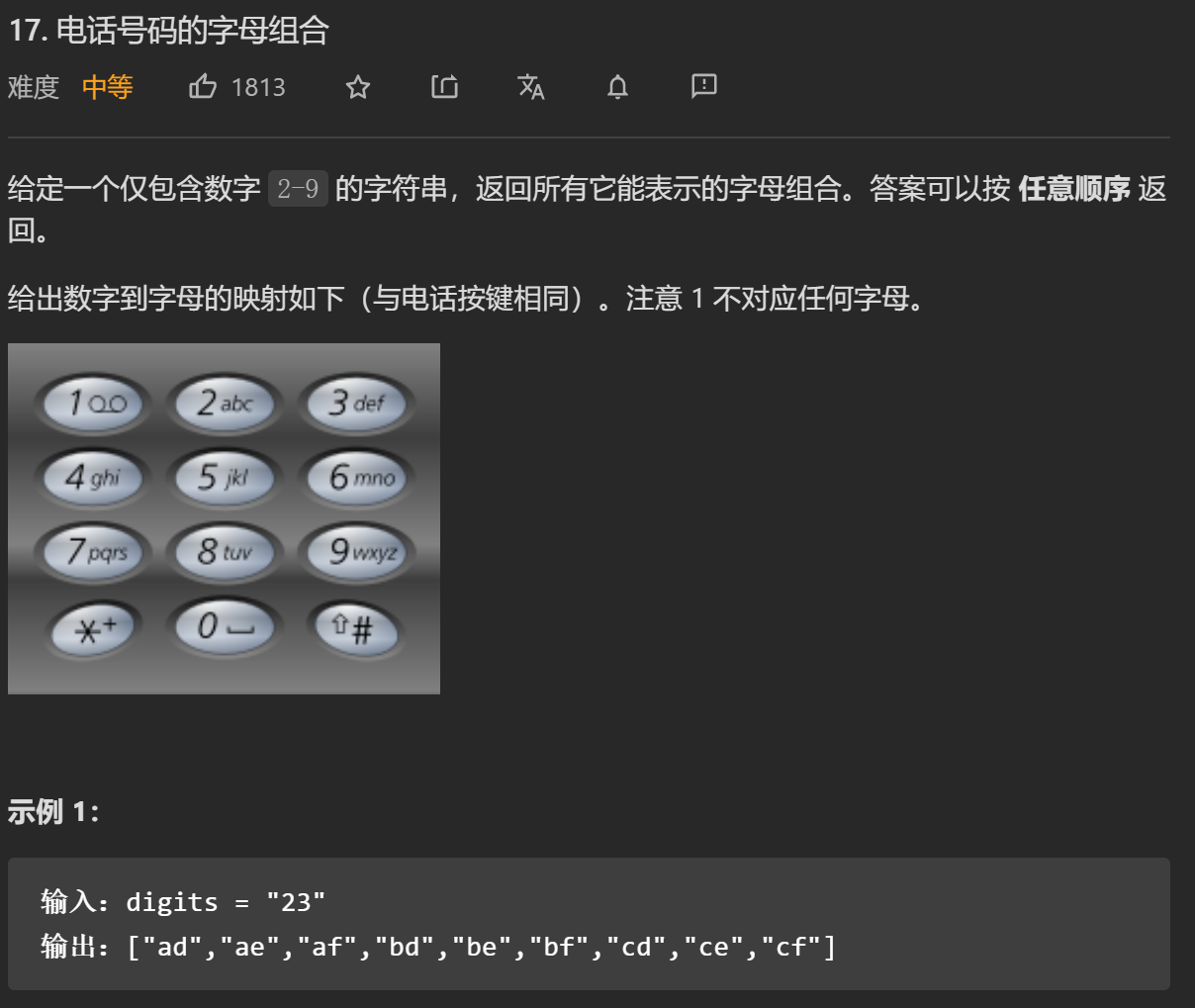
class Solution {
private:
unordered_map<char, string> numbers = {{'2', "abc"},
{'3', "def"},
{'4', "ghi"},
{'5', "jkl"},
{'6', "mno"},
{'7', "pqrs"},
{'8', "tuv"},
{'9', "wxyz"}};
vector<string> res;
public:
void backTrack(string digits, int start, string& str) {
if (start == digits.size()) {
res.push_back(str);
}
else {
// 注意这里千万不能从start开始遍历到digits.size(),会导致后面的情况下缺失前面的部分
// 比如输入23,会产生'd' 'e' 'f' 三个多余的结果
for (auto& c: numbers[digits[start]]) {
str.push_back(c);
backTrack(digits, start + 1, str);
str.pop_back();
}
}
}
vector<string> letterCombinations(string digits) {
if (!digits.empty()) {
string s = "";
backTrack(digits, 0, s);
}
return res;
}
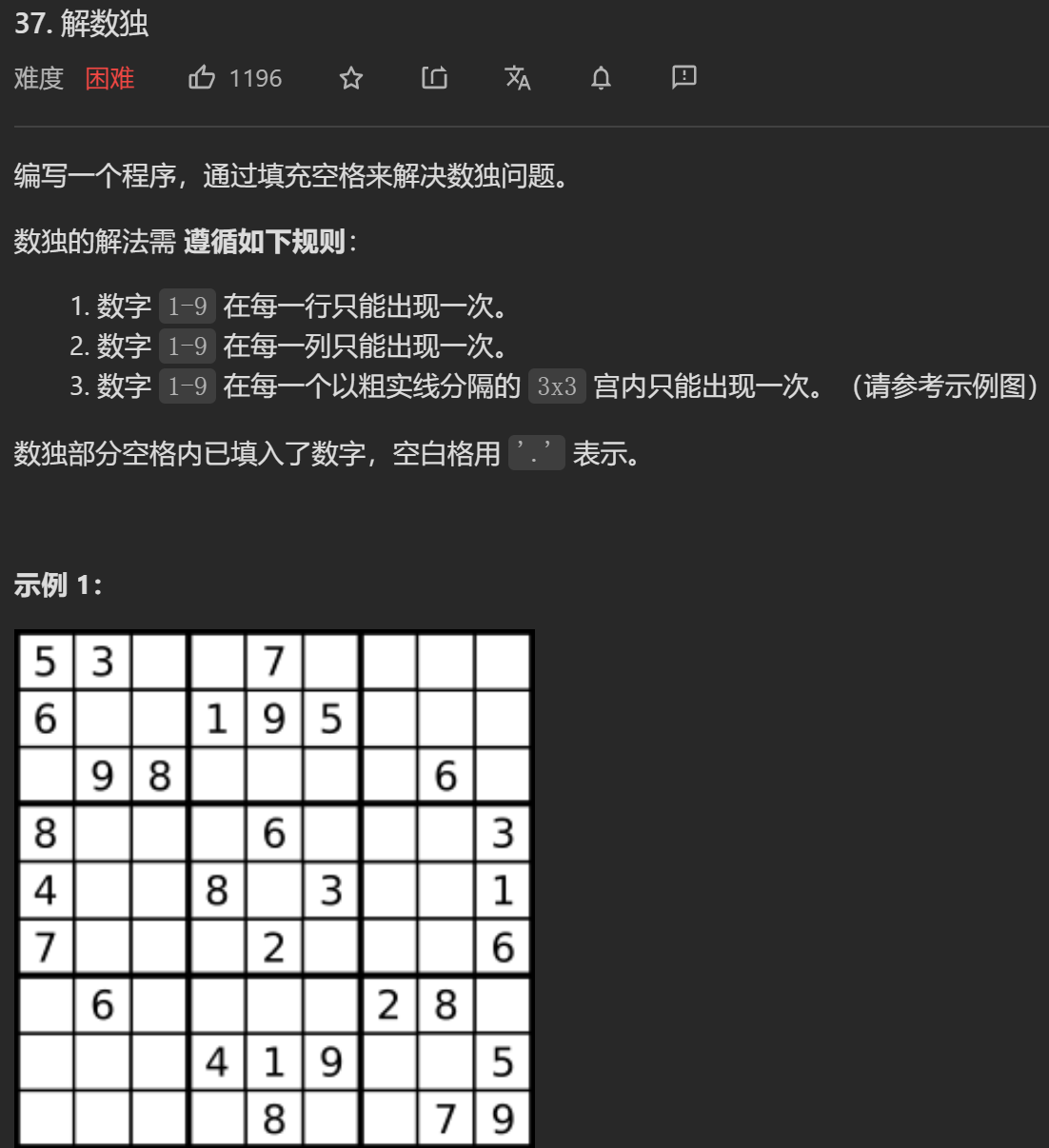
};class Solution {
private:
// line[x][y]表示第x-1行是否出现过y-1数字
bool line[9][9];
// column[x][y]表示第x-1列是否出现过y-1数字
bool column[9][9];
// block[x][y][z]表示第x-1行第y-1个块是否出现过z-1数字
bool block[3][3][9];
// 用于记录是否将空位全部填满
bool valid;
// spaces用于保存需要填数字的位置
vector<pair<int, int>> spaces;
public:
void dfs(vector<vector<char>>& board, int pos) {
// 当空格全部填满,valid = true并返回
if (pos == spaces.size()) {
valid = true;
return;
}
// 取出需要填的空格
auto [i, j] = spaces[pos];
// 遍历可以填的数字
for (int digit = 0; digit < 9 && !valid; ++digit) {
// 当满足所有限制条件时,才可以填这个数
if (!line[i][digit] && !column[j][digit] && !block[i / 3][j / 3][digit]) {
// 填数并将状态更新
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = true;
board[i][j] = digit + '0' + 1;
dfs(board, pos + 1);
// 回溯时要将之前做的操作还原
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = false;
}
}
}
void solveSudoku(vector<vector<char>>& board) {
memset(line, false, sizeof(line));
memset(column, false, sizeof(column));
memset(block, false, sizeof(block));
valid = false;
for (int i = 0; i < 9; ++i) {
for (int j = 0; j < 9; ++j) {
// 如果当前位置是空格,则加入spaces
if (board[i][j] == '.') {
spaces.emplace_back(i, j);
}
// 如果当前是数字,则更新line column block对应位置为true
else {
int digit = board[i][j] - '0' - 1;
line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = true;
}
}
}
// 开始回溯
dfs(board, 0);
}
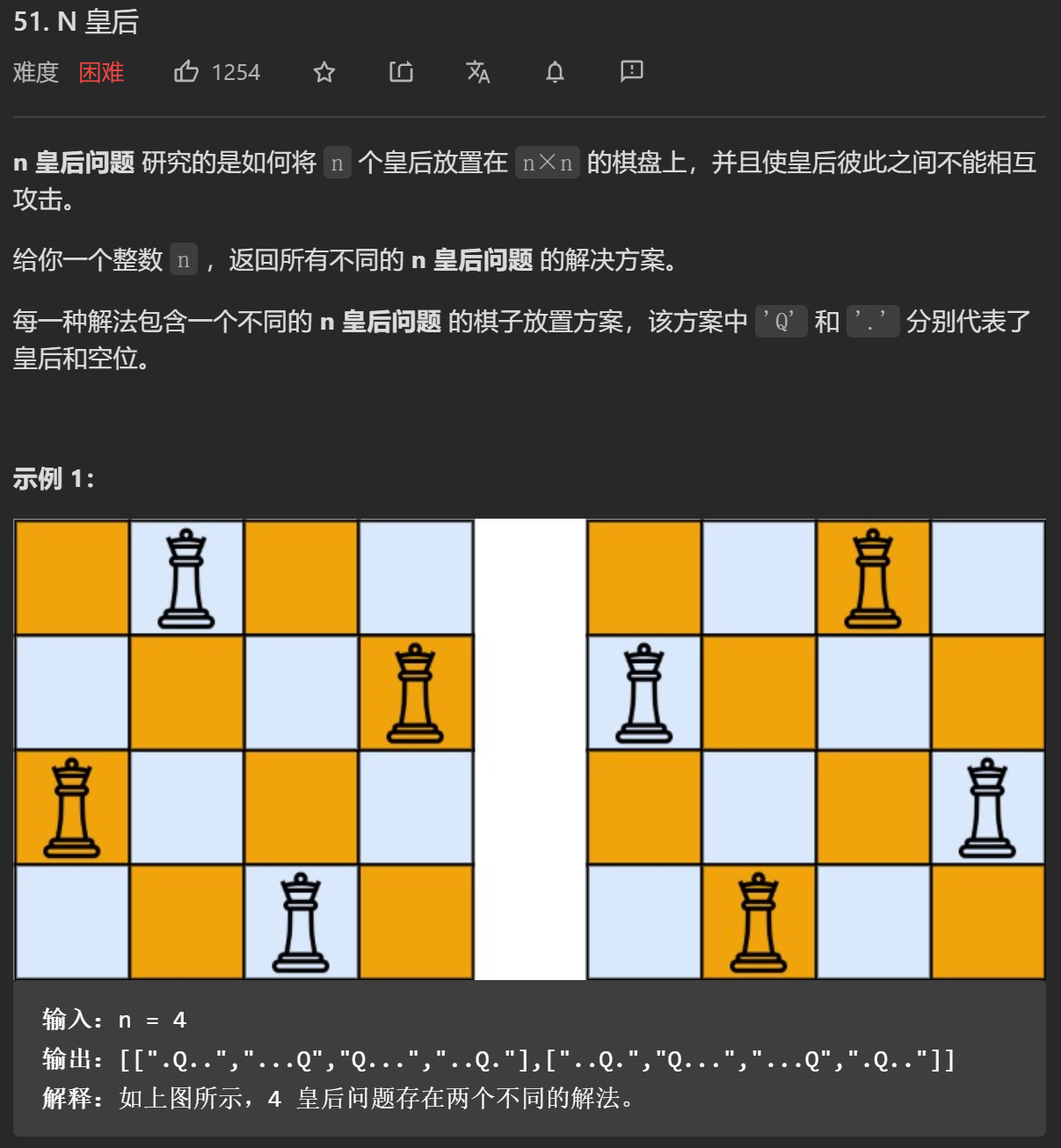
};再来一题与上题类似的典型问题,N皇后
因为皇后是可以横竖斜着走的,我们要让所有的皇后不能互相攻击,就要让每个皇后的行、列、斜对角线均没有其他皇后
回溯的具体做法是:使用一个数组记录每行放置的皇后的列下标,依次在每一行放置一个皇后。每次新放置的皇后都不能和已经放置的皇后之间有攻击:即新放置的皇后不能和任何一个已经放置的皇后在同一列以及同一条斜线上,并更新数组中的当前行的皇后列下标。当 N 个皇后都放置完毕,则找到一个可能的解。当找到一个可能的解之后,将数组转换成表示棋盘状态的列表,并将该棋盘状态的列表加入返回列表。
由于每个皇后必须位于不同列,因此已经放置的皇后所在的列不能放置别的皇后。第一个皇后有 N 列可以选择,第二个皇后最多有 N-1 列可以选择,第三个皇后最多有 N-2 列可以选择(如果考虑到不能在同一条斜线上,可能的选择数量更少),因此所有可能的情况不会超过 N! 种,遍历这些情况的时间复杂度是 O(N!)。
为了降低总时间复杂度,每次放置皇后时需要快速判断每个位置是否可以放置皇后,显然,最理想的情况是在 O(1) 的时间内判断该位置所在的列和两条斜线上是否已经有皇后。
class Solution {
public:
vector<vector<string>> solveNQueens(int n) {
auto solutions = vector<vector<string>>(); // 最终结果
auto queens = vector<int>(n, -1); // 每一行的皇后所在列数
auto columns = unordered_set<int>(); // 是否在一列
auto diagonals1 = unordered_set<int>(); // 是否在右斜线上
auto diagonals2 = unordered_set<int>(); // 是否在左斜线上
backtrack(solutions, queens, n, 0, columns, diagonals1, diagonals2);
return solutions;
}
// 回溯,每次填一行的皇后,row表示当前要填的行
void backtrack(vector<vector<string>> &solutions, vector<int> &queens, int n, int row, unordered_set<int> &columns, unordered_set<int> &diagonals1, unordered_set<int> &diagonals2) {
// 当row到达n时,说明0到n-1都填完了,说明已经完成了一个可行解
if (row == n) {
vector<string> board = generateBoard(queens, n);
solutions.push_back(board);
} else {
// 从0到n-1遍历第row行可能插入皇后的列
for (int i = 0; i < n; i++) {
// 如果这一列有其他皇后了,跳过
if (columns.find(i) != columns.end()) {
continue;
}
// 如果这一左斜对角有其他皇后了,跳过
int diagonal1 = row - i;
if (diagonals1.find(diagonal1) != diagonals1.end()) {
continue;
}
// 如果这一右斜对角有其他皇后了,跳过
int diagonal2 = row + i;
if (diagonals2.find(diagonal2) != diagonals2.end()) {
continue;
}
// 如果均满足条件,则将皇后填到这个位置,并更新状态
queens[row] = i;
columns.insert(i);
diagonals1.insert(diagonal1);
diagonals2.insert(diagonal2);
// 进行下一行皇后的放置
backtrack(solutions, queens, n, row + 1, columns, diagonals1, diagonals2);
// 回溯,取消皇后的放置并重置状态
queens[row] = -1;
columns.erase(i);
diagonals1.erase(diagonal1);
diagonals2.erase(diagonal2);
}
}
}
// 根据皇后的放置位置进行棋盘矩阵的绘制
vector<string> generateBoard(vector<int> &queens, int n) {
auto board = vector<string>();
for (int i = 0; i < n; i++) {
string row = string(n, '.');
row[queens[i]] = 'Q';
board.push_back(row);
}
return board;
}
};不难发现这题与解数独基本一致,需要知道的是:
- 斜对角的状态该如何保存
- 遍历可能存在的位置时要如何过滤掉错误的位置(通过多个状态进行过滤)
- 回溯后切记要恢复之前的状态。
一样的题,只不过不用返回棋盘了,返回解的个数
class Solution {
public:
int res = 0;
int totalNQueens(int n) {
unordered_set<int> col;
unordered_set<int> left_diagonal;
unordered_set<int> right_diagonal;
backTrack(n, 0, col, left_diagonal, right_diagonal);
return res;
}
void backTrack(const int& n, int row, unordered_set<int>& col, unordered_set<int>& left_diagonal, unordered_set<int>& right_diagonal) {
// 当row到达n时,说明0到n-1都填完了,说明已经完成了一个可行解
if (row == n) {
res++;
return;
}
else {
// 从0到n-1遍历第row行可能插入皇后的列
for (int i = 0; i < n; i++) {
// 如果这一列有其他皇后了,跳过
if (col.count(i)) {
continue;
}
// 如果这一左斜对角有其他皇后了,跳过
if (left_diagonal.count(row - i)) {
continue;
}
// 如果这一右斜对角有其他皇后了,跳过
if (right_diagonal.count(row + i)) {
continue;
}
// 这个位置可以放置皇后,更新状态
col.insert(i);
left_diagonal.insert(row - i);
right_diagonal.insert(row + i);
// 进行下一行皇后的放置
backTrack(n, row + 1, col, left_diagonal, right_diagonal);
// 回溯,取消皇后的放置并重置状态
col.erase(i);
left_diagonal.erase(row - i);
right_diagonal.erase(row + i);
}
}
}
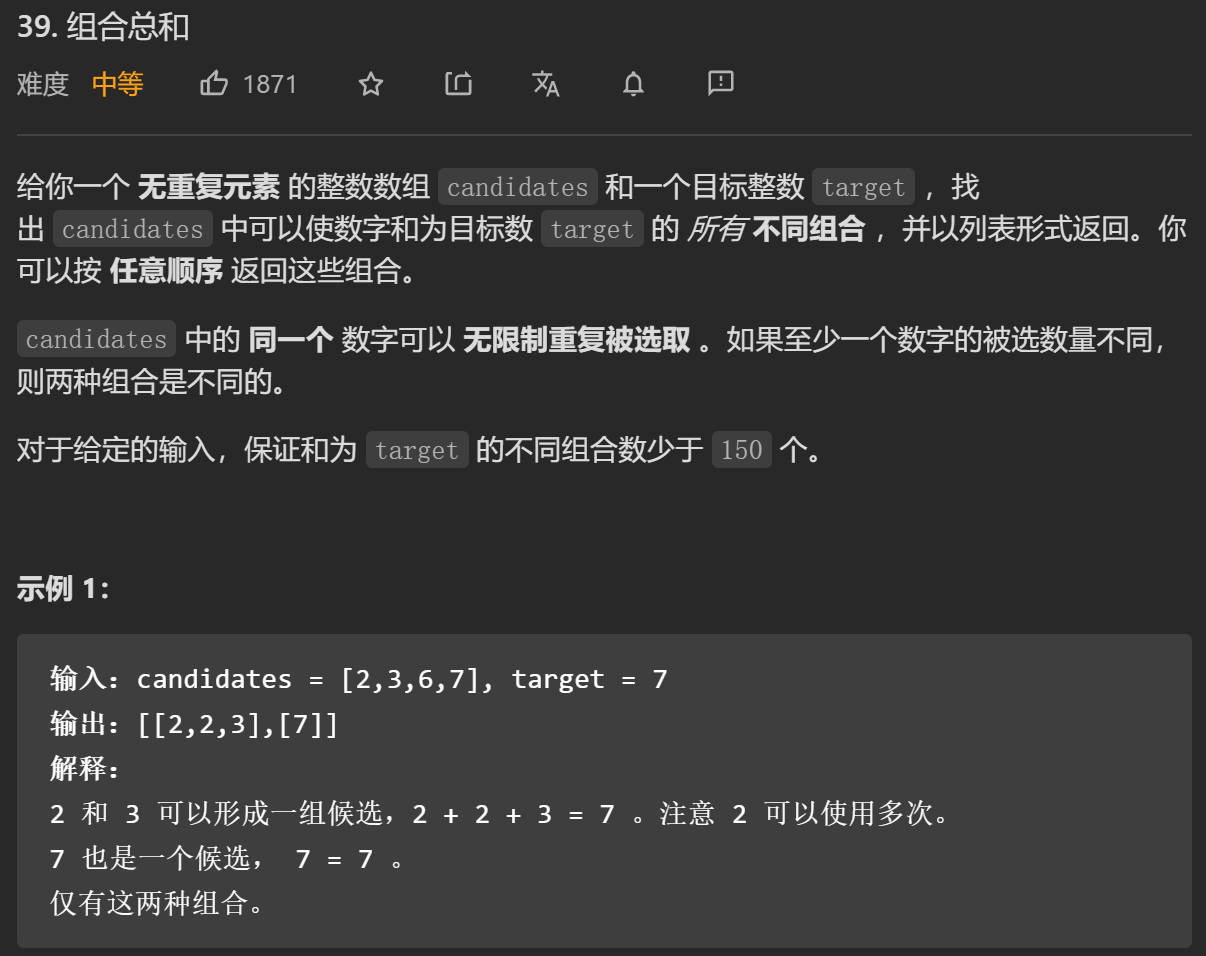
};这题题目限制了正整数,所以可以通过candidates[i] <= target来进行剪枝,避免不必要的遍历。
class Solution {
private:
vector<vector<int>> res;
vector<int> midres;
public:
void dfs(vector<int>& candidates, int target, int start, vector<int>& midres) {
if (target == 0) {
res.emplace_back(midres);
return;
}
for (int i = start; i < candidates.size(); i++) {
// 小于target的正整数才需要遍历
if (candidates[i] <= target) {
midres.emplace_back(candidates[i]);
dfs(candidates, target - candidates[i], i, midres);
midres.pop_back();
}
}
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
dfs(candidates, target, 0, midres);
return res;
}
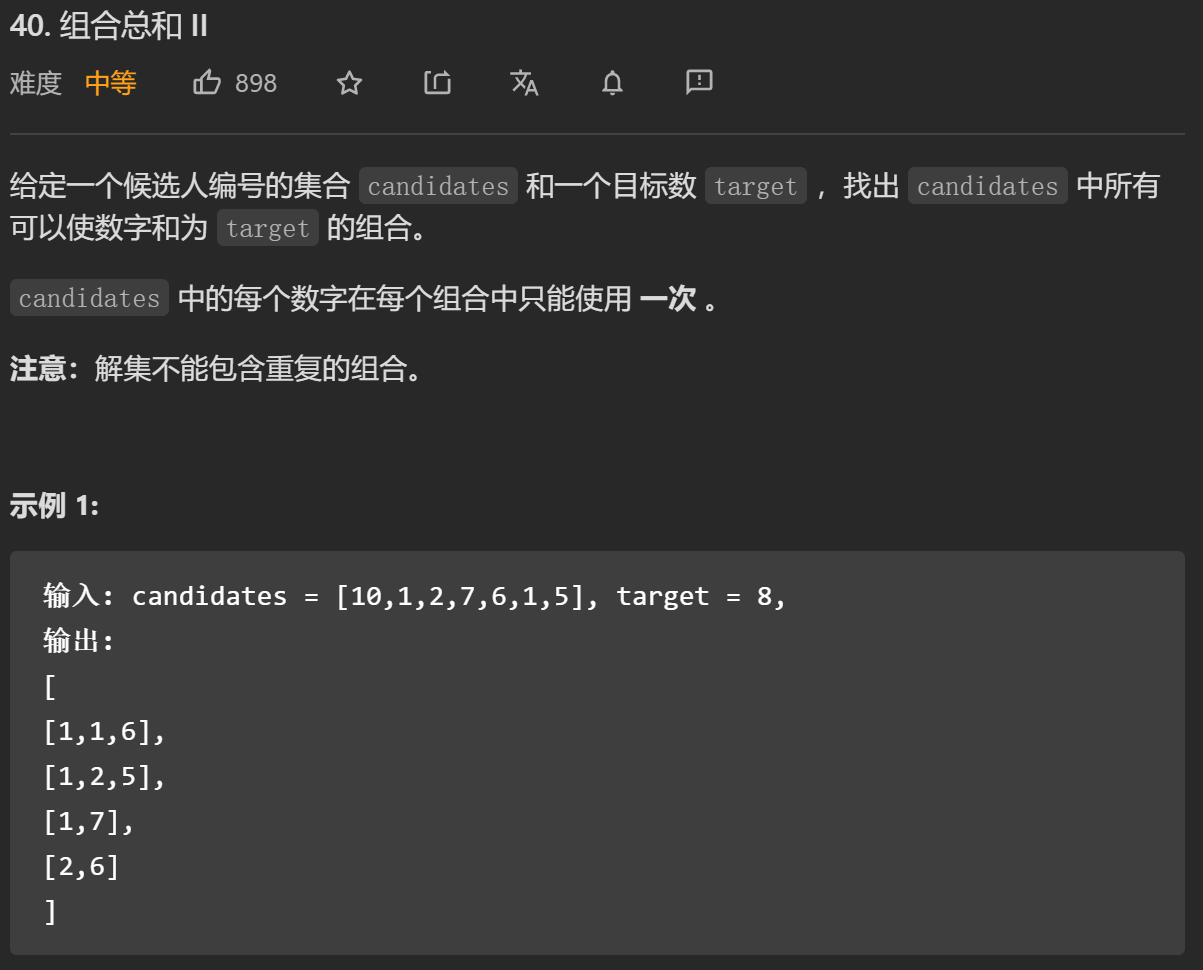
};这题与上面的不同在于,每个数字只能取一次,且结果不能有重复的。我们只需要把递归的条件从i变成i+1,且在循环时加上一句判断if(i > start && candidates[i] == candidates[i-1]) continue;避免重复情况出现即可。
class Solution {
private:
vector<vector<int>> res;
vector<int> midres;
public:
void dfs(vector<int>& candidates, int target, int start, vector<int>& midres) {
if (target == 0) {
res.emplace_back(midres);
return;
}
// 因为candidates排过序,所以candidates[i] <= target的判断放在循环条件里,如果不满足则后面的都不满足
for (int i = start; i < candidates.size() && candidates[i] <= target; i++) {
// 避免重复情况出现
if (i > start && candidates[i] == candidates[i - 1])
continue;
midres.emplace_back(candidates[i]);
// 注意这里需要把i变成i+1,因为不能重复取一个数多次
dfs(candidates, target - candidates[i], i + 1, midres);
midres.pop_back();
}
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
// 排序让相同的数排列在一起
sort(candidates.begin(), candidates.end());
dfs(candidates, target, 0, midres);
return res;
}
};class Solution {
vector<int> vis;
public:
void backtrack(vector<int>& nums, vector<vector<int>>& ans, int idx, vector<int>& perm) {
if (idx == nums.size()) {
ans.emplace_back(perm);
return;
}
for (int i = 0; i < (int)nums.size(); ++i) {
if (vis[i] || (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])) {
continue;
}
perm.emplace_back(nums[i]);
vis[i] = 1;
backtrack(nums, ans, idx + 1, perm);
vis[i] = 0;
perm.pop_back();
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<vector<int>> ans;
vector<int> perm;
vis.resize(nums.size());
sort(nums.begin(), nums.end());
backtrack(nums, ans, 0, perm);
return ans;
}
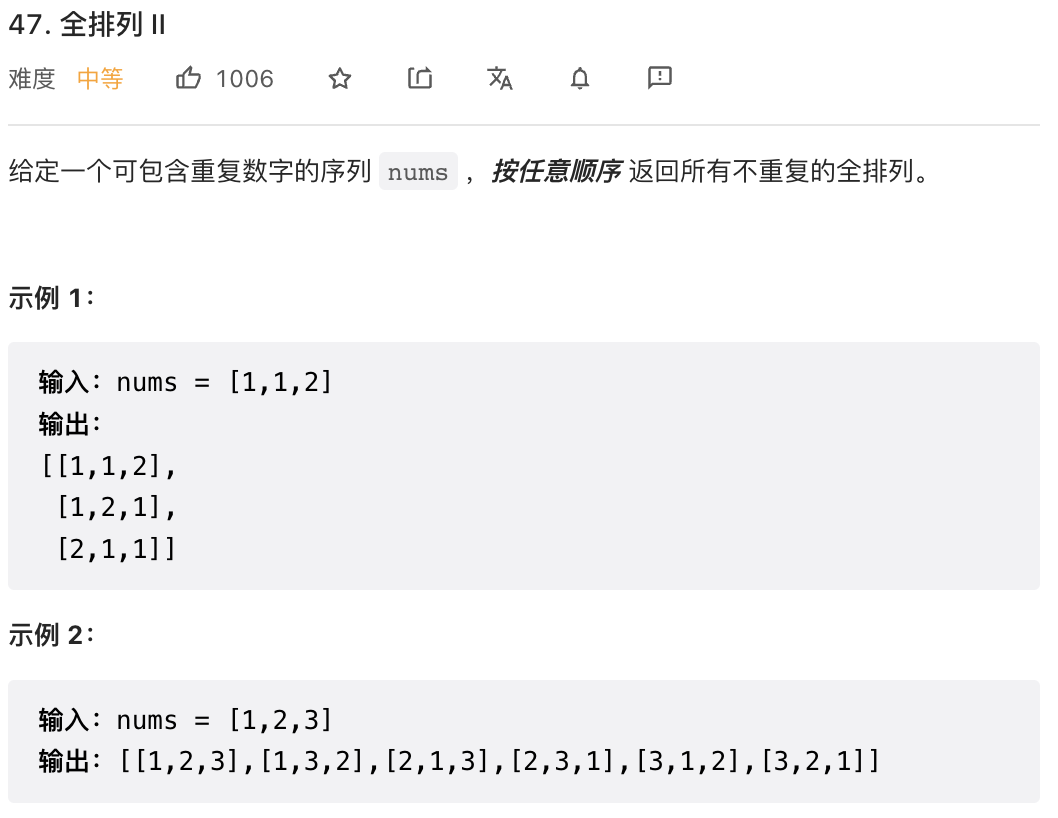
};这里解释一下为什么加了i > 0 && nums[i] == nums[i - 1] && !vis[i - 1]这个条件就可以限制重复结果的产生了:
加上 !vis[i - 1]来去重主要是通过限制一下两个相邻的重复数字的访问顺序
举个栗子,对于两个相同的数11,我们将其命名为1a 1b, 1a表示第一个1,1b表示第二个1; 那么,不做去重的话,会有两种重复排列 1a1b, 1b1a, 我们只需要取其中任意一种排列; 为了达到这个目的,限制一下1a, 1b访问顺序即可。 比如我们只取1a1b那个排列的话,只有当visit nums[i-1]之后我们才去visit nums[i], 也就是如果!visited[i-1]的话则continue
注意剪枝,其他没啥
class Solution {
public:
vector<vector<int>> res;
vector<vector<int>> combine(int n, int k) {
vector<int> mid_res;
backTrack(n, k, 1, 0, mid_res);
return res;
}
void backTrack(int n, int k, int start, int count, vector<int>& mid_res) {
// 剪枝
if (count + (n - start + 1) < k)
return;
if (count == k) {
res.push_back(mid_res);
return;
}
for (int i = start; i <= n; i++) {
mid_res.push_back(i);
backTrack(n, k, i + 1, count + 1, mid_res);
mid_res.pop_back();
}
}
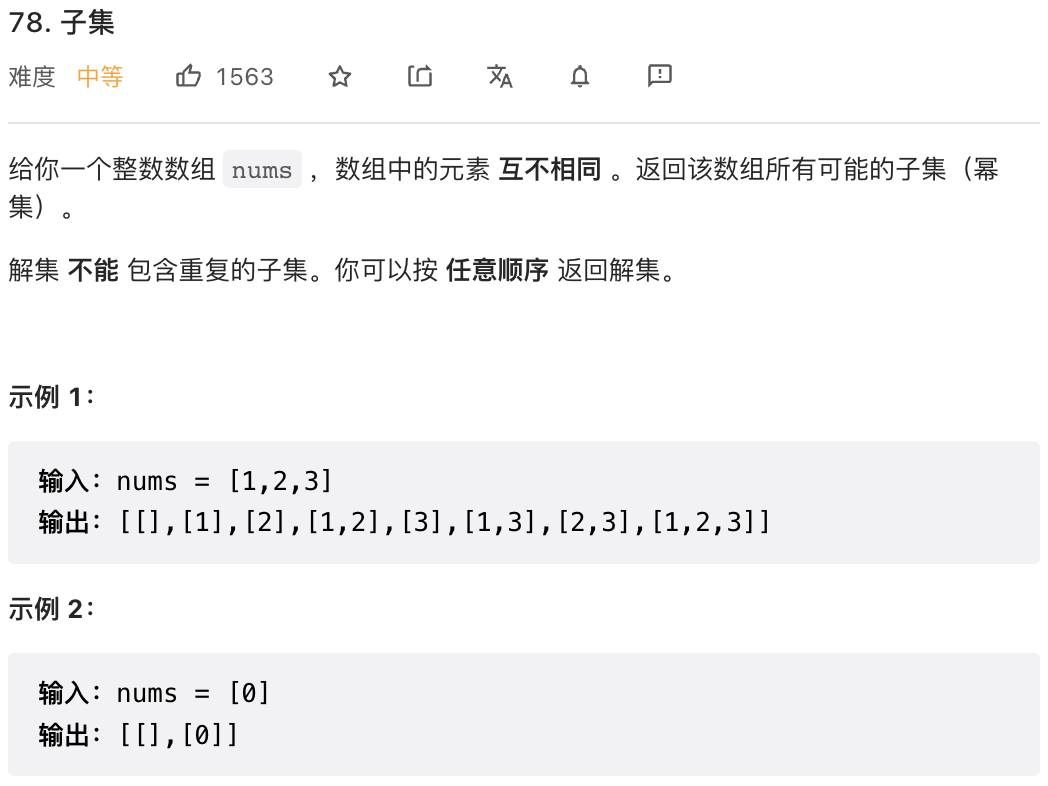
};这里有点不一样,当前元素可选可不选
class Solution {
private:
vector<vector<int>> res;
vector<int> mid_res;
public:
void dfs(vector<int>& nums,int start){
// 因为要取所有子集,所以每次dfs(当前元素选或者不选)都要加入结果
res.push_back(mid_res);
// 满足条件结束dfs
if(start == nums.size()) return ;
// 对于没选过的元素进行遍历
for(int i = start; i < nums.size(); ++i){
mid_res.push_back(nums[i]);
dfs(nums, i + 1);
mid_res.pop_back();
}
}
vector<vector<int>> subsets(vector<int>& nums) {
dfs(nums, 0);
return res;
}
};class Solution {
private:
vector<vector<int>> res;
vector<int> mid_res;
public:
void dfs(vector<int>& nums,int start){
// 因为要取所有子集,所以每次dfs(当前元素选或者不选)都要加入结果
res.push_back(mid_res);
// 满足条件结束dfs
if(start == nums.size()) return ;
// 对于没选过的元素进行遍历
for(int i = start; i < nums.size(); ++i){
// 如果nums[i] == nums[i-1]再选会产生重复结果,因此跳过
if(i > start && nums[i] == nums[i-1])
continue;
mid_res.push_back(nums[i]);
dfs(nums, i + 1);
mid_res.pop_back();
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
sort(nums.begin(),nums.end());
dfs(nums, 0);
return res;
}
};class Solution {
public:
// 可以遍历的四个方向
vector<pair<int, int>> direction = {{0, -1},
{-1, 0},
{0, 1},
{1, 0}};
bool exist(vector<vector<char>>& board, string word) {
vector<vector<int>> visited(board.size(), vector<int>(board[0].size()));
// 要对每个元素都作为起始点进行遍历
for (int i = 0; i < board.size(); i++) {
for (int j = 0; j < board[0].size(); j++) {
if (backTrack(board, visited, word, 0, i, j))
return true;
}
}
return false;
}
bool backTrack(vector<vector<char>>& board, vector<vector<int>>& visited, string word, int ind,
int x, int y) {
if (board[x][y] != word[ind])
{
return false;
}
else if (ind == word.size() - 1) {
return true;
}
// 当不满足上述true或者false的条件时,说明是在遍历途中
// 取当前元素
visited[x][y] = 1;
bool result = false;
// 朝四个方向遍历
for (int i = 0; i < 4; i++) {
int newx = x + direction[i].first;
int newy = y + direction[i].second;
// 只取边界范围内的未遍历过的元素
if (newx >= 0 && newx < board.size() && newy >= 0 && newy < board[0].size()) {
if (!visited[newx][newy]) {
// 如果成功了,则返回
if (backTrack(board, visited, word, ind + 1, newx, newy)) {
result = true;
break;
}
}
}
}
// 如果四个方向均不行,则这个元素不对,回溯到上一个元素,这个元素的状态恢复
visited[x][y] = 0;
return result;
}
};这题不算回溯,就是单纯地利用二叉树的性质去递归,写一个递归函数用于生成所有可能存在的结果集合,然后分别递归调用生成左子树结果集合和右子树结果集合,然后分别从这两个集合中取出来组成结果即可
class Solution {
public:
vector<TreeNode*> generateTrees(int start, int end) {
if (start > end) {
return { nullptr };
}
vector<TreeNode*> allTrees;
// 枚举可行根节点
for (int i = start; i <= end; i++) {
// 获得所有可行的左子树集合
vector<TreeNode*> leftTrees = generateTrees(start, i - 1);
// 获得所有可行的右子树集合
vector<TreeNode*> rightTrees = generateTrees(i + 1, end);
// 从左子树集合中选出一棵左子树,从右子树集合中选出一棵右子树,拼接到根节点上
for (auto& left : leftTrees) {
for (auto& right : rightTrees) {
TreeNode* currTree = new TreeNode(i);
currTree->left = left;
currTree->right = right;
allTrees.emplace_back(currTree);
}
}
}
return allTrees;
}
vector<TreeNode*> generateTrees(int n) {
if (!n) {
return {};
}
return generateTrees(1, n);
}
};这题要分位置来看,每个位置选或者不选两种情况,同时要注意满足递增且不重复的条件
一开始想着用之前的方法,每一步都循环后面所有的元素去遍历,然后通过visited+前后元素是否相同来去重,结果有些例子通不过
class Solution {
public:
vector<vector<int>> res;
vector<vector<int>> findSubsequences(vector<int>& nums) {
vector<int> mid_res;
backTrack(nums, INT_MIN, 0, mid_res);
return res;
}
void backTrack(vector<int>& nums, int last, int cur, vector<int>& mid_res) {
if (cur == nums.size()) {
if (mid_res.size() >= 2) {
res.push_back(mid_res);
}
return;
}
// 选择cur位置的元素
// nums[cur] >= last保证结果是递增
if (nums[cur] >= last) {
mid_res.push_back(nums[cur]);
backTrack(nums, nums[cur], cur + 1, mid_res);
mid_res.pop_back();
}
// 不选择cur位置的元素
// 这里判断nums[cur] != last为了去重
if (nums[cur] != last) {
backTrack(nums, last, cur + 1, mid_res);
}
}
};这个递归版本很容易就能写出来了,每个位置元素取正反即可
class Solution {
public:
int res;
int findTargetSumWays(vector<int>& nums, int target) {
dfs(nums, target, 0);
return res;
}
void dfs(vector<int>& nums, int target, int cur) {
if (cur == nums.size()) {
if (target == 0) {
res++;
}
return;
}
dfs(nums, target - nums[cur], cur + 1);
dfs(nums, target + nums[cur], cur + 1);
}
};但是这一题是典型的0-1背包问题,用上述的回溯方法会导致复杂度很高,达到指数级别O(2^N),如果采用背包问题的DP解法,会大幅度降低时间复杂度。
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
// 求和
int sum = 0;
for (int& num : nums) {
sum += num;
}
// 如果diff小于0,则说明没有满足的负数和
int diff = sum - target;
if (diff < 0 || diff % 2 != 0) {
return 0;
}
int n = nums.size(), neg = diff / 2;
// dp
vector<vector<int>> dp(n + 1, vector<int>(neg + 1));
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
int num = nums[i - 1];
for (int j = 0; j <= neg; j++) {
dp[i][j] = dp[i - 1][j];
// 如果j大于当前num,则可以取当前num的结果
if (j >= num) {
dp[i][j] += dp[i - 1][j - num];
}
}
}
return dp[n][neg];
}
};当然可以继续对二维DP数组进行优化,可以发现dp[i][j]只与dp[i-1][]有关,所以可以省去第一维,但是要注意dp更新时的遍历方向
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for (int& num : nums) {
sum += num;
}
int diff = sum - target;
if (diff < 0 || diff % 2 != 0) {
return 0;
}
int neg = diff / 2;
vector<int> dp(neg + 1);
dp[0] = 1;
for (int& num : nums) {
// 注意这里要反向遍历,保证转移来的是dp[i−1][]中的元素值
for (int j = neg; j >= num; j--) {
dp[j] += dp[j - num];
}
}
return dp[neg];
}
};上面提到了0-1背包问题,那么就不得不提到我们常用的解题方法,动态规划DP了。
动态规划一般分为几步:
- 建立dp数组
- 考虑边界条件初始化
- 状态转移方程
- 更新dp数组
- 得出最终结果
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
if (n < 2) {
return s;
}
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i..j] 是否是回文串
vector<vector<int>> dp(n, vector<int>(n));
// 初始化:所有长度为 1 的子串都是回文串
for (int i = 0; i < n; i++) {
dp[i][i] = true;
}
// 递推开始
// 先枚举子串长度
for (int L = 2; L <= n; L++) {
// 枚举左边界,左边界的上限设置可以宽松一些
for (int i = 0; i < n; i++) {
// 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得
int j = L + i - 1;
// 如果右边界越界,就可以退出当前循环
if (j >= n) {
break;
}
if (s[i] != s[j]) {
dp[i][j] = false;
} else {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substr(begin, maxLen);
}
};另一版超级简洁的
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
vector<vector<int>> dp(n, vector<int>(n));
string ans;
for (int l = 0; l < n; ++l) {
for (int i = 0; i + l < n; ++i) {
int j = i + l;
if (l == 0) {
dp[i][j] = 1;
} else if (l == 1) {
dp[i][j] = (s[i] == s[j]);
} else {
dp[i][j] = (s[i] == s[j] && dp[i + 1][j - 1]);
}
if (dp[i][j] && l + 1 > ans.size()) {
ans = s.substr(i, l + 1);
}
}
}
return ans;
}
};正则表达式匹配
这题的边界情况十分复杂,可以查看这个题解进行详细了解,需要注意的是,从后往前比较会好理解一些。
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size();
int n = p.size();
// dp[i][j]表示s[0:i-1]与p[0:j-1]是否匹配
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
// 初始化
dp[0][0] = true;
// 如果i为0,考虑p[j-1]是否等于*,若不等,则false,若等,则可以去掉p最后两个字符,继续判断dp[0][j-2]
for (int j = 1; j <= n; j++) {
if (p[j - 1] == '*')
dp[0][j] = dp[0][j - 2];
}
// 循环更新dp
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// 情况1:如果s[i-1]和p[j-1]匹配
if (s[i - 1] == p[j - 1] || p[j - 1] == '.')
dp[i][j] = dp[i - 1][j - 1];
// 情况2:如果s[i-1]和p[j-1]不匹配,分两种情况
else {
// 情况2.1:p[j-1]为*,分两种情况
if (p[j - 1] == '*') {
// 情况2.1.1:s[i-1]匹配p[j-2]
if (s[i - 1] == p[j - 2] || p[j - 2] == '.') {
// *重复0次或者1次或者2次以上
dp[i][j] = dp[i][j - 2] || dp[i - 1][j - 2] || dp[i - 1][j];
}
// 情况2.1.2:s[i-1]不匹配p[j-2],可以认为*重复0次,继续判断
else {
dp[i][j] = dp[i][j - 2];
}
}
// 情况2.2:s[i-1]不等于p[j-1]
else
dp[i][j] = false;
}
}
}
return dp[m][n];
}
};通配符匹配
这题与上题类似,但考虑的情况没有那么多,?必须匹配一个字符(不能匹配空字符),*可以匹配任意个字符(包括空字符):
- 当遇到?时,直接令dp[i][j] = dp[i-1][j-1]
- 遇到*时,可认为其代表空字符,即dp[i][j] = dp[i][j-1];也可认为其代表任意个字符,这时消除s的最后一个字符,同时保留*,即dp[i][j] = dp[i-1][j]
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size();
int n = p.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1)); // 初始化默认均为false
dp[0][0] = true;
// 当p前j个字符均为*时,才能匹配上s0
for (int i = 1; i <= n; i++) {
if (p[i - 1] == '*') {
dp[0][i] = true;
}
else {
break;
}
}
// 遍历m和n
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (p[j - 1] == '*') {
dp[i][j] = dp[i][j - 1] | dp[i - 1][j];
}
else if (s[i - 1] == p[j - 1] || p[j - 1] == '?'){
dp[i][j] = dp[i - 1][j - 1];
}
}
}
return dp[m][n];
}
};接雨水
这题上面有单调栈的做法很好理解,dp的话是针对于暴力解法的一种优化,leftmax和rightmax用于保存i及其左右范围内的最大高度
class Solution {
public:
int trap(vector<int>& height) {
int n = height.size();
if (n <= 2) return 0;
int res = 0;
vector<int> leftmax(n);
leftmax[0] = height[0];
for (int i = 1; i < n; i++) {
leftmax[i] = max(leftmax[i - 1], height[i]);
}
vector<int> rightmax(n);
rightmax[n - 1] = height[n - 1];
for (int i = n - 2; i >= 0; i--) {
rightmax[i] = max(rightmax[i + 1], height[i]);
}
for (int i = 0; i < n; i++) {
res += min(leftmax[i], rightmax[i]) - height[i];
}
return res;
}
};- 贪心 这题是典型的贪心算法题,从后往前找能到达指定位置的最远点即可,但这样的时间复杂度是o(n^2),从前往后则是O(n),但是需要注意不能只考虑一步,需要考虑两步才能保证贪心找到的点是能达到最远距离的。
class Solution {
public:
int jump(vector<int>& nums)
{
int max_far = 0;// 目前能跳到的最远位置
int step = 0; // 跳跃次数
int end = 0; // 上次跳跃可达范围右边界(下次的最右起跳点)
for (int i = 0; i < nums.size() - 1; i++)
{
max_far = std::max(max_far, i + nums[i]);
// 到达上次跳跃能到达的右边界了
if (i == end)
{
end = max_far; // 目前能跳到的最远位置变成了下次起跳位置的有边界
step++; // 进入下一次跳跃
}
}
return step;
}
};- dp 这题同样能用dp去做,设定dp[i]代表移动到位置i,需要的最少步骤数 可以想到:当前位置i,由上一位置j向右移动最多nums[j]而得到(可能不需要移动nums[j]就到了位置i) 那么就可以列出状态转移方程: dp[i] = min(dp[i], dp[j] + 1)
class Solution {
public:
int jump(vector<int>& nums) {
// dp代表到达i位置所需的最小跳跃次数
vector<int> dp(nums.size(), INT_MAX);
dp[0] = 0;
for (int i = 1; i < nums.size(); i++) {
for (int j = 0; j < i; j++) {
// 当j + nums[j] >= i说明j可以跳到i,此时更新dp
if (j + nums[j] >= i) {
dp[i] = min(dp[j] + 1, dp[i]);
}
}
}
return dp[nums.size() - 1];
}
};此种写法复杂度为O(n^2)
- 贪心
与上题基本类似,维护一个能到达的最远距离,如果大于数组最后一位,则返回true,如果当前遍历位置大于能到达的最远距离,返回false
class Solution {
public:
bool canJump(vector<int>& nums) {
int max_pos = 0;
for (int i = 0; i < nums.size(); i++) {
if (i > max_pos) return false;
max_pos = max(max_pos, nums[i] + i);
}
return true;
}
};- dp
与上一题类似,复杂度较高,不推荐了
这题可太经典了,典型的dp题,dp[i][j]表示到达i,j位置可能存在的路径数,因为只能向右向下走,所以dp[i][j] = dp[i-1][j] + dp[i][j-1]
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n));
// 初始化
for (int i = 0; i < m; i++)
dp[i][0] = 1;
for (int j = 0; j < n; j++)
dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};因为dp[i][j] = dp[i-1][j] + dp[i][j-1]只与左边和上面有关系,因此可以压缩dp至一维
class Solution {
public:
int uniquePaths(int m, int n) {
// 可以压缩dp[i][j]为dp[i] ,因为dp[i][j]只与dp[i-1][j]和dp[i][j-1]有关
// dp[i]可以表示第i列的路径数量
// 然后从左往右,从上往下遍历,可以将dp[i][j] = dp[i-1][j]+dp[i][j-1]
// 表示为dp[j] = dp[j] + dp[j - 1],这里的dp[j-1]是新一行的,dp[j]是上一行的
vector<int> dp(n+1, 1);
for (int i = 2; i <= m; i++) {
for (int j = 2; j <= n; j++) {
dp[j] = dp[j] + dp[j - 1];
}
}
return dp[n];
}
};这题多了个障碍物,在状态转移的时候需要考虑多一点了,dp[i][j]表示到达i,j位置可能存在的路径数,如果i,j处是障碍物,则dp[i][j]=0
class Solution {
public:
// 动态规划
// dp[i][j]表示到i,j点可能的所有路径数
// dp[i][j] = dp[i-1][j] + dp[i][j-1] dp[i][j]只可能是从左和上来的,因此是两点可能路径之和
// 考虑初始条件,第一列只可能是从上来的,因此为1(该点为障碍物是为0)
// 同样,第一行只可能是从左来的,因此为1(该点为障碍物是为0)
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
dp[0][j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 0) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
}
return dp[m - 1][n - 1];
}
};最小路径和
与上一题类似,需要多考虑的一步是取两条路径中的小的一条作为路径和
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<vector<int>> dp (m, vector<int>(n));
dp[0][0] = grid[0][0];
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
for (int j = 1; j < n; j++) {
dp[0][j] = dp[0][j - 1] + grid[0][j];
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
return dp[m - 1][n - 1];
}
};三角形的最小路径和
这题与上面也是思路一模一样,需要多考虑一个最下面一行的路径只能从左上角而来
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
int n = triangle.size();
vector<vector<int>> f(n, vector<int>(n));
f[0][0] = triangle[0][0];
for (int i = 1; i < n; ++i) {
f[i][0] = f[i - 1][0] + triangle[i][0];
for (int j = 1; j < i; ++j) {
f[i][j] = min(f[i - 1][j - 1], f[i - 1][j]) + triangle[i][j];
}
f[i][i] = f[i - 1][i - 1] + triangle[i][i];
}
return *min_element(f[n - 1].begin(), f[n - 1].end());
}
};编辑距离
class Solution {
public:
int minDistance(string word1, string word2) {
int m = word1.size();
int n = word2.size();
// dp[i][j]代表word1[:i]与word2[:j]的编辑距离
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
// 初始化
for (int i = 0; i <= m; i++) {
dp[i][0] = i;
}
for (int i = 0; i <= n; i++) {
dp[0][i] = i;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = min(min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), dp[i - 1][j - 1] + int(word1[i - 1] != word2[j - 1]));
}
}
return dp[m][n];
}
};//严蔚敏《数据结构》标准分割函数
Paritition1(int A[], int low, int high) {
int pivot = A[low];
while (low < high) {
while (low < high && A[high] >= pivot) {
--high;
}
A[low] = A[high];
while (low < high && A[low] <= pivot) {
++low;
}
A[high] = A[low];
}
A[low] = pivot;
return low;
}
void QuickSort(int A[], int low, int high) //快排母函数
{
if (low < high) {
int pivot = Paritition1(A, low, high);
QuickSort(A, low, pivot - 1);
QuickSort(A, pivot + 1, high);
}
}当遇到相关联的东西放到一起的时候,就需要用到并查集。
并查集是用来将相同的元素集合到一起的算法,设置f数组存储各元素的集合头目,实现find寻找头目,isconnected判断两个元素是否在一个集合内,merge合并两个集合。
代码如下:
class UnionFind {
private:
vector<int> f;
int count;
public:
UnionFind(int count) {
this.count = count;
f.resize(count);
for (int i = 0; i < count; i++) {
f[i] = i;
}
}
int find(int p) {
assert( p >= 0 && p < count );
while( p != f[p] )
p = f[p];
return p;
}
bool isconnected(int p, int q) {
return find(p) == find(q);
}
void merge(int p, int q) {
int rootp = find(p);
int rootq = find(q);
if (rootp == rootq)
return;
f[rootp] = rootq;
}
}class Solution {
public:
vector<int> f;
int find(int x) {
return f[x] == x ? x : f[x] = find(f[x]);
}
bool check(const string &a, const string &b, int len) {
int num = 0;
for (int i = 0; i < len; i++) {
if (a[i] != b[i]) {
num++;
if (num > 2) {
return false;
}
}
}
return true;
}
int numSimilarGroups(vector<string> &strs) {
int n = strs.size();
int m = strs[0].length();
f.resize(n);
for (int i = 0; i < n; i++) {
f[i] = i;
}
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int fi = find(i), fj = find(j);
if (fi == fj) {
continue;
}
if (check(strs[i], strs[j], m)) {
f[fi] = fj;
}
}
}
int ret = 0;
for (int i = 0; i < n; i++) {
if (f[i] == i) {
ret++;
}
}
return ret;
}
};- K 个一组翻转链表
这题就是依次倒转各个部分,然后返回倒转后的头尾,并跟原数组的其他部分连接起来。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
// 翻转子链的函数
pair<ListNode*, ListNode*> myReverse(ListNode* head, ListNode* tail) {
// 初始化pre为尾部后一个是为了第一次操作时把头变成尾再指向原链表
ListNode* pre = tail->next;
// now表示当前正执行操作的指针
ListNode* now = head;
while (pre != tail) {
// nex表示now的后一个
ListNode* nex = now->next;
// 把now指向前一个指针
now->next = pre;
// 前一个指针变成now
pre = now;
// now指向下一个指针
now = nex;
}
return {tail, head};
}
ListNode* reverseKGroup(ListNode* head, int k) {
ListNode* start = new ListNode(0);
start->next = head;
ListNode* pre = start;
while(head) {
ListNode* tail = pre;
// tail变到从head开始第K个位置
for (int i = 0; i < k; i++) {
tail = tail->next;
if (!tail) {
return start->next;
}
}
// nex表示尾部后面一个
ListNode* nex = tail->next;
// 对head到tail之间的子链进行翻转,返回新的头尾指针
pair<ListNode*, ListNode*> res = myReverse(head, tail);
head = res.first;
tail = res.second;
// 连接原链表与翻转后的子链
pre->next = head;
tail->next = nex;
// 进行新一轮翻转的pre和head设置
pre = tail;
head = tail->next;
}
return start->next;
}
};