SysY_Compiler设计文档

一、参考编译器介绍

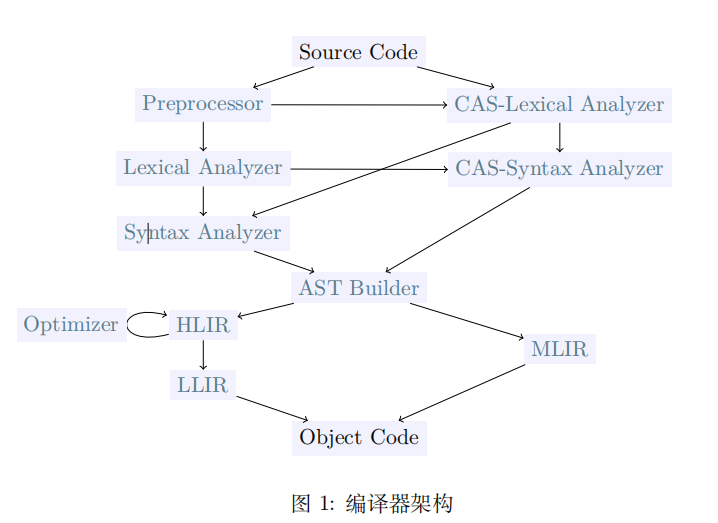
在这个学期中，我参考的编译器为19级学长的编译器。

学长的编译器实现了非常好的解耦合，词法分析、语法分析、语义分析、优化、代码生成几个模块之间的界限十分清晰，不同模块之间的信息传递仅有前面模块传处理后的结果给后一个模块，除此之外，各个模块之间没有任何的信息交换。

二、编译器总体设计

我将编译器实现了解耦，每一个模块负责相应的功能实现，分别为：词法分析、语法分析、语义分析、优化、代码生成。

不同的模块之间不存在相互调用，不同模块之间的联系仅为模块处理结果的传递。

词法分析模块会将源程序转变为tokenlist，并将其提供给语法分析模块； 语法分析模块会进行错误分析、语法树的建立、符号表的建立，并将其提供给语义分析模块； 语义分析模块会生成四元式列表，将其提供给优化器； 优化器优化完四元式（中间代码）后，将其提供给代码生成器； 代码生成器生成最终的 MIPS代码。

public static void main(String[] args) {
    // 词法分析器
    LexicalAnalyser lexicalAnalyser = new LexicalAnalyser();
    lexicalAnalyser.startLexicalAnalyse();

    // 语法分析
    Parser parser = new Parser(lexicalAnalyser.getTokenDateList());
    parser.startToParse();

    // 语义分析与中间代码生成
    TetradGenerator tetradGenerator = new TetradGenerator(
        parser.getTreeRoot(), parser.getBaseSymbolTable()
    );
    tetradGenerator.startToGen();

    // 输出优化前的代码
    MidCodePrinter midCodePrinter1 = new MidCodePrinter(
        tetradGenerator.getTetradList(),
        tetradGenerator.getStrToPrintList(),
        "testfilei_20373921_丁盛为_优化前中间代码.txt"
    );
    midCodePrinter1.start();

    // 代码优化
    Optimizer optimizer = new Optimizer(
        tetradGenerator.getTetradList(),
        tetradGenerator.getStrToPrintList());

    // 输出优化后的代码
    MidCodePrinter midCodePrinter2 = new MidCodePrinter(
        optimizer.getTetradList(),
        optimizer.getStrToPrintList(),
        "testfilei_20373921_丁盛为_优化后目标代码.txt"
    );
    midCodePrinter2.start();

    // 目标代码生成
    MipsGenerator mipsGenerator = new MipsGenerator(optimizer.getTetradList(), optimizer.getStrToPrintList());
    mipsGenerator.startToGenMIPS();
}

我的项目结构如下

─src
    │  Compiler.java			主类，项目入口
    │
    ├─constDecl
    │      LexicalConst.java	词法分析中的常量
    │      NodeConst.java		语法树节点中的常量
    │      SymbolConst.java		符号类的常量
    │
    ├─errorHandler				
    │      ErrorDate.java		表示错误信息的类
    │      ErrorHandler.java	错误处理器
    │
    ├─lexical
    │      LexicalAnalyser.java	词法分析器
    │      TokenDate.java		表示Token的类
    │
    ├─mipsGenerator
    │      MipsGenerator.java		中间代码生成器
    │      MipsGeneratorTool.java	中间代码生成时用到的工具
    │      Reg.java					存储寄存器的常量
    │      RunTimeStack.java		运行栈
    │      StackItem.java			运行栈中信息
    │
    ├─optimizer
    │      MidCodePrinter.java		四元式转中间代码
    │      Optimizer.java			优化器
    │
    ├─parser
    │      Parser.java			文法分析器
    │      ParserTools.java		文法分析工具
    │      TreeNode.java		语法树节点
    │
    ├─symbolTable
    │      Symbol.java			符号表中符号
    │      SymbolTable.java		符号表
    │
    └─tetradGenerator
            Message.java			属性翻译文法中的信息
            Tetrad.java				四元式
            TetradGenerator.java	四元式生成器

三、词法分析设计

目标及总体设计

**目标：**对文法进行分析，记录单词的类别和单词值。

总体设计：

• 在读到源代码末尾之前，一直调用getSym()读取单词，并将读取到的单词存入TokenDataList中。
• 对于getSym()：用于获取新的token，一个个的读取字符同时跳过空白符，依照文法对新字符进行处理：第一个字符决定的此token后续对字符的文法约束。对于后来获得的字符，若符合文法，将其拼在字符串后面；若不符合文法（常常是空白符或运算符），将现有的字符串分类记录并return。
• TokenDate：新建一个TokenData类用于存储每个token的信息，如：name（源代码中的字符串）、category（对应的类别）、lineNum（行号）、value（若是数字，记录int值）

设计细节

一些约定和函数： char nowChar：来表示此时待处理的字符 int lineNum：记录行号 void getChar()：刷新nowChar为下一个待处理的字符 void getSym()：获取下一个token。约定在调用getSym()时，nowChar为将要分析的哪个字符

有关读入和行号的记录： 词法分析中仅采用gatChar()进行读入，有关读入的全部信息都被封装在其中。 运行逻辑：使用scanner.nextline()从testfile.txt中读入一个新String，调用getChar()时就获取当前char的后一个char。当读到行尾时，将nowChar置为\n。当nowChar == '\n'时调用getChar()，会读入新行并lineNum++。

有关输出： 全部分析完成后，按顺序输出TokenDataList中的信息。

完成代码后的修改

本次设计较为成功，没有进行设计上的修改

四、语法分析设计

目标及总体设计

**目标：**按照文法要求输出语法分析结果，得到一棵符合原始文法的语法树

**总体设计：**使用梯度下降的方法进行语法分析

主要挑战及解决方式

挑战1

语法分析的难点来自于“左递归文法”和对输出顺序的要求。左递归文法与递归下降是天然矛盾的，这可以通过修改文法解决，但是如果修改文法，就会导致最后得到的语法树不符合原文法。

**解决：**观察文法可知，左递归文法主要出现在表达式部分，而且形式都比较简单，都是addExp -> addExp + mulExp | mulExp这一类。 我将其改为右递归文法进行分析，然后修改的树的结构，使其符合原始文法，以前面的产生式为例，具体parseAddExp()的操作如下：

1. 首先建立nowNode = newNode(addExp)，同时parseMulExp()得到childNode，接着nowNode.addChild(childNode)。
2. 然后while(是不是+)，如果是+，则接着分析，新定义一个newFaNode = newNode(addExp)，将此时的nowNode作为newFaNode的子节点。接下来parseMulExp()得到的节点作为newFaNode的新子节点。

直观的理解第2条，就是每遇到一个MulExp，都在当前的树节点上方新加一层，从而模拟出左递归时语法树的情况。还是比较巧妙的，不用很多的代码就解决了左递归的问题，同时得到了符合原文法的语法树。

挑战2

产生式右侧不同候选式的first集的交集不为空，这意味着要么采用回溯的写法，要么预读。

**解决：**采用偷瞄的方式解决这个问题，通过预读特定位置的token确定当前需要选择的产生式。

设计细节

一些定义和约定： getSym()：从词法分析的结果tokenDataList中取出一个新的Token。 注：词法分析器中也有一个getSym()，两者同名 调用parsexxx()时已经读入了一个token

关于error的判断： 此次作业中不涉及，但是我对可能出错的地方进行了判断。判error的条件为“终结符不匹配”，只有在终结符“直接不匹配”时才报错。若一个文法右侧不存在终结符，就不需要报错。 举例：A->B B->'int'，在parseA()中，即便知道此时的sym不是int，也不能报错，因为A右侧并没有直接出现int。parseA()只需要转入parseB()，在parseB()中发现终结符int不匹配，报错。

输出方法： 在parsexxxExp()return之前输出<xxxExp>。 在getSym()时输出token的信息

语法树中节点的信息： 一个指向token的指针（对于叶节点） 一个arraylist，指向子节点 一个childNum，表示arraylist的长度 and 子节点的个数 一个指向父节点的指针parent

完成代码后的修改

发现之前的设计存在冲突： 约定1“在parsexxx()时已经读入了一个token” 跟 约定2“在parsexxxExp()return之前输出<xxxExp>，在getSym()时输出token的信息” 会导致最后的输出不符合条件，原因如下： 因为约定1的约束，在parsexxx()结束前需要添加一个getSym()，这样在parse嵌套时就无法得到期望的结果，例如在A->const B，B->int，在parseA()的最后需要写parseB()，而parseB()会在结束前进行getSym()，导致输出时非终结符<A>前多了一个无关的Token信息。

仔细观察输出格式，可发现输出结果恰好为语法树的后序遍历结果，因此我修改了输出方法：不在递归下降的过程中输出，而是在语法分析结束后，将“语法树的后序遍历结果”输出，解决了以上问题。

五、错误处理设计

符号表的设计

首先设计一个符号表，考虑到只需要从深层访问浅层的符号表，因此给符号表建立链接,使其可以找到自己的父符号表，同时标记其所处的深度(设置全局变量深度为0，主函数深度为1)。

定义全局变量nowTable表示当前的符号表，每当进入一个新的层时，就建立一个新的符号表，并将之前的符号表作为父表。当退出当前层时，就舍弃当前的符号表，将父表作为nowTable。

public class SymbolTable {
    private HashMap<String, Symbol> symbolMap;
    private int level;      // 当前符号表所处的层的深度
    private SymbolTable faTable;    // 上一层的符号表
    private int blockType;  // 分为NORMAL_BLOCK、LOOP_BLOCK、VOID_FUNC_BLOCK、INT_FUNC_BLOCK 四种
    private ErrorHandler errorHandler;  
    // 当前block中（不包括子层），上一句的stmt类型，有normal和return两种，用于int型函数最后一句的判定
    private int lastStmtType; 
}

对于数组，由于SysY中变量类型仅有int，且某一维下界必为0，因此需要记录的有关数组的信息并不多，所以并不单独设计数组信息记录表，直接将其嵌入符号表中。

对于函数，由于其需要进行参数个数和参数类型的检查，因此需要记录参数的信息。由于变量类型只有int一种，因此类型检查主要关注的就是数组，需要区分一般变量、一维数组、二维数组，且一维数组第一维的长度缺省，二维数组需要记录第二维的大小。因此可以建立了一个列表，使用其记录参数的信息，-1表示为普通变量，-2表示为一维数组，用非负数表示二维数组第二维的长度。

综上，对于符号，根据错误处理有关的信息，设置相关属性：

public class Symbol {
    private String name;
    private int lineNum;    // 声明symbol时的行号
    private int type;   // 标记CONST, VAR, PARAM, VOIDFUNC, INTFUNC
    private int dim;    // 主要是为了数组，一般变量和函数就是0，数组则会是1，2
    private String address;	// 暂时没有用上
    // 仅数组有用记录数组元素某一维的上界，(这个事留到语义分析做)
    private ArrayList<Integer> arrayUpBoundList;
    // 仅函数时有用，记录参数的维度，为0，1，2
    private ArrayList<Integer> paraDimList; // 列表的len就代表了参数的个数
    private int paraNum;

变量增加与查询

在定义相关语句中将变量加到当前的符号表中，同时检查在当前层的符号表中是否有名字重定义的情况出现。

有关循环体

定义全局变量loopLevel=0，其会记录当前所处的循环深度，为0表示不在循环体中，每进入循环就自增，退出循环就自减。

函数设计

在符号表设计时就已经考虑了函数相关的情况，符号表中记录了函数参数的各种信息，可以用于进行数量匹配以及类型匹配的检查。在“符号表设计”一节中已经分析过了，参数类型匹配只需检查维数是否匹配，实际操作的细节如下：

• **形参的存储：**值得注意的是函数名需要放在上层的符号表中，形参需要放在下层的符号表中，但是在符号表中需要根据函数名获取参数的信息。因此在进行函数定义时，要分析完函数名和参数之后，才将他们统一填入符号表中，并建立下一层的符号表。
  • 在函数名的symbol中，仅需要存储每一个参数的类型就可以了，不关系参数的名字。因此引入一个列表，使用其记录参数的信息，使用0，1，2来表示普通变量、一维、二维数组。 （也可以选择保留更多的信息例如：-1表示为普通变量，-2表示为一维数组，用非负数表示二维数组第二维的长度，但这样其实就引入了计算，例如：a[][2+3]，在错误处理阶段并不想设计的太过复杂，因此选用第一种方法）
• **实参的匹配：**从左往右进行匹配，根据文法的要求，当出现不匹配时就报错，当匹配到最后一位时，进行匹配个数的检查。这一部分的难点为Exp的种类多样，难以确定实际的个数以及参数类型，尤其是函数嵌套的情况难以处理。
  • 参数类型的确定：即参数维数的确定。难点在于分析时不知道到底是要将哪一个变量作为参数进行传递，例如一个Number可以是参数，但ident[Number]中的Number就不是参数。考虑到语法树的存在，无论当前的Exp有多么复杂，梯度下降到最后一定会回到FuncRParams → Exp { ',' Exp }右侧的Exp，因此可以考虑维护一个值来表示最新的元素的维数，不妨设其为AType，每当分析到Exp及可由其推出的量时，更新AType即可，最后得到的AType就是FuncRParams → Exp { ',' Exp }右侧的Exp的维数。
  • 关于函数的嵌套：一个函数的参数有可能时另一个函数的返回值，例如：f(1, g(2))，因此分析函数参数时，需要保证对每一个函数的分析都是独立的。在设计时，我定义了一个全局栈funcRealParaTopStack，栈内的每一个元素都是栈realParaStack(采用链表模拟实现)，用于分析不同函数的参数，记录它们的维数，realParaStack中的元素就上上一条中的AType。在需要增加栈元素时，手动在栈顶加入一个元素，其他情况中，每需要更新栈顶元素时，需要先弹栈再入栈，以此控制栈中元素的数量。
  • 为什么要使用栈来记录某一个函数的实参信息？ 有两个原因，一是通过引入一个栈，可以将判断参数是否匹配的工作放在parseUnaryExp中，这样就可以直接获取函数名的行号，省的保存。二是对于mul + mul的情况，可以自己手动增加元素，将每一mul的维度都保存下来，可以用于检查加法两侧元素类型是否相同，作业中用不到。

返回值检查

函数存在两种不同的类型，为了区分，设置一个全局变量curFuncType 来表示当前所处函数的类型是void还是int。

1. void类型的函数 每遇到return 时就检查函数类型以及是否存在返回值。需要注意的是有可能出现不含分号的错误，即仅有return没有Exp和 ;。

2. int类型的函数 其是在遇到函数末尾的} 时进行报错，有两种方法解决问题：1是每遇到一个return，就预读后方是否存在}，其难点在于这样做需要特别关注return语句是否在函数末尾。2是引入一个全局标记，记录上一个stmt语句的类型（NotReturnStmt、VoidReturnStmt、IntReturnStmt），在遇到函数末尾的} 时通过查找标记决定是否正确。

   • 如何确定当前是不是处于函数末尾？

     与循环体中break的判断不同，那个只需要判断在不在循环体中，因此一个全局变量就可以完成记录。 与void函数的return也不同，那个需要对每一个return都进行判断，因此遇到一个处理一个就行了。

     此处需要判断是不是函数块的最后一个语句，需要采用特殊的方法： 由于函数定义一定会引入Block，即一定会引入{}，一定会增加新的符号表层，因此可以给符号表设标记blockType，标记为voidFuncBlock、intFuncBlock、norbalBlock。每当遇到}时就检查函数类型以及符号表中的标记，如果为intFunc且 当前符号表中blockType为intFuncType(说明到了函数后面第一个block的末尾)，就进行检查。

可能出现的bug

• 默认while循环之后的那个stmt一定是block，： 'while' '(' Cond ')' Stmt。 因为需要通过block来明确loop的层。 可能影响m的报错。

完成错误处理后对原设计的修改

有关函数

在写代码时一下没想清楚函数的定义与函数的调用：函数的调用可能出现函数的嵌套，但是函数的定义不会出现，因此可以仅使用一个全局变量nowDeclFuncType标记此时所处的类型，原设计其实可行，而且相比我最后的版本还简单不少。

由于当时没想清楚，考虑到函数的定义一定有一个对应的block，因此我选择在符号表中打标记，如果当前符号表所对应的block为函数定义产生式中右侧的那个block，对其进行标记。当需要判断当前是不是处于一个函数中时，可以向上遍历符号表的标记。

函数实参

由于一行只会有一个错误，因此在调用函数时，如果实参中出现未定义的变量，那么需要报未定义的错误，此时无需考虑函数参数类型不匹配的问题。 为了实现这一点，在检测到未定义的变量时，引入一个“万能匹配”标记，表示在进行参数维度匹配时，可以将其忽略。

当void函数作为函数实参时，一定要报错，因此引入一个“错误匹配”标记，其一定会引起实参类型不匹配的错误。

函数返回值

对于int类型的函数，只需判断最后一天语句中存不存在return，没有要求要是return exp，因此将VoidReturnStmt、IntReturnStmt合并为一个returnStmt。

循环深度的记录

在实现错误处理时发现我对梯度下降的理解不够深入：对于stmt->'while' '(' Cond ')' Stmt时，仅需要在stmt->'while' '(' Cond ')' @plusLevel Stmt @minusLevel就可以完美实现对循环深度的记录。

实现时想复杂了，选择设置一个全局变量，表示下一个block的种类，然后再parseBlock中实现循环深度的更新。伪代码如下：

private void parseBlock() {
    if (新block是循环block) {
        标记nowSymTableType = LoopBlock;
        loopLevel++;
    }
    ...
    if (nowSymTableType == LoopBlock)
        loopLevel--;
}

这样有bug，因为whle后并不一定有block，此时会出错。但我写了那么多不想改了，都是心血，最后特判当下一个stmt不是block时，使用第一段中提到的方法更新loopLevel。

可能的bug

难点在于return时区分LVal和exp。

对于return [exp];的情况，考虑到分号有可能确实，同时$First(exp) \cap First(LVal) = {ident} \neq \phi$，同时由于;可能缺失，因此当下一个token为ident时，必须精确判断return后的语法树为exp还是LVal = ...。此时考虑到了题目中说到的没有恶意换行，因此决定使用以下方式判断：向后预读，先换行 或者 预读到;，认为为exp，先预读到=说明为LVal = ...。

以上做法在遇到如下情况时会出错：

return exp Lval = ...;	// return exp缺少分号，同时下一句LVal没有换行

return
Lval = ...;		// 预读时先遇到换行，会parseExp，出错

六、语义分析 和 代码生成设计

宏观设计

代码生成核心分为两步： 第一步是分析语法树获取四元组，第二步是将自己设计的四元组翻译为mips。即不会进行翻译为中间代码的操作 获取四元组将文法改写为属性翻译制导文法，然后使用递归下降进行分析，最后的获得一个四元式列表。

我的设计并不包含中间代码，MIPS是直接基于四元式生成的。在生成MIPS时，唯一的信息来源就是四元式，因此在宏观的设计上，在四元式生成阶段将尽可能多的信息都处理了，使得四元式中的信息都足够简单、底层。 例如：在四元式生成阶段为所有的变量提供唯一标识，这样MIPS生成时就无需考虑重名的信息。 在四元式中不存在“二维数组”的概念，数组都是一维的，存取都靠偏移，因此数组的存取需要专门使用四元式计算出offset，然后采用arrayName+offset的方式实现存取。

因为需要确保四元式中的信息尽可能地简单，在生成四元式阶段有如下的一些约定：

• 四元式中不存在重名变量
• 四元式中只有一维数组的概念，通过基地址和偏移量来进行定位
• 四元式中不存在if，while等语句的信息，有关分支的信息全部转为 label + 跳转(bnez,j等)来实现。 也因此四元式中不存在对一元运算符!的操作，其转为了类似if-else的形式实现
• 四元式中main函数被视为普通的函数，为此我人为设计了一个新层，其会实现 对全局变量的赋值、跳转到main函数、main函数结束后退出程序 3个功能。
• 四元式中不会出现对const变量的读写，在四元式生成阶段就将全部const转为数字
• 代码生成阶段什么优化都不做，大量引入中间变量来暂存结果，全部的变量都放在栈上

四元式设计

public enum OpType {    // 表示操作的类型
    // 计算相关
    assign,         			// (op, label1, _ ,des)
    add, sub, mul, div, mod,	// (op, var1, var2, des)  var1和var2中可以有一个是常量
    
    // 一元表达式
    unaryOp_add,  unaryOp_sub,   // (op, label1, _, des)
    // unaryOp_not  不存在!的四元式，因为其涉及到了if-else，而label相关的信息我是在四元式中就确定了的，因此直接使用if-else的方法处理完了

    // 定义一般变量
    defVar_normal,                // (op, _, _, var)
    defVar_normal_AndAssign,      // (op, label, _, var)
    defConst_normal_And_Assign,   // (op, num, _, var)需要与数组进行区分(const的定义一定是会进行赋值的)

    // 数组相关的内容
    defOneDimArray,     // (op, size, _, array)
    defTwoDimArray,     // (op, size1, size2, array) 实际上定义1，2维数组可以合并成一个defArray，只需要数组名和数组大小两个信息
    defFuncPara_oneDim, // (op, _, _, var)    定义一维数组，长度缺省	实际上函数中数组形参的定义可以合为一个，因为无需数组大小的信息
    defFuncPara_twoDim, // (op, size, _, var) 定义二维数组，第1维长度缺省，第二维需要指明大小。实际上size这个信息是多余的
    getArrayVal,        // (op, array, offset, des)  取出数组对应位置的值，并存到des中
    getArrayAddr,       // (op, array, offset, des)  计算数组对应的地址，并存到des中
    assignArrayVal,     // (op, offset, val, array)

    // 定义函数
    defFunc,    		// (op, _, _, funcName)
    defFuncPara_normal, // (op, _, _, var)

    // 调用函数
    pushPara,   // (op, index, _, var)	index表示这是第几个para，有了index以后可以十分方便的确定运行栈上的偏移量
    callFunc,   // (op, 参数个数, _, funcName)

    // return
    returnVoid,     // (op, _, _, _)
    returnInt,      // (op, _, _, ret)

    // 输入输出
    printStr,       	// (op, _, _, strLabel)
    printInt, getint,   // (op, _, _, ident)

    // 跳转 和 生成label
    bnez, beqz, bltz, blez, bgtz, bgez,     // (op, var, _, label)
    jump, genLabel         					// (op, _, _, label)
}

为变量名添加唯一标识

命名约定：

对于FUNC，其只会存在于baseRunTable中，为其加前缀 f_ 对于全局的CONST、VAR，为其加前缀 g_，MIPS生成时放在.data段中。 对于局部的CONST、VAR、PARAM，考虑到其名称可能以g_、f_为前缀而导致冲突，因此为其加前缀^,例如a->^a。若出现重名，则不断在其后面加^直至标识唯一 对于对于输出的字符串，统一命名为str_x，全部放在.data段 对于四元式分析过程中引入的temp变量，设置其命名为tx，如：t1,t2，显然其与以上所有变量命名之间一定互斥

根据以上设计，可以保证为所有的变量添加唯一标识

确定变量实体：

既然要为变量添加唯一标识，显然就需要找到某个变量对应的实体，例如int a = a;，等号右边的a对应的是之前的定义的某个变量，等号左边的变量则是刚定义出的一个新的变量实体。

之前错误分析阶段仅仅只做了重名与否的判断，无法区分某个变量名实际对应的变量实体，因此在符号表中引入boolean isAlive字段，其标记某个变量此时的“活性”。默认将其设为false，只有当定义之后将其置为true，此时从当前符号表开始向上找，找到的第一个isAlive = true的符合条件的symbol就是identName对应的变量实体。

数组相关设计

为了设计的简单，我强制使用一个变量来存储变量的基地址，寻址过程也变为首先访问这个基地址，然后加上偏移量得到实际地址，最后根据实际地址访问数组元素。

举例： int a[20];，首先会在运行栈上分配$204=80Byte$的空间来存储数组，然后再分配4Byte的空间存储数组的基地址（即那80Byte空间的最低地址），并将其设为数组的唯一标识（假设为^a）对应的空间。 当访存时，例如:b=a[10];，会先访存^a获取数组基地址baseAddr，然后加上偏移得到$realAddr = baseAddr + offset4$，将其存到某个寄存器后(例如：t0)，最后使用lw $t1, ($t0)实现访存。

这样子牺牲了一定的性能，多使用的一定的空间，但是简化了整体的设计，使得数组的访存方式得到统一，个人认为是可行的设计。

信息传递设计

在进行语法制导的翻译时，涉及到了信息的传递，因此新建Class Message来实现这一功能，其中Message的种类有：

public enum MesKind {
    ident_normal,  		// 非数组变量ident
    ident_and_offset,   // mes里面存ident，offset里面存offset。仅仅用于数组作为真正的左值要刷新值的时候使用
    temp,   			// 临时变量t_x
    num					// 传递的是一个常数
}

值得注意的是ident_and_offset仅仅用作数组作为“真正的”左值时才被使用，即a[i][j]=exp或a[i][j]=getint()时。对于数组的访存，会将访存的结果存到一个临时变量tx中，然后传递这个临时变量。函数的返回值也是如此，会用临时变量来封装。使用temp存值的方式大大的简化了设计，较少了message种类使得接收信息的一方无需针对信息的种类做很多的特判，大大提升了开发的效率。

细节设计

如何读取当前的符号表？

在进行数组的分析的时候，由于需要维度相关的信息，因此需要读取符号表，可以在parse那里，针对block类的node新增一项信息，用于查询到当前的符号表类型。 由于处理的是正确的程序，因此不必考虑变量重定义的问题，即使出现了变量覆盖的情况也是正常的，可以正确定位。

四元式转MIPS

总体框架

1. 完成.data段中所有全局变量的定义 计算出字符串的大小和位置，完成字符串的定义
2. 生成.text段： .text段一开始是自己设置的最顶层，其负责完成 对全局变量的赋值、跳转到main函数 和 退出控制台 这3个操作
3. 完成所有函数的MIPS生成（main函数也被视为一个普通的函数）

一些约定：

将mainFunc视为对一个普通函数的调用，因此在mainFunc放上还有一层代码，实现进入mianFunc 和 退出程序。

不考虑优化，暂时决定，所有有关参数的信息，都先放到栈上，不进行寄存器的分配。 因为无需进行寄存器的分配，因此运行栈中只需要存储 变量的名字 和 相对栈帧的偏移量 两个信息。

后期的修改

有关函数调用

在函数调用这一部分，我一开始的设计与设计思想“四元式中的信息都足够简单”矛盾。

**旧设计：**最终的四元式列表中，处理完一个实参就新增一个(pushPara, index, _,x)的四元式，然后再生成MIPS的时候，遇到pushPara的四元式之后，都将他们放到一个栈中，在遇到(callFunc, 参数个数, _, funcName)的四元式的时候才从栈中取出pushPara的有关信息执行pushPara的操作。

**旧设计的缺点：**1.与设计思想相违背； 2.不利于之后的优化，因为四元式列表中使用变量的位置跟目标代码中实际使用变量的位置不一致。

**新设计：**将这个“栈式”处理实参的过程前置到四元式生成阶段，在分析完所有的形参之后，直接生成所有的pushPara四元式，其后紧跟着callFunc。

**补充说明：**其实两种设计的四元式本身没有任何变化，变的是位置，新设计在效果和旧设计完全一致的基础上简化了生成MIPS的工作，同时方便了优化。之所以说“仅仅改变了四元式的位置”，是因为在我的设计框架中，所有的实参都要首先存到一个临时变量中，然后将这个临时变量作为实参进行传递，中间不涉及对此中间变量的读写。

有关信息传递

旧设计中，没有大量使用临时变量t_x进行变量值的存储，这就导致在进行属性翻译文法的分析的时候，需要对传递的信息进行很多特判。

新设计中，除了普通变量和常数信息，其它的变量统一暂存至一个临时变量中，然后传递信息时传递这个临时变量。

例如：旧设计中，存在信息为funcRet的message，那么在函数调用的上层，就要根据情况来特判。考虑如下情况：a=func1(func2(), func3())显然func2()的返回值需要暂存到一个临时变量中，但是a=func()中就不需要对返回值进行暂存处理。 旧设计的好处是可以得到一定的速度优势，坏处是可能引入大量的bug，极大的提高设计难度。考虑到旧设计所能取得的速度优势十分有限，且在优化阶段可以很方便的实现这一优化，因此转而使用新设计。

输出信息

旧设计中：对于printf("aaa %d bbb", x)这种情况，解决方法为先输出aaa，然后处理x，得到其值后输出，然后输出bbb。 这样的设计会引入bug，假设%d对应的是一个函数，在函数处理过程中也涉及到了输出，那么输出的顺序就错了，应该处理完函数之后，一次性将本次信息全部输出了。

在新设计中，在输出str的时候，引入一个栈来存储需要输出的信息，处理完所有%d对应的exp之后，一次性输出所有需要输出的信息。

七、代码优化设计

本次优化仅仅实现了乘除2的整次幂时的优化。

当求$a*b$，且$b = 2^i$时，变为$a<<i$。

当求$a/b$， 且$b=2^i$时，变为$a>>i$。