[Algorithm] 삽입 정렬

CS Deep Dive/Algorithm/삽입 정렬(Insertion Sort).md

@@ -4,35 +4,31 @@
 
 ![image](https://raw.githubusercontent.com/GimunLee/tech-refrigerator/master/Algorithm/resources/insertion-sort-001.gif)
 
-### **시간 복잡도** 
-
-**최악** 의 경우(역으로 정렬되어 있을 경우) 선택정렬과 마찬가지로, (n-1) + (n-2) + .... + 2 + 1 => n(n-1)/2 즉, O(n^2) 이다.
-
-모두 정렬이 되어있는 경우(Optimal)한 경우, 한번씩 밖에 비교를 안하므로 O(n) 의 시간복잡도를 가지게 된다.  
-또한, 이미 정렬되어 있는 배열에 자료를 하나씩 삽입/제거하는 경우에는, 현실적으로 최고의 정렬 알고리즘이 되는데, 탐색을 제외한 오버헤드가 매우 적기 때문이다.
-
-최선의 경우는 **O(n)** 의 시간복잡도를 갖고, 평균과 최악의 경우 **O(n^2)** 의 시간복잡도를 갖게 된다.
 
+### **예제** 
 
-### **공간 복잡도** 
-주어진 배열 안에서 교환(swap)을 통해, 정렬이 수행되므로 O(n) 이다.
-
-### **장점** 
-- 알고리즘이 단순하다.
-
-- 대부분의 원소가 이미 정렬되어 있는 경우, 매우 효율적일 수 있다.
+![image](https://github.com/jaminleee/tech-interview-study/assets/91969458/670ebc52-4a54-4b01-8180-182c5d25c69b)
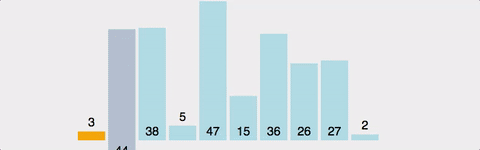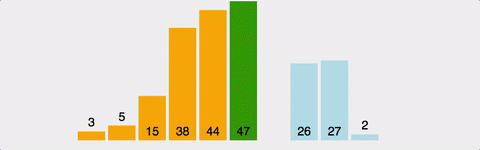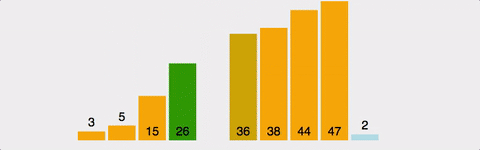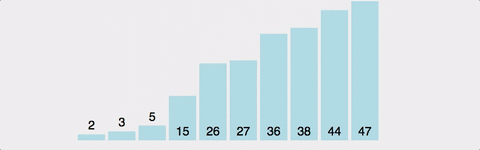
+- 배열에 [372514]가 저장되어 있다</br>
 
-- 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다. => 제자리 정렬(in-place sorting)
-
-- 안정 정렬(Stable Sort) 이다.
-
-- 선택정렬과 같은 O(n^2) 알고리즘에 비교해서 상대적으로 빠르다.
-
-### **단점** 
-
-- 최악, 평균일때 시간복잡도가 O(n^2)으로, 비효율적이다.
+- 1회전: 두 번째 자료인 7이 Key 값이 됨
+	- 7과 첫 번째 자리의 3을 비교. 7이 3보다 크므로 두 번째 자리에 7, 첫 번째 자리에 3을 저장
+
+ - 2회전: 세 번째 자료인 2가 Key 값이 됨
+ 	- 2와 두 번째 자리인 7을 비교. 7이 2보다 크므로 세 번째 자리에 저장
+  	- 2와 첫 번째 자료인 3을 비교. 3이 2보다 크므로 두 번째 자리에 3, 첫 번째 자리에 2를 저장
+- 3회전: 네 번째 자료인 5가 Key 값이 됨
+     	- 5와 세 번째 자리인 7을 비교. 7이 5보다 크므로 네 번째 자리에 저장
+     	- 5와 두 번째 자리인 3을 비교. 5가 3보다 크므로 세 번째 자리에 5, 두 번째 자리에 3을 저장
+- 4회전: 다섯번째 자료인 1이 Key 값이 됨
+  	- 1과 네 번째 자리인 7을 비교. 7이 1보다 크므로 다섯번째 자리에 저장
+  	- 1과 세 번째 자리인 5를 비교. 5가 1보다 크므로 네 번째 자리에 저장
+  	- 1과 두 번째 자리인 3을 비교. 3이 1보다 크므로 세 번째 자리에 저장
+  	- 1과 첫 번쨰 자리인 2를 비교. 2가 1보다 크므로 두 번째 자리에 저장
+- 5회전: 여섯번째 자료인 4가 Key 값이 됨
+   	- 4와 다섯번째 자리인 7을 비교. 7이 4보다 크므로 여섯번째 자리에 저장
+   	- 4와 네 번째 자리인 5를 비교. 5가 4보다 크므로 다섯번째 자리에 저장
+   	- 4와 세 번째 자리인 3을 비교. 4가 3보다 크므로 네 번째 자리에 저장.
 
-- 길이가 길어질수록 비효율적이다.
 
 ### **구현 코드** 
 
@@ -85,4 +81,50 @@ public class Insertion_Sort {
 
 	}
 }
-```
+```
+**[Python]**  
+
+```python
+
+def insert_sort(x):
+	for i in range(1, len(x)):
+		j = i - 1
+		key = x[i]
+		while x[j] > key and j >= 0:
+			x[j+1] = x[j]
+			j = j - 1
+		x[j+1] = key
+	return x
+
+
+```
+### **시간 복잡도** 
+
+**최악** 의 경우(역으로 정렬되어 있을 경우) 선택정렬과 마찬가지로, (n-1) + (n-2) + .... + 2 + 1 => n(n-1)/2 즉, O(n^2) 이다.
+
+모두 정렬이 되어있는 경우(Optimal)한 경우, 한번씩 밖에 비교를 안하므로 O(n) 의 시간복잡도를 가지게 된다.  
+또한, 이미 정렬되어 있는 배열에 자료를 하나씩 삽입/제거하는 경우에는, 현실적으로 최고의 정렬 알고리즘이 되는데, 탐색을 제외한 오버헤드가 매우 적기 때문이다.
+
+최선의 경우는 **O(n)** 의 시간복잡도를 갖고, 평균과 최악의 경우 **O(n^2)** 의 시간복잡도를 갖게 된다.
+
+
+### **공간 복잡도** 
+주어진 배열 안에서 교환(swap)을 통해, 정렬이 수행되므로 O(n) 이다.
+
+### **장점** 
+- 알고리즘이 단순하다.
+
+- 대부분의 원소가 이미 정렬되어 있는 경우, 매우 효율적일 수 있다.
+
+- 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다. => 제자리 정렬(in-place sorting)
+
+- 안정 정렬(Stable Sort) 이다.
+
+- 선택정렬과 같은 O(n^2) 알고리즘에 비교해서 상대적으로 빠르다.
+
+### **단점** 
+
+- 최악, 평균일때 시간복잡도가 O(n^2)으로, 비효율적이다.
+
+- 길이가 길어질수록 비효율적이다.
+