-
Notifications
You must be signed in to change notification settings - Fork 448
New segmented sort algorithm #357
New segmented sort algorithm #357
Conversation
e24e68f to
89f587c
Compare
|
Hi, do we know how much this PR will benefit well-balanced segmented sort with a small number of segments? For example, 1 -256 segment, 120000 elements in each segment. |
Hello, @zasdfgbnm! There should be no significant speedup in this case. The modern GPU version of the segmented sort might perform better in the case of very few large segments. But its speedup doesn't scale well in the range of segments that you've mentioned. |
|
@senior-zero Noted, thanks for the info! |
|
DVS: 30309327 |
There was a problem hiding this comment.
Choose a reason for hiding this comment
The reason will be displayed to describe this comment to others. Learn more.
Really happy to see this patch! These speedups are incredible.
Questions related to the PR description:
- In the speedup plots for segment size vs. number, which axis is which?
- Why were WarpLoad/Store needed? Could they be replaced with a strided thread load?
Should WarpExchange be WarpShuffle (to match existing BlockShuffle)?(I forgot aboutBlockExchangeand the existing convention, ignore this :P)- How long does it take to compile this implementation compared to the current implementation with the same inputs? What about binary size?
- When describing the single-kernel approach, does "CTA number" refer to "current CTA index" or "number of CTAs"?
- In the speedup plot comparing LRB to partitioning, can you describe the input a bit more? How big were the segments? Were they uniformly sized? How many segments in total? Is "matrix id" the number of segments?
- Same questions as above about the speedup plot comparing this PR to
DeviceSegmentedRadixSort.
Note that I haven't reviewed the code yet, so some of the these may be answered in the patch. Feel free to just point out the relevant code when relevant. I'll post another review of the code soon.
Y-axis represents segment size. X-axis represents the numbers of segments in the form 1 << (14 + x).
In some combinations of GPU architecture +
It's about six times slower to compile the new version. The binary size is about 5 times larger.
It's the current CTA index.
"To benchmark the new algorithm on real-world data, I've converted sparse matrices collection to segment sizes. Segments number is equal to the number of rows in a sparse matrix, while segment size is equal to the number of non-zero values in this row." So the matrix id is just an identifier of a sparse matrix that was converted to segment sizes. The maximal number of segments was |
I've removed all the policies except one for both |
Nice, that's much better than 5-6x :) This will be further improved by the if-target branch when it lands. |
30ff59c to
75b194c
Compare
|
@allisonvacanti, thank you for your comments! I've addressed them in the "Fix review notes" commit and also rebased this branch. I'm looking forward to your opinion on these changes. |
31a6a68 to
07cf600
Compare
|
DVS CL: 30537984 |
92e130a to
7ba073c
Compare
d03cd6b to
1072b8c
Compare
3c1a793 to
8a70d82
Compare

This PR includes a new segmented sort facility. Few approaches to this problem exist.
Embed segment number into keys
This approach provides an elegant solution to the load-balancing issue but can lead to slowdowns. It also can't be applicable if the number of bites representing segments number exceeds a maximal number of bytes used by keys.
Modified merge sort approach
This idea is implemented in modern GPU. I've used this approach as a reference for comparison with the new segmented sort algorithm. As I show below, this approach can be outperformed in most cases.
Kernel specialisation
The idea behind this approach is to partition input segments into size groups. Specialised kernels can further process each size group. The LRB approach initially discussed in the issue falls into this category. It also represents the approach that the new segmented sort algorithm relies on.
I'm going to briefly describe the genesis of the new segmented sort algorithm to justify some design decisions.
To minimise the number of kernel specialisations, I've benchmarked different approaches to small (under a few hundred items) segment sorting. I've benchmarked single-thread even-odd sorting, bitonic warp sorting and newly added warp merge sort. The warp-scope merge-sort approach demonstrated some advantages: it can sort bigger segments and outperforms other methods (in the majority of cases).
Warp-scope merge sort is included in this PR as a separate facility. It's possible to partition architectural warp into multiple virtual ones to sort multiple segments simultaneously. The warp-scope merge sort duplicated a significant part of the previously introduced block-scope merge sort, so I extracted the merge-sort strategy into a separate facility. Both warp and block sort share this strategy.
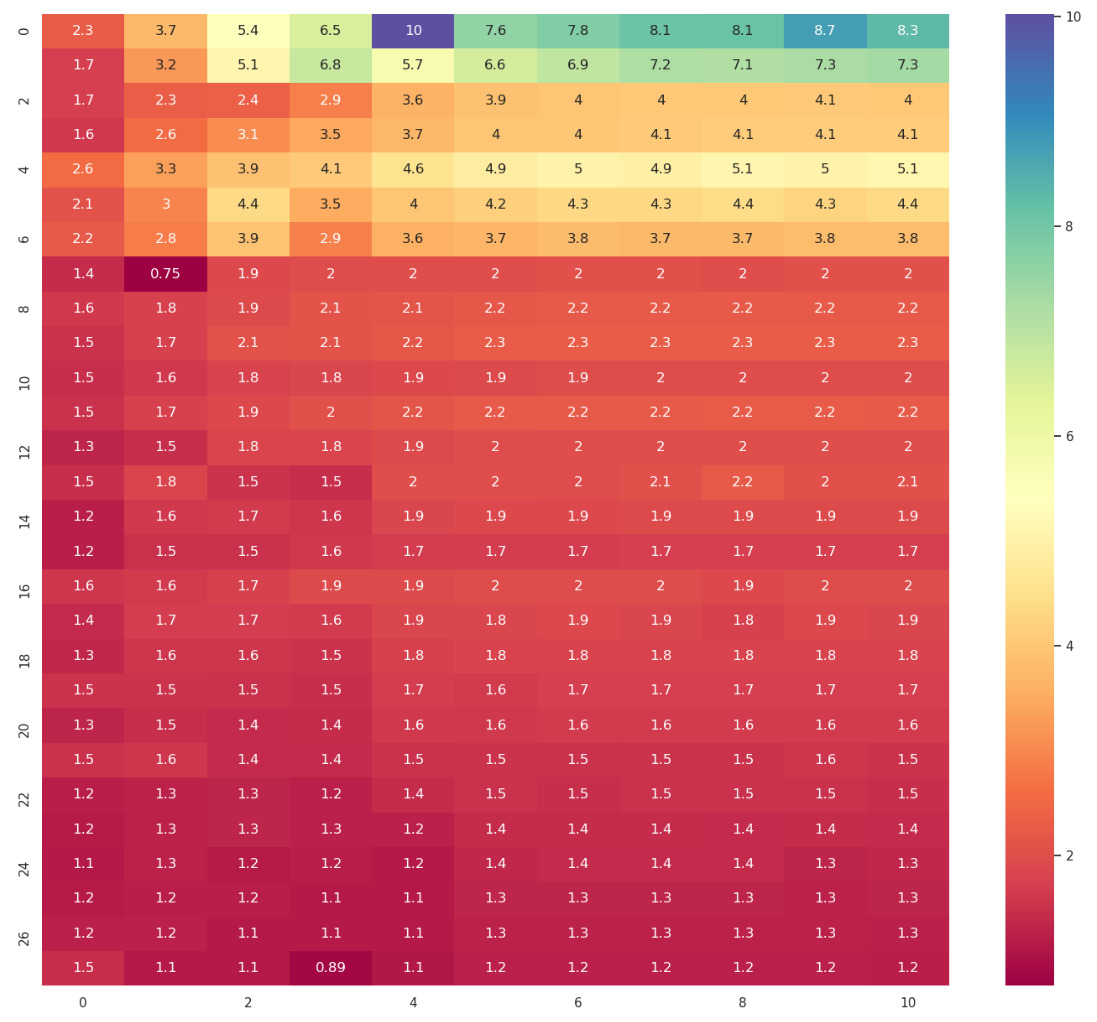
Here's the speedup of warp-scope merge sort over warp-bitonic sort:
And the speedup of warp-scope merge sort over single-thread odd-even sort:
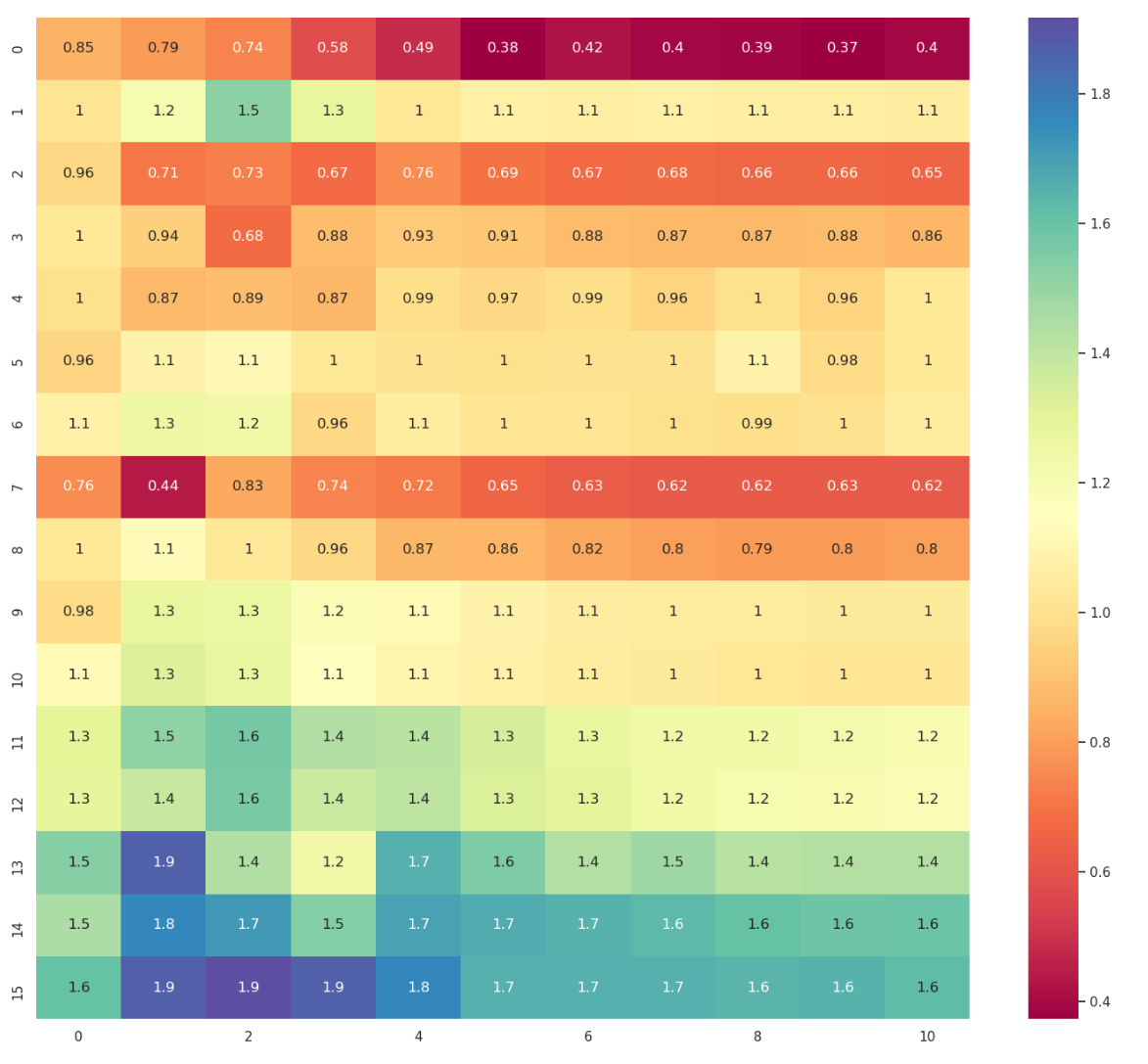
In the figures above I vary segment sizes and segments number.
To further increase the performance of warp-scope merge sort I needed to load and store data efficiently. I needed warp-scope load, store and exchange facilities. These facilities are also provided in this PR.
Using a proper sorting algorithm was not enough. Initially, I've assigned a CUDA thread block to a segment. Although this approach demonstrated speedup over the existing one, it led to inefficient resource utilisation because most threads were idle. Nonetheless, a kernel like this is used as a fallback solution when there are not enough segments. If idle threads don't block other CTAs from execution, there's no reason to spend time on segments partitioning. The fallback kernel helped to eliminate cases when the partitioning stage led to the overall slowdown of the new algorithm.
Initially, I implemented a single kernel for all size groups. Depending on the CTA number, I allocated a different number of threads per segment. That is, if the segment size exceeded a few thousand items, I've used slow block-scope radix sort. If the data was about a thousand items and fit into shared memory, I've used in-shared-memory block-scope radix sort. In all these cases, the whole CTA was assigned to a single segment. If the CTA number exceeded the number of large segments, I've partitioned CTA into multiple warp groups, each processing a separate segment. It happened that the large-segment branch limited the occupancy of small-segment one. So I separated this kernel into two. One kernel processes large segments and contains two branches - in-shared-memory sort and slow block-scope sort. Another kernel processes medium and small segments.
To overlap small/large segments processing, I've used concurrent kernels. This PR contains a single-stream implementation, though. The multi-stream API is out of the scope of this PR and might be introduced later.
Segments partitioning
The LRB approach discussed in the initial issue balances segments in a non-deterministic way. In some cases, it led to slowdowns because consecutive sub-warps might not end up processing consecutive segments. Here's the speedup of the LRB approach compared to the partitioning based approach.
I've tried applying LRB only to the large segments group. This approach also leads to controversial performance results. In rare cases, when an extremely large segment is located in the tail of the large segments group, LRB leads to performance improvements. Otherwise, there are enough segments to overlap its processing, and the LRB stage leads to slowdowns. Therefore, we decided to opt-in LRB. The API with pre-partitioned segments is going to be implemented later. Here's the speedup of the version where I apply LRB to the large segment group.
Instead of LRB, I've implemented a three-way partition facility, which is included in this PR. It leads to deterministic partitioning of segments and might be used outside of the segmented sort. The three-way partitioning stage is faster than the LRB stage.
Temporary storage layout
The temporary storage layout of the new segmented sort is quite complex. To simplify the code and make it safer, I've introduced temporary storage layout wrappers, which can be found in this PR.
Performance
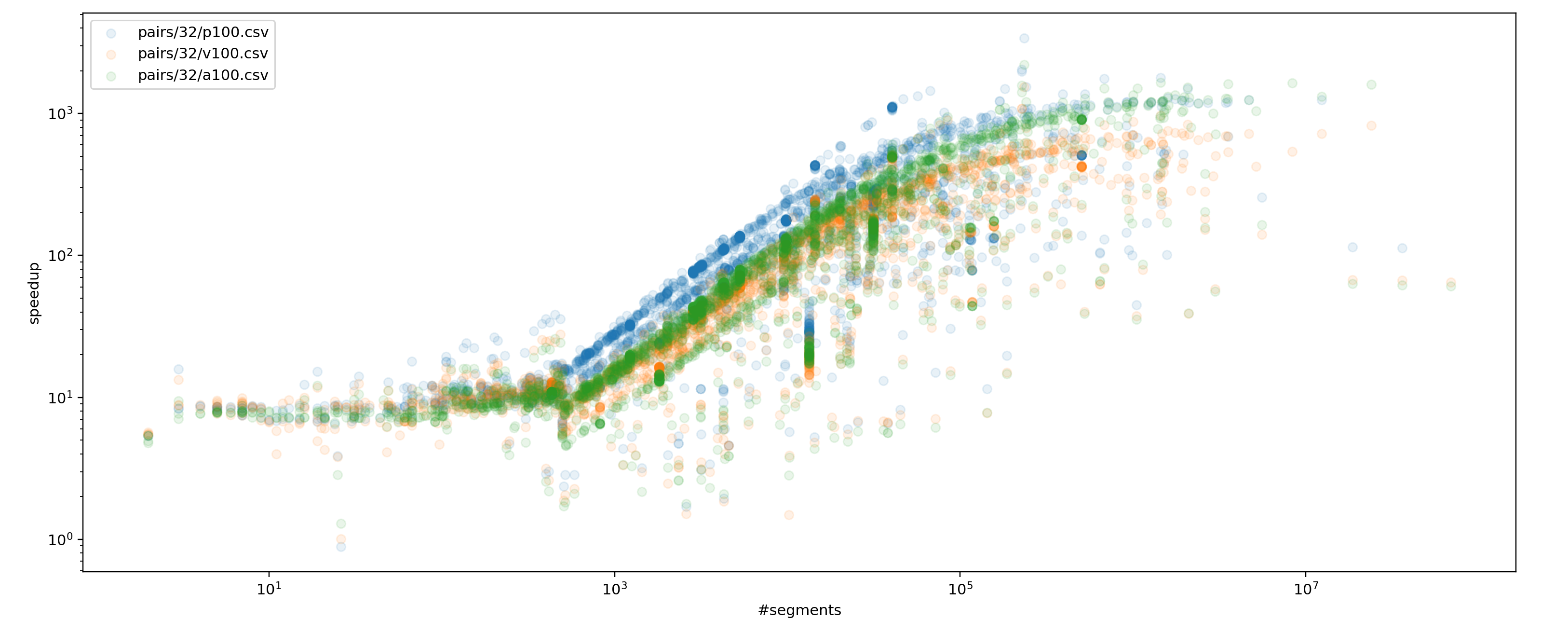
To benchmark the new algorithm on real-world data, I've converted sparse matrices collection to segment sizes. Segments number is equal to the number of rows in a sparse matrix, while segment size is equal to the number of non-zero values in this row. Here's the speedup of the new algorithm compared to the
cub::DeviceSegmentedRadixSorton A100 GPU while sorting pairs ofstd::uint32_tandstd::uint64_t.The speedup depends on the segments number: