-
Notifications
You must be signed in to change notification settings - Fork 349
SQL Performance Enhancement:Binary Flag
[Abstract]
The essay analyzes the fundamental reason behind slow SQL statements and provides the solution to make improvements through code samples.
We call the data, which is used to identify whether a certain flag is “YES or NO”, binary flag. The binary flags can be stored as the boolean field of data table when there are not many of them, only from a few to dozens.
For example, table T contains fields of id, flag1, flag2, ..., flag N and many other fields, among which field flagi is a “YES or NO” flag stored as a boolean field. The SQL writes like follows concerning the calculation on binary flag:
select … from T where flag2 and flag18 and flag25 and …
The database first filters the data whose second binary flag (referred to as flag2), flag8 and flag25 are all “YES” and meanwhile the data satisfy other conditions, and then performs further calculation.
In practice, the number of binary flags can amount to hundreds or even thousands and keep increasing dynamically. The database table cannot support thousands of columns, so we can not store so many binary flags in one table and can hardly add fields dynamically either. So this is not a feasible method.
The first solution comes to our mind is to store thousands of fields in several tables, for example, every table stores 100 fields, then 20 tables can store 2,000 fields. The involved tables need to be joined with primary key id for calculation, and SQL is as follows:
select … from T1 left join T2 on T1.id = T10.id left join T15 on T1.id=T15.id
where T1.flag2 and T10.flag913 and T15.flag1462 and …
The overall rows of the tables are usually quite big, which needs to be stored on external storage. Performing join operation on several big tables on external storage causes bad performance. In addition, the database generally adopts row-based storage. That is, even only one field participates in the calculation, other hundreds of fields in the current data table have to be traversed as well, which is very time-consuming.
We can also use one field and several records to store the binary flag to avoid JOIN of big tables. For example, table T contains fields of id (number), flag (flag number), and so on. “id” and “flag” constitute composite primary keys, and each “id” corresponds dozens of “flag” as most. There may be thousands of binary flags in number, but only a few of them can actually be used in calculation.
Such a storage scheme can easily handle the increase of flags, and the above SQL should be rewritten as:
select … from T
where (flag=2 or flag=18 or flag=25) and …
group by id
having count(flag)=3
The database first filters the data whose “flag” is 2, 8, or 25 and meanwhile, the data should satisfy other conditions. Then it groups the data by id and filters out the groups with 3 records. Generally speaking, the result set of grouping table T by id tends to be big, and performing big group requires buffering on external storage, which results in bad computation performance.
Also, other field values of the same id are usually identical and become redundant data because of flag, making the gross data enormous. The performance also decreases clearly in this method.
We can store id and other fields in another data table T1. Only id field and flag field are retained in table T to avoid redundancy. These two tables are first joined by id and then calculated. Better universality can also be achieved in this way, and the above SQL should be rewritten as:
select id,… from T t left join T1 t1 on t.id=t1.id
where t.flag in (2,18,25) and …
group by t.id
having count(t.flag)=3
)
However, this method still can’t solve the problem of big group and the JOIN of two big tables, which still results in bad performance.
1. Storage and calculation in bits
To improve the performance, we first need to pre-process the original data, storing the binary flags in bits. A small integer is 16 bits, each bit of which can store a binary flag with 1 representing “YES” binary flag and 0 representing “NO” binary flag. That is, a small integer can store 16 binary flags, and 100 of them can store 1,600 binary flags. We can store hundreds of small integer fields in columnar storage, and the fields include id, f1, f2, ..., fn, ... Small integer field fi contains 16 values of binary flags whose corresponding flag numbers are from (i-1)*16+1 to i*16.
Then we can achieve the binary flags analysis with bit calculation. For example, when flag 2, 18 and 25 are all “YES”, calculating that flag2 corresponds to the second bit of f1 requires to perform “bitwise AND” between f1 and small integer 2. The condition will be satisfied if the result is also 2. This is because small integer 2 is 10 in binary digit, and the result of “bitwise AND” will still be 2 if the second bit of f1 is 1.
Both flag18 and flag25 are larger than 16 and smaller than 32, so they are in the second small integer field f2 and the former corresponds to the second bit of f2, the latter corresponds to the ninth bit. We need to perform “bitwise AND” on f2 and small integer 258 (100000010 in binary digit), and if the result is 258, then the condition will be satisfied. Finally, we perform logical AND on the two results of bitwise AND, and if the result is true, then binary flag condition will be satisfied.
In this method, every id has only one row of data without redundancy and big group. The performance will be much improved with only one traversal of the data. The advantages of storage in bits also include:
1) Only a few binary flags out of hundreds are read due to the small amount of involved binary flags, which makes the most of columnar storage, greatly decreasing the reading amount of data on external storage.
2) Every id corresponds to from a few to dozens of flags in spite of thousands of flags in total. Therefore, the hundreds of small integer fields are relatively sparse in general, which can bring about a higher ratio of compression on columnar storage. The added CPU time for decompressing data can be ignored when further decreasing the reading amount of data on external storage.
2. Data update
In the situation of binary flag, the updating of data is usually the change of flag value. Compression on columar storage can improve performance but cannot modify the compressed data directly. New data have to be regenerated to update, which takes a little longer but ensures the high-performance of flag calculation.
We can write the modified data in an independent data area (referred to as patch area) if the data updating is small and not frequent. We order the patch area data and the ordinary data by primary key (id), and then perform merge algorithm when reading them. Although the patch area has an impact on the performance, it solves the time-consuming issue of the frequent generating of whole data.
The patch area gets bigger and bigger after many times of modifications, thus having a greater impact on performance. Therefore, we should regularly place the patch area data in the ordinary area to rewrite part of the data (starting from the smallest primary key id in the patch area, what before it stays unchanged), and clean up the patch area at the same time.
1. Convert data to be stored in bits.
Suppose the original data are stored in T-original.ctx, which contains id (number), flag (flag number), and other fields. Id and flag constitute the composite primary keys. In practice, the original data may be retrieved from the database. Therefore, the code needs to be modified to retrieve data from a connected database.
| A | B | |
|---|---|---|
| 1 | ="#id,"/to(500).("f"/~).concat@c() | ="id,"/to(500).("f"/~).concat@c() |
| 2 | =to(16).(int(bits(pad@r("1","0",~)))) | =A2.m(16,1:15) |
| 3 | =file("T-original.ctx").open() | =A3.cursor().sortx(id) |
| 4 | =file("T.ctx").create@y(${A1}) | =create(${B1}) |
| 5 | for B3;id | =B4.reset() |
| 6 | =B5.record(A5.id|to(500).(0)) | |
| 7 | =A5.new(int(ceil(~.flag/16)):position,B2(~.flag%16+1):value) | |
| 8 | =B7.group(position;int(or(~.(value))):value) | |
| 9 | =B8.(B4(1).field(~.position+1,~.value)) | |
| 10 | =A4.append(B4.cursor()) | |
| 11 | >A3.close(),A4.close() |
A1, B1: generate the structure of the new composite table and the intermediate table sequence dynamically based on the number of small integer fields:
#id,f1,f2,… ,f500
id,f1,f2,…,f500
The small integer fields are 500 in number, so they can store 8,000 flags.
Here only id and small integer fields are shown. Other field names need to be added when other fields are required, and so does the following calculation, which will not be included here.
A2, B2: generate the “bit storage conversion table”. This calculation can be omitted here if env() function is used to put it into global variables. The advantages of “bit storage conversion table” to performance will be introduced later.
A3, B3: open the original composite table and sort id on the external storage.
A4, B4: create a new composite table and save the intermediate table sequence.
A5: loop through the cursor of B3 and read data from the cursor every time until id changes. That is, read all the data of one id every time. The first loop is as follows:

B5: clear up the table sequence of B4 to prepare for the bit storage result of the current id.
B6: fill in B4 with the current id and the initial value 0 of f1 to f500, and the result is as follows:

B7: calculate the result is the which bit of which small integer based on the quotient and remainder of flag and 16 in A5 and then search the “bit storage conversion table” B2 with remainder+1 to get the value of the small integer. For example, the value of “flag” is 48, which corresponds to the 16th bit of the third small integer, “position” is 3, the remainder is 0 and “value” is 32768 (1000 0000 0000 0000 in binary digit).
The current loop is traversing the cursor of the original data which is big in amount. The conversion of bit storage will also be enormous if it is calculated in the loop. But we calculate the “bit storage conversion table” in advance and can search the table directly here, which improves the performance greatly.
The result is:

B8: bind the same “position” of the results in B7. For example, flag122 and flag125 are both in the eighth small integer, then “bitwise OR” needs to be performed between these two “value” to bind them as one. And the result is:

B9: set the corresponding small integer of the “position” in table sequence B4 as “value” based on B8. For example, “position” is 3, then the value of f3 should be set as 32768. Execute B4 as follows:

B10: convert B4 as a cursor and append it to the end of T.ctx.
A11: close the two composite tables after the loop.
2. Calculate the data, which are stored in composite table T.ctx in bits, with flag 2, 18 and 25 as “YES”.
A simple code can accomplish the calculation since the data are pre-processed:
=file("T.ctx").open().cursor(id,…;and(f1,2)==2&&and(f2,258)==258&&…)
However, the given parameters are actually a list of flag numbers like “2, 18, 25”, then some code is needed to convert them to the filtering condition of “bitwise AND”. The complete sample is as follows:
| A | B | |
|---|---|---|
| 1 | ="2,18,25" | =A1.split(",").(int(~)) |
| 2 | =to(16).(int(bits(pad@r("1","0",~)))) | =A2.m(16,1:15) |
| 3 | =B1.new(int(ceil(~/16)):position,B2(~%16+1):value) | |
| 4 | =A3.group(position;or(~.(value)):value) | |
| 5 | =A4.("and(f"/position/","/value/")=="/value) | =A5.concat("&&")/"&&…" |
| 6 | =file("T.ctx").open() | =A6.cursor(id,…;${B5}) |
A1: several flag numbers will be the given parameters in practice.
B1: split the flag numbers into a sequence and convert them to integers. The result is:

A2: generate 16 small integers whose first, second, ..., sixteenth bits are 1 and other bits are 0. the result is:
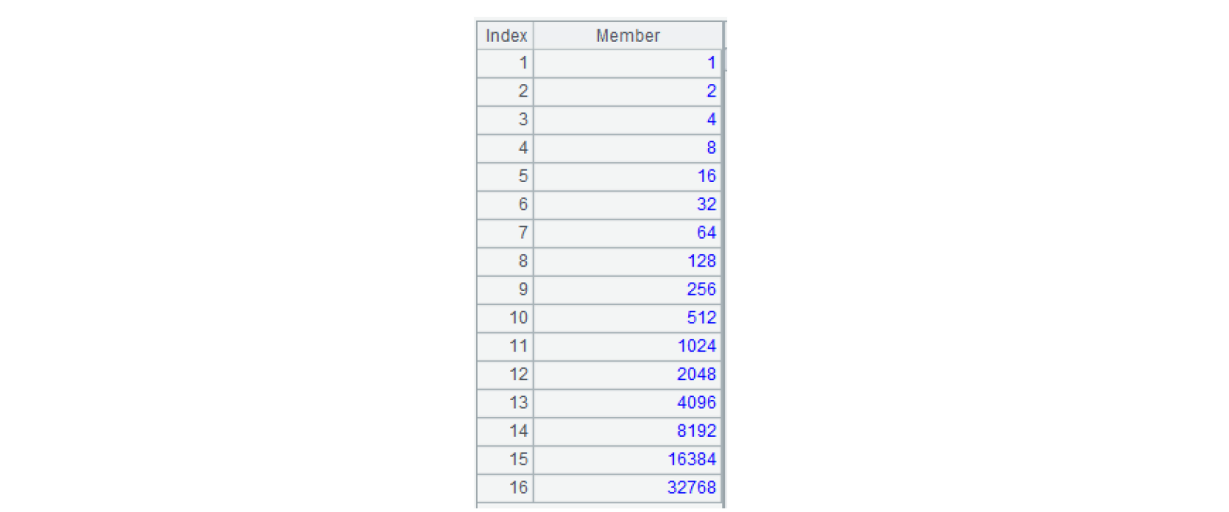
B2: adjust the positions of the members in A2 as follows:

The result of B2 will be repeatedly used in the code of flag calculation and data conversion, and here we call it “bit storage conversion table”. The table can be directly referred if we calculate it in advance when the system is initiated and use the env() function to save it in global variables, which further improves the performance.
B3: calculate the corresponding small integer (position) and the corresponding value in that integer (value) of the flag numbers in B1. For example, divide flag number 18 by 16, the quotient is 1 and the remainder is not 0, then flag 18 corresponds to the second small integer (position is 2); the value of the above corresponding small integer is 2 because of remainder 2 which refers to the third (remainder+1) member of “bit storage conversion table”. The result of B3 is:

B4: bind the same “position”s in the result of B3. For example, flag18 and flag25 are both in the second small integer (position is 2), the value of 18 is 2 (10 in binary digit), and the value of 25 is 256 (1 0000 0000 in binary digit). Perform “bitwise AND” between 2 and 25 to get the final value of the second small integer, that is, 258 (1 0000 0010 in binary digit). The result is:

A5, B5: generate a filtering sequence based on the result of B4, and concatenate it to create a string with &&. The “...” in B5 can be filled in with other filtering conditions. The result is:
and(f1,2)==2&&and(f2,258)==258&&…
A6, B6: open the composite table and create a cursor with filtering conditions based on it. Continue to write the code to complete the counting based on the cursor.
The reading amount is relatively big because the composite table needs to be traversed. The reason why we emphasize on storage in small integer is that SPL is developed in Java and Java is very slow in generating objects. SPL has already generated all the 16 integers (0-65535). New objects will no longer be generated if the read integer is in the above range, which lessens the calculation as well as the occupation of memory.
3. Update data.
We can update the composite table T.ctx instead of recalculating to create a new composite table if the data modification is small and not frequent. The modified data should also be converted to store in bits before the update. The structure of update.btx, where the converted data are stored, is supposed to be the same as that of T.ctx.
| A | B | |
|---|---|---|
| 1 | =file("update.btx").import@b() | |
| 2 | =file("T.ctx").open() | =A2.update(A1) |
A1: read the modified data and store all of them in memory if the modification volume is not big.
A2: open the composite table.
B2: update the composite table and write the data in patch area.
The code to clean up the patch area regularly is as follows:
| A | B | |
|---|---|---|
| 1 | =file("T.ctx").open() | |
| 2 | if (day(now()))==1 | =A1.reset() |
A1: open the composite table.
A2: identify whether the current date is day 1, if so, execute B2. This code does the cleaning once a month, and other identification can be adapted to different time cycles.
B2: reset the composite table quickly to place the patch area in the column area.
SPL Resource: SPL Official Website | SPL Blog | Download esProc SPL | SPL Source Code